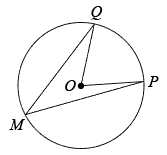
①;
(填“>”,“=”,“<”)
②将D点绕点B顺时针旋转60°得到点E,则线段DB,DC,DA的关系为.
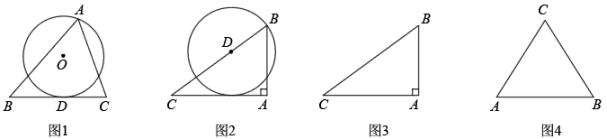
①如图2,当点与点
重合时,求半圆
在
上截得的线段
的长;
②将半圆移动到如图2所示的位置时作为初始位置,将线段
连带半圆
按顺时针方向开始旋转,如图3所示,设旋转角为
. 当半圆
与
的边相切时,直接写出点
运动的路径长.(注:结果保留
,
,
)
直线
;
直线
;
双曲线
, 是
的关联图形的是(请直接写出正确的序号).

学习小组中的一位同学进行了如下证明:
如图2,连接 ,
,
∵ ,
.
∴
∵ ,
∴
……
请完成下列的任务:

①矩形;②菱形;③正方形
①求证:四边形ABCD是“婆氏四边形”;
②当AD+BC=4时,求⊙O半径的最小值.


①如图②,已知平面内有一点D, , 试说明点D是
的“直角点”.

②如图③,直线分别与x轴、y轴相交于点A、B,若线段
上所有点都是半径为r的圆的“直角点”,求r的最小值与该圆心的坐标.


证明:如图2,在上截取
, 连接
、
、
和
.

是
的中点,
,
又 ,
,
,
,
又 ,
,
即
.



问题情境:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l,圆心角为的扇形.工人在制作圆锥形物品时,通常要先确定扇形圆心角度数,再度量裁剪材料.

①如图2,若点D在边上,
, 以D为圆心,
长为半径作圆,则
是
的“切接圆”吗?请说明理由.
②在图3中,若点D在的边上,以D为圆心,
长为半径作圆,当
是
的“切接圆”时,求
的半径(直接写出答案).
思维拓展
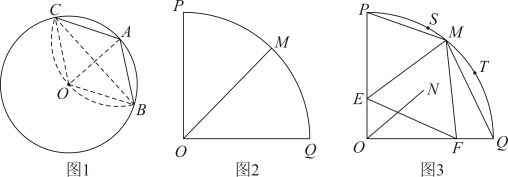
①如图2,当点M是弧中点时,在线段
、
上各找一点E、F,使得
是等边三角形.试用尺规作出
, 不证明,但简要说明作法 , 保留作图痕迹.
②在①的条件下,取的内心N,则
.
③如图3,当M在弧上三等分点S、T之间(包括S、T两点)运动时,经过兴趣小组探究都可以作出一个
是等边三角形,取
的内心N,请问
的长度是否变化.如变化,请说明理由;如不变,请求出
的长度.
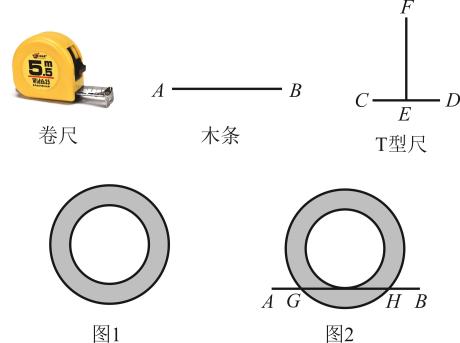
操作:如图1,分别将半圆的圆心角
(
取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);

交流:当时,可以仅用圆规将半圆
的圆心角
所对的弧三等分吗?
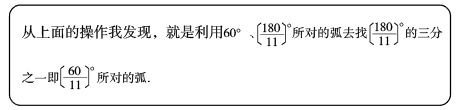
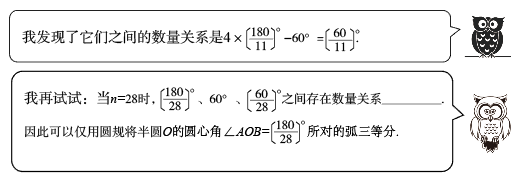
探究:你认为当满足什么条件时,就可以仅用圆规将半圆
的圆心角
所对的弧三等分?说说你的理由.