求:
数学问题:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:( ).现已知商品的进价为每件40元,如何定价才能使每个星期的利润达到6080元,且顾客能够得到更大的实惠?
解:设…,
根据题意,所列出方程:(20﹣x)(300+ ×40)=6080,
…
根据小明所列方程,完成下列任务:
问题:
用“转化”思想求方程 的解.

试猜想与
是否相似?并证明你的猜想.
如图,连接交
于点H,
与
相交于点G,
是否成立?并说明理由.
若 , 直接写出
的值.
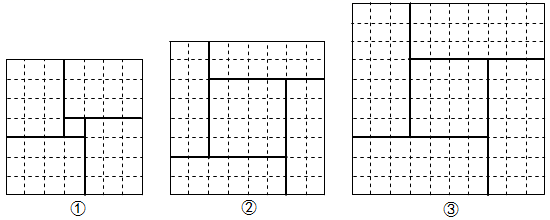
如图①,在平行四边形中,点E是
边的中点,点F是线段
上一点,
的延长线交
于点
. 若
, 求
的值.



在图①中,过点E作交
于点
, 则
的值为,
的值为,
的值为.
如图②,在原题的条件下,若 , 则
的值为(用含
的代数式表示).
如图③,若点F在线段的延长线上,
的延长线交
的延长线于点
,
, 则
的值为(用含n的代数式表示).
如图2,四边形为平行四边形,F在
边上,
, 点E在
延长线上,连接
, 若
,
, 求
的长;
如图3,在中,D是
上一点,连接
, 点E、F分别在
、
上,连接
, 若
,
,
,
;求
的值.
和
的位置关系是,
和
的数量关系是.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则 .
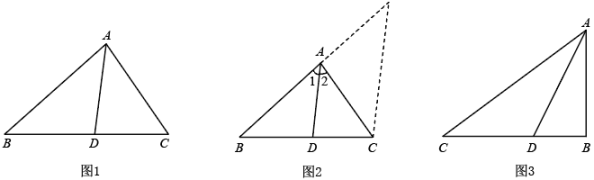
下面是这个定理的部分证明过程.
证明:如图2,过点C作 . 交BA的延长线于点E.…
任务:
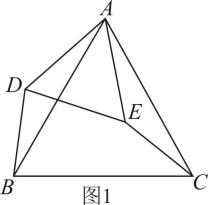
如图2,和
都是等腰直角三角形,
, 连接
. 求
的值.

如图3,和
都是直角三角形,
,
. 连接
, 延长
交
于点F,连接
. 若
恰好等于
, 请直接写出此时
之间的数量关系.


探究一:已知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍?如图,假设存在正方形EFGH,它的面积是正方形ABCD的2倍.
因为正方形ABCD的面积为1,则正方形EFGH的面积为2,
所以EF=FG=GH=HE= , 设EB=x,则BF=
﹣x,
∵Rt△AEB≌Rt△BFC
∴BF=AE=﹣x
在Rt△AEB中,由勾股定理,得
x2+(﹣x)2=12
解得,x1=x2=
∴BE=BF,即点B是EF的中点.
同理,点C,D,A分别是FG,GH,HE的中点.
所以,存在一个外接正方形EFGH,它的面积是正方形ABCD面积的2倍
探究二:已知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的3倍?(仿照上述方法,完成探究过程)
探究三:已知边长为1的正方形ABCD, ▲ 一个外接正方形EFGH,它的面积是正方形ABCD面积的4倍?(填“存在”或“不存在”)
探究四:已知边长为1的正方形ABCD,是否存在一个外接正方形EFGH,它的面积是正方形ABCD面积的n倍?(n>2)(仿照上述方法,完成探究过程)
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则 .

下面是这个定理的部分证明过程.
证明:如图2,过点C作 . 交BA的延长线于点E.…
请按照上面的证明思路,写出该证明过程的剩余部分;
在凸四边形中,若一边与它的两条邻边组成的两个内角相等,则称该四边形为邻等四边形,这条边叫做这个四边形的邻等边.
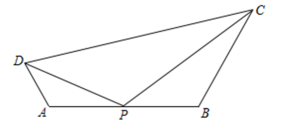


如图13-1,AD为△ABC的角平分线,∠ADC=60°,点E在AB上,AE=AC.求证:DE平分∠ADB.
如图13-2,在(1)的条件下,F为AB上一点,连结FC交AD于点G.若FB=FC,DG=2,CD=3,求BD的长.
如图13-3,在四边形ABCD中,对角线AC平分∠BAD,∠BCA=2∠DCA,点E在AC上,∠EDC=∠ABC.若BC=5,CD=2 ,AD=2AE,求AC的长.

如图2,在Rt△ABC中,∠ACB=90°,AB=10cm , AC=8cm , ∠ACB的平分线交AB于点P , 过点P分别作PE⊥AC , PF⊥BC , 垂足分别为E , F , 求四边形PECF的面积.请写出解答过程.
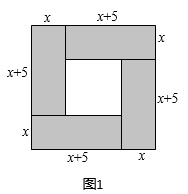
人类对一元二次方程的研究经历了漫长的岁月.一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中.到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明.我国古代三国时期的数学家赵爽也给出了类似的几何解法.赵爽在其所著的《勾股圆方图注》中记载了解方程 即
得方法.首先构造了如图1所示得图形,图中的大正方形面积是
,其中四个全等的小矩形面积分别为
,中间的小正方形面积为
,所以大正方形的面积又可表示为
,据此易得
.

任务:
请阅读下列材料,并完成相应的任务:
阿尔·花拉子米(约780~约850) ,著名阿拉伯数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”。他利用正方形图形巧妙解出了一元二次方程x2+2x-35=0的一个解.将边长为x的正方形和边长为1的正方形,外加两个长方形,长为x,宽为1,拼合在一起面积就是x2+2·x×1+12 , 即x2+2x+ 1,而由原方程x2+2x-35=0变形得x2+2x+1=35+1,即边长为x+1的正方形面积为36.所以(x+1)2=36,则x=5.
任务:
问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:
已知,在菱形ABCD中,BD为对角线, ,AB=4,将菱形ABCD绕顶点A顺时针旋转,旋转角为
(单位°).旋转后的菱形为
.在旋转探究活动中提出下列问题,请你帮他们解决.


