看图填空:已知如图,于D,
于G,
平分
, 求证:
.
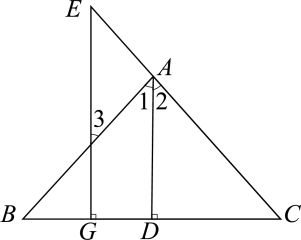
证明:∵于D,
于G( ),
∴ ,
( ).
∴( ).
∴( ).
∴ ▲ ( ),
▲ ( ).
又∵平分
(已知),
∴( ),
∴( ).

证明:∵∠1=∠A,
∴AB ▲ ( ),
∴∠2= ▲ ( ).
∵∠ACB+ ▲ + ▲ =180°,
∴∠A+∠B+∠ACB=180°.
已知:如图, ,
, 求证:
.

证明:∵(已知)
且( ),
∴(等量代换).
∴ ▲ (同位角相等,两直线平行).
∴( ).
∵(已知),
∴( ).
∴ ▲ (两直线平行,内错角相等).
∴(等量代换).

求证: .
证明:∵(已知)
( ),
∴( ),
∴ ▲ ▲ (同位角相等,两直线平行),
∴ ▲ (两直线平行,同位角相等)
又∵(已知),
∴( ),
∴(等量代换).
如图,已知 , 求证
,

证明:∵(已知),
又∵ , ( )
∴ ▲ ,( )
∴ , ( )
∴ ▲ ,( )
∵ , ( )
∴ , ( )
∴ ▲ ,(同位角相等,两直线平行),
∴( )

证明:∵ABCD(已知)
∴ ▲ (两直线平行,内错角相等)
∵(已知)
∴(等量代换)
∴BC ▲ (同旁内角互补,两直线平行)
∴ ▲ ( )
∵ ▲ (对顶角相等.)
∴(等量代换)
解:∵ (已知),

∴ (两直线平行,内错角相等)
又∵ ,
(已知),
∴ (等式的性质).
∴( )
∴( )
∴( )
∴




|
刹车时车速(km/h) |
0 |
10 |
20 |
30 |
40 |
50 |
… |
|
刹车距离(m) |
0 |
2.5 |
5 |
7.5 |
10 |
12.5 |
… |




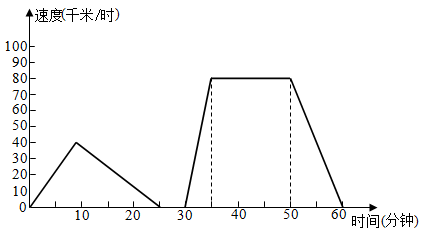
根据图象回答下列问题:
|
时间 |
|
|
|
|
|
|
|
|
|
等待检测人数 |
|
|
|
|
|
|
|
|
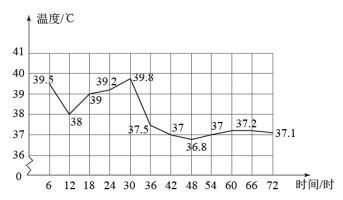
医务人员已检测的总人数(人)与时间(分钟)之间的关系如图所示: