 B .
B . 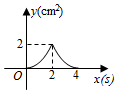 C .
C . 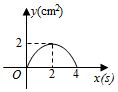 D .
D . 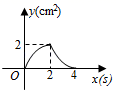
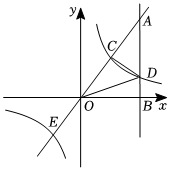
①双曲线的解析式为;②
点的坐标是
;③
;④
. 其中正确的结论有( )
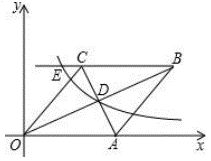

①AE垂直平分DM;②PM+PN的最小值为3;③CF2=GE•AE;④S△ADM=6
.
其中正确的是( )

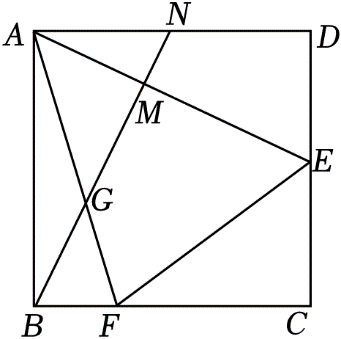
①DE+BF=EF②BN⊥AE③BF=④S△BGF=
中正确的是( )
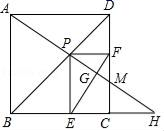





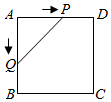
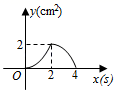
①若动点运动到边
的中点处时,
的面积为.
②在动点的整个运动过程中,
面积的最大值为.
①如图1,若点在线段
上,则线段
与
之间的数量关系是 ▲ , 位置关系是 ▲ ;
②如图2,若点在线段
的延长线上,①中的结论还成立吗?如果成立,请给予证明;如果不成立,请说明理由;
①当t为何值时,四边形的面积等于
?
②当t的值为 时,以B , P , Q三点为顶点的三角形与相似.

①求证:四边形ABEG是“神奇四边形”;
②如图2,点M、N、P、Q分别是AB、AG、GE、EB的中点.试判断四边形MNPQ是不是“神奇四边形”;
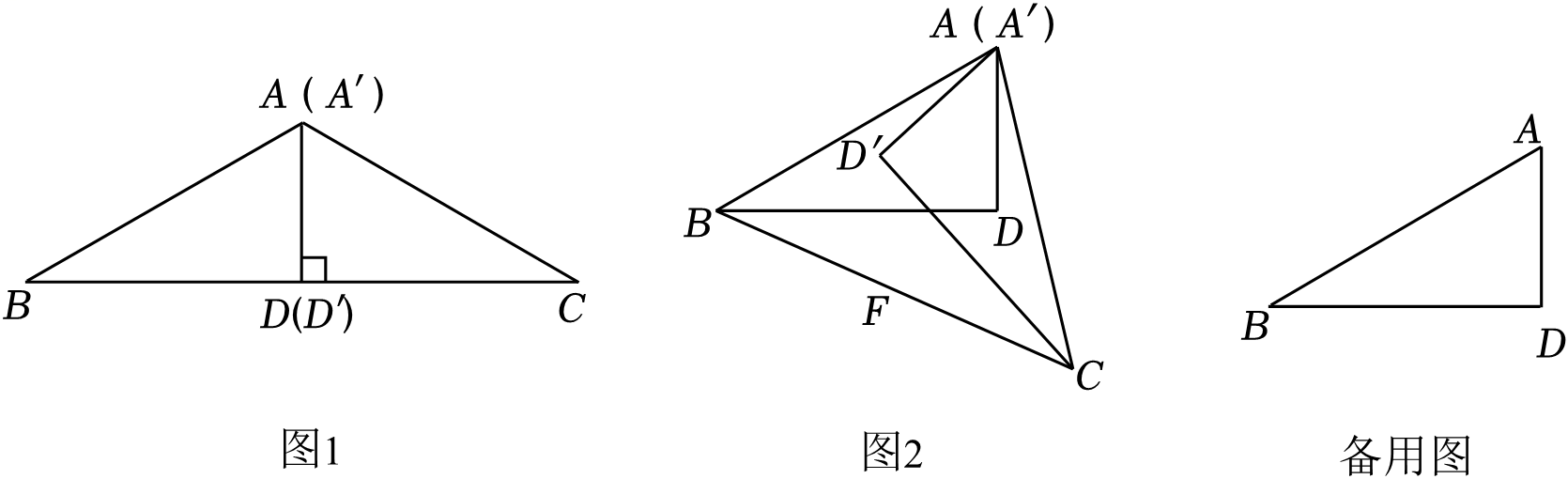
在综合实践活动课上,李老师让同桌两位同学用相同的两块含30°的三角板开展数学探究活动,两块三角板分别记作△ADB和△A'D'C,∠ADB=∠A'D'C=90°,∠B=∠C=30°,设AB=2.
【操作探究】
如图1,先将△ADB和△A'D'C的边AD、A'D'重合,再将△A'D'C绕着点A按顺时针方向旋转,旋转角为α(0°≤α≤360°),旋转过程中△ADB保持不动,连接BC.
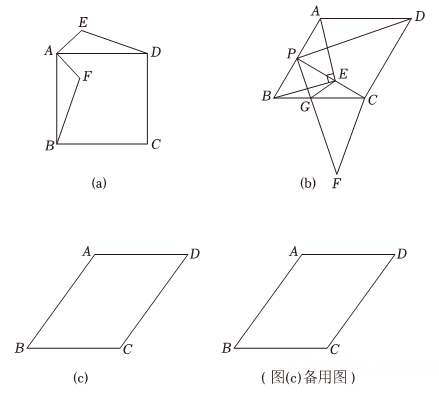
如图(a),E是正方形ABCD外一点,将线段AE绕点A顺时针旋转得到AF , 连接DE , BF . 求证:
;
如图(b),在菱形ABCD中, , P是AB的中点,将线段PA , PD分别绕点P顺时针旋转
得到PE , PF , PF交BC于点G , 连接CE , CF , 求四边形CEGF的面积:
如图(c),在平行四边形ABCD中,为锐角且满足
. P是射线BA上一动点,点C , D同时绕点P顺时针旋转
得到点
,
, 当
为直角三角形时,直接写出BP的长.
以下是两名同学通过不同的方法构造全等三角形来解决问题的思路,
①小聪:过点作
的延长线的垂线;
②小明:在上截取
, 使得
;
请你选择其中一名同学的解题思路,写出完整的解答过程.
在一次综合实践活动课上,王老师给每位同学各发了一张正方形纸片,请同学们思考如何仅通过折纸的方法来确定正方形一边上的一个三等分点.


【操作探究】
“乘风”小组的同学经过一番思考和讨论交流后,进行了如下操作:
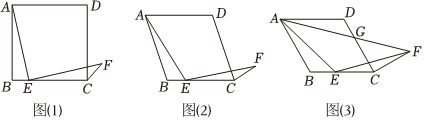
第1步:如图1所示,先将正方形纸片ABCD对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:将BC边沿CE翻折到GC的位置;
第3步:延长EG交AD于点H,则点H为AD边的三等分点.
证明过程如下:连接CH, ∵正方形ABCD沿CE折叠, ∴∠D=∠B=∠CGH=90°, ① , 又∵CH=CH ∴△CGH≌△CDH, ∴GH=DH. 由题意可知E是AB的中点,设AB=6(个单位),DH=x,则AE=BE=EG=3, 在Rt△AEH中,可列方程: ② , (方程不要求化简)解得:DH= ③ , 即H是AD边的三等分点. |
“破浪”小组是这样操作的:
第1步:如图2所示,先将正方形纸片对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:再将正方形纸片对折,使点B与点D重合,再展开铺平,折痕为AC,沿DE翻折得折痕DE交AC于点G;
第3步:过点G折叠正方形纸片ABCD,使折痕MNIIAD.
【过程思考】