题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

2024年中考数学热点探究二十五项目学习

更新时间：2024-04-27 浏览次数：107 类型：二轮复习

一、实践探究题

1. (2023九上·长清期中) 某校项目式学习小组开展项目活动，过程如下：

项目主题：测量旗杆高度

问题驱动：能利用哪些科学原理来测量旗杆的高度？

组内探究：由于旗杆较高，需要借助一些工具来测量，比如自制的直角三角形硬纸板，标杆，镜子，甚至还可以利用无人机…确定方法后，先画出测量示意图，然后实地进行测量，并得到具体数据，从而计算旗杆的高度．

成果展示：下面是同学们进行交流展示时的部分测量方案：

	方案一		方案二		…
测量工具	标杆，皮尺		自制直角三角板硬纸板，皮尺		…
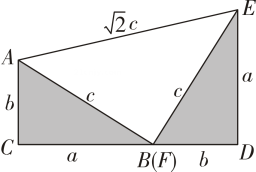
测量示意图	说明：线段AB表示学校旗杆，小明的眼睛到地面的距离CD＝1.7m，测点F与B，D在同一水平直线上，D，F，B之间的距离都可以直接测得，且A，B，C，D，E，F都在同一竖直平面内，点A，C，E三点在同一直线上．		说明：线段AB表示旗杆，小明的身高CD＝1.7m，测点D与B在同一水平直线上，D，B之间的距离可以直接测得，且A，B，C，D，E，F，G都在同一竖直平面内，点A，C，E三点在同一直线上，点C，F，G三点在同一直线上．
测量数据	B，D之间的距离	16.8m	B，D之间的距离	16.8m	…
	D，F之间的距离	1.35m	EF的长度	0.50m	…
	EF的长度	2.60m	CE的长度	0.75m	…
…	…

根据上述方案及数据，请你选择一个方案，求出学校旗杆AB的高度．（结果精确到0.1m）；

答案解析收藏纠错 + 选题

2. (2023九上·滨江月考) 根据以下素材，探索完成任务．

如何设计喷泉喷头的升降方案？

素材1

如图，某景观公园内人工湖里有一个可垂直升降的喷泉，喷出的水柱呈抛物线．记水柱上某一点到喷头的水平距离为x米，到湖面的垂直高度为y米．当喷头位于起始位置时，测量得x与y的四组数据如下：

x（米）	0	2	3	4
y（米）	1	2	1.75	1

素材2

公园想设立新的游玩项目，通过升降喷头，使游船能从水柱下方通过，如图，为避免游船被喷泉淋到，要求游船从水柱下方中间通过时，顶棚上任意一点到水柱的竖直距离均不小于0.4米．已知游船顶棚宽度为2.8米，顶棚到湖面的高度为2米．

问题解决：

（1）任务1：确定喷泉形状
结合素材1，求y关于x的表达式．
（2）任务2：探究喷头升降方案
为使游船按素材2要求顺利通过，求喷头距离湖面高度的最小值．

答案解析收藏纠错 + 选题

3. (2023九下·青秀月考) 某“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制订了测量方案，并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差，小组在测最仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表（不完整）.

课题	测量旗杆的高度
成员	组长××× 组员：×××，×××，×××
测量工具	测量角度的仪器、皮尺等
测量示意图	说明：线段 $\text{[math]}$ 表示学校旗杆，测量角度的仪器的高度 $\text{[math]}$ ，测点A，B与H在同一条水平直线上，A，B之间的距离可以直接测得，且点G，H，A，B，C，D都在同一竖直平面内.点C，D，E在同一条直线上，点E在 $\text{[math]}$ 上.
	测量项目	第一次	第二次	平均值
测量数据	$\text{[math]}$ 的度数	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
	$\text{[math]}$ 的度数	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
	A，B之间的距离	$\text{[math]}$	$\text{[math]}$

任务一：两次测量，A，B之间的距离的平均值是 ▲ m.

任务二：根据以上测量结果，请你帮助该“综合与实践”小组求出学校旗杆 $\text{[math]}$ 的高度.

（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

任务三：该“综合与实践”小组在制订方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳，你认为其原因可能是什么？

答案解析收藏纠错 + 选题

4. (2204九下·温州月考) 根据以下素材，探索完成任务

如何调整足球的发球方向
素材1	如图是某足球场的一部分，球门宽DE=CF=7m，高CD=EF=2.5m，小梅站在A处向门柱CD一侧发球，点A正对门柱CD(即AC⊥CF)，AC=24m，足球运动的路线是抛物线的一部分.
素材2	如图，当足球运动到最高点 $\text{[math]}$ 时，高度为4.5m，即 $\text{[math]}$ ，此时水平距离 $\text{[math]}$ ，以点 $\text{[math]}$ 为原点，直线BA为 $\text{[math]}$ 轴，建立平面直角坐标系.
素材3	距离球门正前方6m处放置一块矩形拦网HGMN，拦网面垂直于地面，且GH∥CF，拦网高HN=4m.
问题解决
任务1	结合素材1，2，求足球运动的高度 $\text{[math]}$ 与水平距离 $\text{[math]}$ 之间的函数关系式.
任务2	结合素材1，2，小梅不改变发球的方向，射门路线的形状和最大高度保持不变此时足球能否进入球门?若不能进入，他应该带球向正后方至少移动多少米射门才能让足球进入球门
任务3	结合以上素材，小梅站在A处，只改变发球方向，射门路线的形状和最大高度保持不变，请探求此时足球能否越过拦网，在点E处进入球门
上述任务1、任务2、任务3中球落在门柱边线视同足球进入球门

答案解析收藏纠错 + 选题

5. (2023九上·温州期中) 根据以下素材，探索完成任务

确定文具套装售价
素材1	某书店销售一款文具套装，当每套文具售价为30元时，月销售量为200套，经市场调查表明，每套文具售价每降价1元，则月销售量增加20套．设每套文具的售价为x元(x为正整数)，月销售量为y套.
素材2	该文具套装的成本是10元/套．
素材3	为促进公益，在售价不低于进价且每套文具获利不高于95%的前提下，该书店决定，每月捐赠400元给慈善机构.
问题解决
任务1	分析变量关系	求y关于x的函数表达式.
任务2	计算月利润	当售价为多少时，月利润W获得最大?最大利润是多少?
任务3	确定合理售价	为了保证捐款后月利润不低于3040元，文具套装的售价可以取哪些数值.

答案解析收藏纠错 + 选题

6. (2023九上·金华月考) 根据以下素材，探究完成任务


素材1	图1是一个瓷碗，图2是其截面图，碗体DEC呈抛物线状(碗体厚度不计)，碗高GF=7cm，碗底宽AB=3cm，当瓷碗中装满面汤时，液面宽CD= 12cm，此时面汤最大深度EG= 6cm，
素材2	如图3，把瓷碗绕点B缓缓倾斜倒出部分面汤，当点A离MN距离为1.8cm时停止.
问题解决
任务1	确定碗体形状	在图2中建立合适的直角坐标系，求抛物线的函数表达式。
任务2	拟定设计方案1	根据图2位置，把碗中面汤喝掉一部分，当碗中液面高度(离桌面MN距离)为5cm时，求此时碗中液面宽度。
任务3	拟定设计方案2	如图3，当碗停止倾斜时，求此时碗中液面宽度CH。

答案解析收藏纠错 + 选题

7. (2024·镇海区月考) 根据以下素材，探索完成任务．

如何确定木板分配方案？
素材1	我校开展爱心义卖活动，小艺和同学们打算推销自己的手工制品．他们以每块15元的价格买了100张长方形木板，每块木板长和宽分别为80cm，40cm.
素材2	现将部分木板按图1虚线裁剪，剪去四个边长相同的小正方形（阴影）．把剩余五个矩形拼制成无盖长方体收纳盒，使其底面长与宽之比为3：1．其余木板按图2虚线裁剪出两块木板（阴影是余料），给部分盒子配上盖子．
素材3	义卖时的售价如标签所示：
问题解决
任务1	计算盒子高度	求出长方体收纳盒的高度．
任务2	确定分配方案1	若制成的有盖收纳盒个数大于无盖收纳盒，但不到无盖收纳盒个数的2倍，木板该如何分配？请给出分配方案．
任务3	确定分配方案2	为了提高利润，小艺打算把图2裁剪下来的余料（阴影部分）利用起来，一张矩形余料可以制成一把小木剑，并以5元/个的价格销售．请确定木板分配方案，使销售后获得最大利润．

答案解析收藏纠错 + 选题

8. (2023·嘉兴) 根据以下素材，探究完成任务．

如何把实心球掷得更远？
素材1
小林在练习投掷实心球，其示意图如图，第一次练习时，球从点A处被抛出，其路线是抛物线．点A距离地面 $\text{[math]}$ ，当球到 $\text{[math]}$ 的水平距离为 $\text{[math]}$ 时，达到最大高度为 $\text{[math]}$ ．
素材2
根据体育老师建议，第二次练习时，小林在正前方 $\text{[math]}$ 处（如图）架起距离地面高为 $\text{[math]}$ 的横线．球从点A处被抛出，恰好越过横线，测得投掷距离 $\text{[math]}$ ．
问题解决
任务1
计算投掷距离	建立合适的直角坐标系，求素材1中的投掷距离 $\text{[math]}$ ．
任务2
探求高度变化	求素材2和素材1中球的最大高度的变化量
任务3
提出训练建议	为了把球掷得更远，请给小林提出一条合理的训练建议．

答案解析收藏纠错 + 选题

9. (2024九上·杭州月考) 根据以下素材，探索完成任务

如何设计拱桥上救生圈的悬挂方案?
素材1	图1是一座抛物线形拱桥，以抛物线两个水平最低点连线为x轴，抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系，如图2所示．某时测得水面宽 $\text{[math]}$ ，拱顶离水面最大距离为10m，抛物线拱形最高点与x轴的距离为5m．据调查，该河段水位在此基础上再涨1m达到最高．
素材2	为方便救助溺水者，拟在图1的桥拱上方栏杆处悬挂救生圈，如图3，救生圈悬挂点为了方便悬挂，救生圈悬挂点距离抛物线拱面上方1m，且相邻两救生圈悬挂点的水平间距为4m．为美观，放置后救生圈关于y轴成轴对称分布．（悬挂救生圈的柱子大小忽略不计）

任务1	确定桥拱形状	根据图2，求抛物线的函数表达式．
任务2	拟定设计方案	求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
任务3	探究救生绳长度	当水位达到最高时，上游个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数）

问题解决

（1）任务1 确定桥拱形状
根据图2，求抛物线的函数表达式．
（2）任务2 拟定设计方案
求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
（3）任务3 探究救生绳长度
当水位达到最高时，上游个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数）

答案解析收藏纠错 + 选题

10. 根据以下素材，探索完成任务.

杨梅季将至，梅企与某快递公司合作寄送杨梅.

素材1

某快递公司规定：(1)从当地寄送杨梅到 $\text{[math]}$ 市按重量收费：当杨梅重量不超过10千克时，需要寄送费32元；当重量超过10千克时，超过部分另收 $\text{[math]}$ 元/千克.

(2)寄送杨梅重量均为整数千克.

素材2

（1）【分析变量关系】根据以上信息，请确定 $\text{[math]}$ 的值，并求出杨梅重量超过10千克时寄送费用 $\text{[math]}$ (元)关于杨梅重量 $\text{[math]}$ (千克)之间的函数关系式.
（2）【计算最省费用】若杨梅重量达到25千克，请求出最省的寄送费用.
（3）【探索最大重量】小聪想在当地梅企购买一批价格为50元/千克的杨梅并全部寄送给在 $\text{[math]}$ 市的朋友们，若小聪能用来支配的钱有5000元，他最多可以购买多少千克的杨梅?
并写出一种寄送方式.

答案解析收藏纠错 + 选题

11. (2023·深圳模拟) 【项目式学习】
项目主题：守护生命，“数”说安全．
项目背景：随着社会的发展，安全问题变得日益重要．某校为了提高学生的安全意识，开展以“守护生命，'数'说安全”为主题的项目式学习活动．创新小组通过考察测量、模拟探究和成果迁移等环节，开展地下弯道对通行车辆长度的限制研究．
1. （1）任务一：考察测量
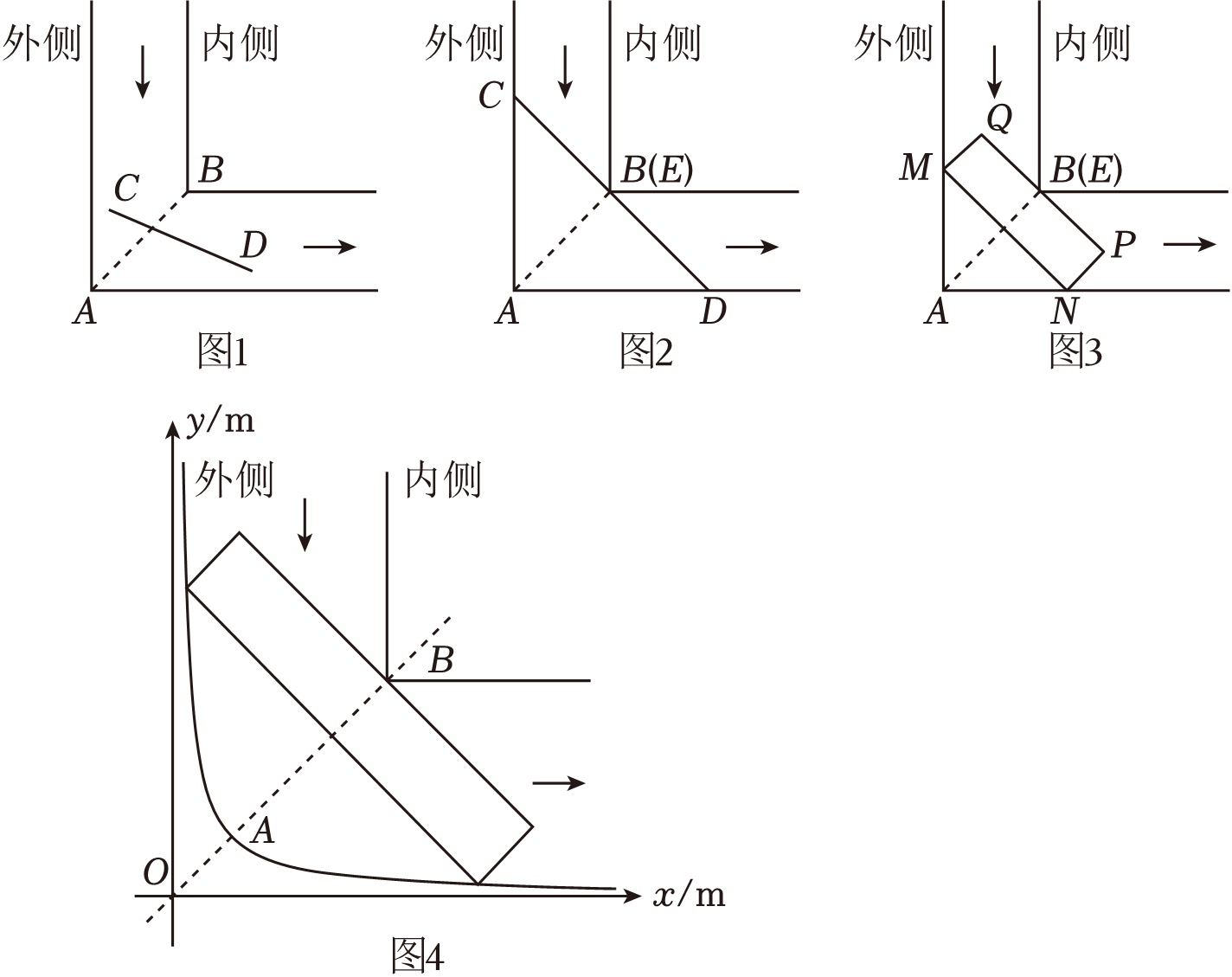
  如图1，创新小组所选取弯道的内、外侧均为直角，道路宽均为4m，则AB＝m；
2. （2）任务二：模拟探究
  如果汽车在行驶中与弯道内、外侧均无接触，则可安全通过．
  创新小组用线段模拟汽车通过宽度相同的直角弯道，探究发现：
  ①当CD＜2AB时（如图1），线段CD能通过直角弯道；
  ②当CD＝2AB时，必然存在线段CD的中点E与点B重合的情况，线段CD恰好不能通过直角弯道（如图2）．此时，∠ADC的度数是；③当CD＞2AB时，线段CD不能通过直角弯道．
3. （3）如图3，创新小组用矩形PQMN模拟汽车通过宽均为4m的直角弯道，发现当PQ的中点E与点B重合，且PQ⊥AB时，矩形PQMN恰好不能通过该弯道．若PQ＝am，PN＝2m，且矩形PQMN能通过该直角弯道，求a的最大整数值．
4. （4）任务三：成果迁移
  如图4，某弯道外侧形状可近似看成反比例函数y＝ $\text{[math]}$ （x＞0）的图象，其对称轴交图象于点A．弯道内侧的顶点B在射线OA上，两边分别与x轴，y轴平行，OA＝2m，AB＝4 $\text{[math]}$ m．创新小组探究发现通过该弯道的原理与通过直角弯道类似．有一辆长为bm，宽为2m的汽车需要安全通过该弯道，则b的最大整数值为．（参考数据： $\text{[math]}$ ≈1.4， $\text{[math]}$ ≈1.7， $\text{[math]}$ ≈2.2， $\text{[math]}$ ≈2.6）
答案解析收藏纠错 + 选题
12. (2024·深圳模拟) 【项目化学习】
项目主题：从函数角度重新认识“阻力对物体运动的影响”．
项目内容：数学兴趣小组对一个静止的小球从斜坡滚下后，在水平木板上运动的速度、距离与时间的关系进行了深入探究，兴趣小组先设计方案，再进行测量，然后根据所测量的数据进行分析，并进一步应用。
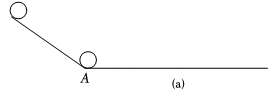
实验过程：如图（a）所示，一个黑球从斜坡顶端由静止滚下沿水平木板直线运动，从黑球运动到点A处开始，用频闪照相机、测速仪测量并记录黑球在木板上的运动时间x（单位：s）、运动速度v（单位：cm/s）、滑行距离y（单位：cm）的数据．
任务一：数据收集
记录的数据如下：
运动时间x/s
0
2
4
6
8
10
…
运动速度v/（cm/s）
10
9
8
7
6
5
…
滑行距离y/cm
0
19
36
51
64
75
…
根据表格中的数值分别在图（b）、图（c）中作出v与x的函数图象、y与x的函数图象：
1. （1）请在图（b）中画出v与x的函数图象：
2. （2）【任务二：观察分析】数学兴趣小组通过观察所作的函数图象，并结合已学习过的函数知识，发现图（b）中v与x的函数关系为一次函数关系，图（c）中y与x的函数关系为二次函数关系．请你结合表格数据，分别求出v与x的函数关系式和y与x的函数关系式：（不要求写出自变量的取值范围）
3. （3）【任务三：问题解决】当黑球在水平木板停下来时，求此时黑球的滑行距离：
4. （4）若黑球到达木板点A处的同时，在点A的前方 $\text{[math]}$ 处有一辆电动小车，以2cm/s的速度匀速向右直线运动，若黑球不能撞上小车，则n的取值范围应为．
答案解析收藏纠错 + 选题
13. (2022·江北模拟) 项目化学习：车轮的形状．
【问题提出】车轮为什么要做成圆形，这里面有什么数学原理?
1. （1）
  【合作探究】
  
  探究 $\text{[math]}$ 组：如图1，圆形车轮半径为 $\text{[math]}$ ，其车轮轴心 $\text{[math]}$ 到地面的距离始终为 $\text{[math]}$ ．
  探究 $\text{[math]}$ 组：如图2，正方形车轮的轴心为 $\text{[math]}$ ，若正方形的边长为 $\text{[math]}$ ，求车轮轴心 $\text{[math]}$ 最高点与最低点的高度差．
  探究 $\text{[math]}$ 组：如图3，有一个破损的圆形车轮，半径为 $\text{[math]}$ ，破损部分是一个弓形，其所对圆心角为 $\text{[math]}$ ，其车轮轴心为 $\text{[math]}$ ，让车轮在地上无滑动地滚动一周，求点 $\text{[math]}$ 经过的路程．
  
  探究发现：车辆的平稳关键看车轮轴心是否稳定．
2. （2）
  【拓展延伸】如图4，分别以正三角形的三个顶点 $\text{[math]}$ 为圆心，以正三角形的边长为半径作 $\text{[math]}$ 圆弧，这个曲线图形叫做“莱洛三角形”．
  
  探究 $\text{[math]}$ 组：使 “莱洛三角形” 沿水平方向向右滚动，在滚动过程中，其每时每刻都有 “最高点”，“中心点” 也在不断移动位置，那么在 “莱洛三角形” 滚动一周的过程中，其“最高点”和“中心点”所形成的图案大致是．
  延伸发现：“莱洛三角形”在滚动时始终位于一组平行线之间，因此放在其上的物体也能够保持平衡，但其车轴中心 $\text{[math]}$ 并不稳定．
答案解析收藏纠错 + 选题

14. (2023九上·杭州期中) 完成项目化学习：《蔬菜大棚的设计》．

《蔬菜大棚的设计》
驱动问题	1、如何利用函数模型，刻画蔬菜大棚的棚面？ 2、如何安装排气装置，保证蔬菜大棚的通风性？ 3、如何设计大棚间距，保障蔬菜大棚的采光性？
项目背景	蔬菜大棚是一种具有出色的保温性能的框架覆膜结构，它出现使得人们可以吃到反季节蔬菜．如图，一般蔬菜大棚使用竹结构或者钢结构的骨架，这样就形成了一个温室空间．
数学建模	如图，某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成，其中AB＝3m，取BC中点O，过点O作线段BC的垂直平分线OE交抛物线AED于点E，BC所在直线为x轴，OE为y轴建立如图所示平面直角坐标系．抛物线AED的顶点E（0，4）
问题解决	如图，为了保证该蔬菜大棚的通风性，该大棚要安装两个正方形孔的排气装置LFGT，若FL＝NR＝0.75m，求两个正方形装置的间距GM的长．
问题解决	为了保证两个蔬菜大棚间的采光不受影响，如图，在某一时刻，此时大棚截面的阴影为CK，求CK的长．

答案解析收藏纠错 + 选题

15. (2023九上·浑源月考) 综合与实践
【项目学习】

配方法是数学中重要的一种思想方法，利用配方法可求一元二次方程的根，也可以求二次函数的顶点坐标等．所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．其实这种方法还经常被用到代数式的变形中，并结合非负数的意义解决某些问题．

例1：把代数式 $\text{[math]}$ 进行配方．

解：原式 $\text{[math]}$ ．

例2：求代数式 $\text{[math]}$ 的最大值．

解：原式 $\text{[math]}$ ．

$\text{[math]}$ ， $\text{[math]}$ ，

$\text{[math]}$ ， $\text{[math]}$ 的最大值为 $\text{[math]}$ ．

【问题解决】
1. （1）若 $\text{[math]}$ 满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
2. （2）若等腰 $\text{[math]}$ 的三边长 $\text{[math]}$ 均为整数，且满足 $\text{[math]}$ ，求 $\text{[math]}$ 的周长．
3. （3）如图，这是美国总统加菲尔德证明勾股定理的一个图形，其中 $\text{[math]}$ 是 $\text{[math]}$ 和 $\text{[math]}$ 的三边长，根据勾股定理可得 $\text{[math]}$ ，我们把关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 称为“勾系一元二次方程”．已知实数 $\text{[math]}$ 满足等式 $\text{[math]}$ ，且 $\text{[math]}$ 的最小值是“勾系一元二次方程” $\text{[math]}$ 的一个根．四边形 $\text{[math]}$ 的周长为 $\text{[math]}$ ，试求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题

16. (2023九上·龙湾期中) 根据素材回答问题：

素材1	如图1，空地上有两条互相垂直的小路OP，OQ，中间有一正方形ABCD水池，已知水池的边长为4 米，AB//OQ，AD//OP，且AB与OQ的距离为10 米，AD与OP的距离为8 米．
素材2	现利用两条小路，再购置30 米长的栅栏(图中的细实线）在空地上围出一个花圃，要求围起来的栅栏与小路相互平行（或垂直），靠小路和水池的都不需要栅栏，接口损耗忽略不计．
	任务1	任务2
	小明同学按如图2的设计，若EF=16米，求出花圃的面积（不包含水池的面积）．	若按如图3、如图4设计方案，通过计算说明哪种方案的最大面积更大．
项目反思	如果栅栏不一定与墙面垂直（或平行），你还能设计出比以上方案面积更大的花圃吗？某学习小组在探究的过程中，设计了方案如图5，你认为图5的最大面积与以上方案比较，哪个更大，请通过计算说明．

答案解析收藏纠错 + 选题

17. (2023九上·义乌月考) 请根据素材，完成任务.

素材一	如图，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，若保证 $\text{[math]}$ 始终为直角，则点A、B、C在以AB为直径的圆上.
素材二	如图，在Rt△ABC中， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，取AB的中点 $\text{[math]}$ ，连接OC，根据“直角三角形斜边上的中线等于斜边的一半”可知 $\text{[math]}$ ，可得OC≥CD.
素材三	如图，矩形ABCD是某实验室侧截面示意图，现需要在室内安装一块长1米的遮光板EF，且EF//AB，点 $\text{[math]}$ 到墙AB的距离为4米，到地面BC的距离为5米.点O为室内光源，OM、ON为光线， $\text{[math]}$ ，通过调节光源的位置，可以改变背光工作区的大小.若背光工作区BM+BN的和最大时，该实验室“可利用比”最高.
任务一	若素材一中的AB=4，求CD的最大值.
任务二	若素材二中的CD=6，求AB的最小值.
任务三	若任务二中的∠ACB=90°改成∠ACB=60°，其余条件不变，请直接写出AB的最小值.
任务四	若任务二中的∠ACB=90°，CD=6改成∠ACB=α，CD=m，请直接出AB的最小值.
任务五	当素材三中的实验室“可利用比”最高，求此时BM+BN的值

答案解析收藏纠错 + 选题

18. (2023九上·瑞安月考) 阅读素材，完成任务．

测试机器人行走路径
素材一	图1是某校科技兴趣小组设计的一个可以帮助餐厅上菜的机器人，该机器人能根据指令要求进行旋转和行走．如图为机器人所走的路径．机器人从起点出发，连续执行如下指令：机器人先向前直行 $\text{[math]}$ （表示第 $\text{[math]}$ 次行走的路程），再逆时针旋转 $\text{[math]}$ ，直到第一次回到起点后停止．记机器人共行走的路程为 $\text{[math]}$ ，所走路径形成的封闭图形的面积为S ．
素材二	如图2，当每次直行路程均为1（即 $\text{[math]}$ ）， $\text{[math]}$ 时，机器人的运动路径为 $\text{[math]}$ ，机器人共走的路程 $\text{[math]}$ ，由图2图3易得所走路径形成的封闭图形的面积为 $\text{[math]}$ ．
素材三	如图4，若 $\text{[math]}$ ，机器人执行六次指令后回到起点处停止．
解决问题
任务	固定变量	探索变量	探索内容
任务一	直行路程 $\text{[math]}$ $\text{[math]}$	旋转角度 $\text{[math]}$ 与路程 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
			$\text{[math]}$
任务二	旋转角度 $\text{[math]}$	直行路程 $\text{[math]}$	若 $\text{[math]}$ ，求 $\text{[math]}$ 与 $\text{[math]}$ 的值．
任务三	旋转角度 $\text{[math]}$ ，路程 $\text{[math]}$	路径形成的封闭图形面积S ．	若 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并求出当S最大时 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题

19. (2024·瑞昌模拟) 根据以下材料，探索完成任务：

智能浇灌系统使用方案
材料				如图1是一款智能浇灌系统，水管OP垂直于地面并可以随意调节高度（OP最大高度不超过2.4m），浇灌花木时，喷头P处会向四周喷射水流形成固定形状的抛物线，水流落地点M与点O的距离即为最大浇灌距离，各方向水流落地点形成一个以点O为圆心，OM为半径的圆形浇灌区域．当喷头P位于地面与点O重合时，某一方向的水流上边缘形成了如图2的抛物线，经测量， $\text{[math]}$ ，水流最高时距离地面0.1m．如图3，农科院将该智能浇灌系统应用于一个长8m，宽6m的矩形试验田中，水管放置在矩形中心O处．
问题解决
任务1		确定水流形状	在图2中建立合适的平面直角坐标系，求抛物线的函数表达式．
任务2		探究浇灌最大区域	当调节水管OP的高度时，浇灌的圆形区域面积会发生变化，请你求出最大浇灌圆形区域面积．（结果保留 $\text{[math]}$ ）
任务3		解决具体问题	若要保证浇灌区域能完全覆盖矩形试验田，则水管OP至少需要调节到什么高度？

答案解析收藏纠错 + 选题

20. (2024九下·温州开学考) 根据下列素材，完成相应任务

仓储品装容的优化设计
素材1	如图1是某个仓库，图2是其横截面的示意图，已知墙体OA=2.6米，BC=5米，水平距离OC=12米，其顶部的轮廓为抛物线的一部分，建立如图所示的平面直角坐标系后它可以近似地用函数 y= $\text{[math]}$ x²+bx+c表示
素材2	图3是棱长为1m的立方体仓储品，将四件一样的仓储品如图4所示叠放在MN处，MN=1m.当叉车要取货物时，需要将其向上抬升10cm，沿水平方向移动1米后取出。
素材3	如图5，为保证能够用叉车安全顺利地搬运和放置仓储品进出仓库，需设计三条宽度为2米的过道OE，HC，FG，以及在过道之间设计两块宽度不少于2米的仓储区域EF，GH. 要求： ①靠近过道的仓储品需从就近过道搬运，其余可从左或右搬运。 ②尽可能多的装容仓储品.
问题解决
任务1	确定顶部形状	求仓库离地的最大距离.
任务2	确定摆放高度	当OM=2.4米时，试分别判断叉车能否从左边或右边取出?请说明理由。
任务3	设计最优方案	已知该仓库的长为50米，请你根据素材和要求设计：仓储区EF= ▲米， GH= ▲米，仓库最大仓储品容量为 ▲件.

答案解析收藏纠错 + 选题

试卷信息