
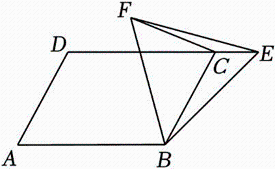
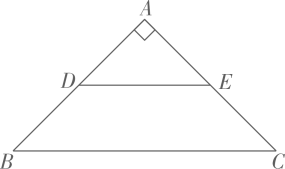
①点D是定点;
②AC•BC的最大值为50;
③D为△ABE的外心;
④CA+CB的最大值为 .
其中正确的有( )


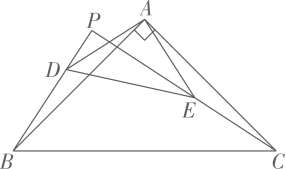
①;②
存在最大值为
;③
存在最小值为
;④点P运动的路径长为
. 其中,正确的是( )







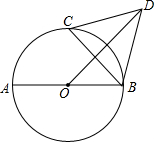
①当时
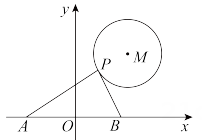
, 求出此时r的值;
②对于取定的r值,若存在两个α使 , 直接写出r的范围.
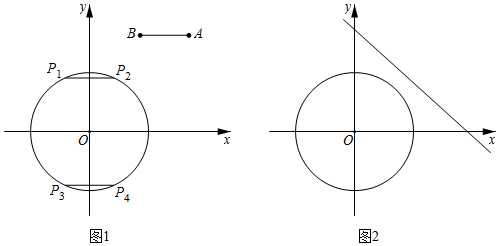
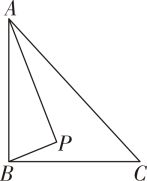
 ①在点O视角下,则线段
①在点O视角下,则线段 的“宽度
”为;
②若 半径为1.5,在点A视角下,
的“宽度
”为;
若随着点C位置的变化,使得在所有点K的视角下,线段 的“宽度”均满足
,直接写出m的取值范围.