新定义型—浙江省八（上）数学期末复习

更新时间：2025-01-02 浏览次数：14 类型：复习试卷

一、选择题

1. (2024八上·舟山期末) 定义运算：对于实数 $\text{[math]}$ ， $\text{[math]}$ ．例如 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，对于某个确定的 $\text{[math]}$ ，有且只有一个 $\text{[math]}$ 使等式成立，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八上·宁海期末) 高斯函数 $\text{[math]}$ ，也称为取整函数，即 $\text{[math]}$ 表示不超过 $\text{[math]}$ 的最大整数.例如： $\text{[math]}$ ， $\text{[math]}$ 则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③若 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是 $\text{[math]}$ ；④当 $\text{[math]}$ 时， $\text{[math]}$ 的值为0，1，2其中正确结论的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
3. (2024八上·鄞州期中) 对于任意实数p、q，定义一种运算：p@q＝p-q＋pq，例如2@3＝2-3＋2×3.请根据上述定义解决问题：若关于x的不等式组 $\text{[math]}$ 有3个整数解，则m的取值范围为是（）

A . -8≤m<-5 B . -8<m≤-5 C . -8≤m≤-5 D . -8<m<-5

答案解析收藏纠错 + 选题

二、填空题

4. (2024八上·上城期末) 定义：若一个三角形一边上的中线、高线与这条边有两个交点，这两个交点之间的距离称为这条边上的“中高距”．如图， $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 边上的中线， $\text{[math]}$ 为 $\text{[math]}$ 边上的高线，则 $\text{[math]}$ 的长称为 $\text{[math]}$ 边上的“中高距”．
1. （1）若 $\text{[math]}$ 边上的“中高距”为0，则 $\text{[math]}$ 的形状是三角形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 边上的“中高距”为．
答案解析收藏纠错 + 选题
5. (2024八上·濠江月考) 当三角形中一个内角β是另外一个内角a的 $\text{[math]}$ 时，我们称此三角形为“友好三角形”．如果一个“友好三角形”中有一个内角为 $\text{[math]}$ ，那么这个“友好三角形”的“友好角a”的度数为．

答案解析收藏纠错 + 选题
6. (2023八上·鄞州期末) 定义：对于实数a，符号 $\text{[math]}$ 表示不大于a的最大整数.例如： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .如果 $\text{[math]}$ ，则满足条件的所有正整数x的值是.

答案解析收藏纠错 + 选题
7. (2024八上·南湖月考) 定义：如果一个三角形的一条边是另一条边长度的两倍，则称这个三角形为倍长三角形．若等腰△ABC是倍长三角形，且一边长为6，则△ABC的底边长为．

答案解析收藏纠错 + 选题

三、解答题

8. (2023八上·西湖期末) 定义关于@的一种运算： $\text{[math]}$ ，如 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，且x为正整数，求x的值．
2. （2）若关于x的不等式 $\text{[math]}$ 的解和 $\text{[math]}$ 的解相同，求a的值．
答案解析收藏纠错 + 选题
9. (2024八上·滨江期末) 定义：一次函数 $\text{[math]}$ 和一次函数 $\text{[math]}$ 为“逆反函数”，如 $\text{[math]}$ 和 $\text{[math]}$ 为“逆反函数”．
1. （1）点 $\text{[math]}$ 在 $\text{[math]}$ 的“逆反函数”图象上，则 $\text{[math]}$ ；
2. （2） $\text{[math]}$ 图象上一点 $\text{[math]}$ 又是它的“逆反函数”图象上的点，求点B的坐标；
3. （3）若 $\text{[math]}$ 和它的“逆反函数”与y轴围成的三角形面积为3，求b的值．
答案解析收藏纠错 + 选题
10. (2024八上·杭州期中) 对于任意实数a，b，定义关于@的一种运算如下 $\text{[math]}$ ，例如 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）填空： $\text{[math]}$ _________； $\text{[math]}$ _________；
2. （2）若 $\text{[math]}$ ，求x的取值范围．
3. （3）若关于x的不等式 $\text{[math]}$ 恰有两个正整数解，求m的取值范围．
答案解析收藏纠错 + 选题
11. (2024八上·义乌期末) 两个顶角相等的等腰三角形，如果具有公共的顶角顶点，把它们的底角顶点连接起来形成一组可证得全等的三角形，我们把连接的那两条线段叫做“友好”线段．例如：如图1， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 中， $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，则可证得 $\text{[math]}$ ，此时线段 $\text{[math]}$ 和线段 $\text{[math]}$ 就是一对“友好”线段．
1. （1）如图2， $\text{[math]}$ 和 $\text{[math]}$ 都是等腰直角三角形，且 $\text{[math]}$ ．
  ①图中线段 $\text{[math]}$ 的“友好”线段是；
  ②连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）如图3， $\text{[math]}$ 是等腰直角三角形， $\text{[math]}$ 是 $\text{[math]}$ 外一点， $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
12. (2024八上·鄞州期末) 定义：若 $\text{[math]}$ 是 $\text{[math]}$ 的三边，且 $\text{[math]}$ ，则称 $\text{[math]}$ 为“方倍三角形”．
1. （1）若 $\text{[math]}$ 是“方倍三角形”，且斜边AB= $\text{[math]}$ ，则该三角形的面积为____．
2. （2）如图， $\text{[math]}$ 是“方倍三角形”，且 $\text{[math]}$ ，求证： $\text{[math]}$ 为等边三角形．
3. （3）如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上一点，将 $\text{[math]}$ 沿 $\text{[math]}$ 进行折叠，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 为“方倍三角形”，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
13. (2024八上·浙江期中) 定义：如果一条线段将一个三角形分成两个等腰三角形，我们把这条线段叫做这个三角形的“二分线”；如果两条线段将一个三角形分成三个等腰三角形，我们把这两条线段叫做这个三角形的“三分线”．
1. （1）三角形内角度数如图1所示，在图中画出“二分线”，并标出每个等腰三角形的顶角度数；
2. （2）图2是一个顶角为 $\text{[math]}$ 的等腰三角形，在图中画出“三分线”，并标出每个等腰三角形的顶角度数；
3. （3）在 $\text{[math]}$ 中，其最小的内角 $\text{[math]}$ ，过顶点B的一条线段是 $\text{[math]}$ 的“二分线”，请直接写出 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
14. (2024八上·瑞安期中) 我们新定义一类三角形：有两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形．例如，某三角形的三边长分别是2， $\text{[math]}$ ，因为 $\text{[math]}$ =2 $\text{[math]}$ ，所以这个三角形是奇异三角形
1. （1）若△ABC的三边长分别是3，4和 $\text{[math]}$ ，判断此三角形是否为奇异三角形，请说明理由．
2. （2）若Rt△ABC是奇异三角形，直角边分别为a，b，斜边为c，请探究a和b满足的数量关系式．
答案解析收藏纠错 + 选题
15. (2024八上·余姚期末) 如图，在平面直角坐标系中，点A（0，8），B（﹣4，0），C（4，0），给出如下定义：若P为△ABC内（不含边界）一点，且BP与△APC的一条边相等，则称点P为△ABC的和谐点．
1. （1）在P₁（﹣1，1），P₂（2，2），P₃（0，5）中，△ABC的和谐点是；
2. （2）若点P为△ABC的和谐点，且∠ABP＝45°，求点P的坐标；
3. （3）直线l为过点M（0，m）且与x轴平行的直线，若直线l上存在△ABC的二个和谐点，请直接写出m的取值范围．
答案解析收藏纠错 + 选题

四、实践探究题

16. (2024八上·长兴期中) 定义：把斜边重合，且直角顶点不重合的两个直角三角形叫做共边直角三角形
1. （1）概念理解：如图1，在△ABC中，∠C=90°，作出△ABC的共边直角三角形（画一个就行）；
2. （2）问题探究：如图2.△ABC和△DBC是共边直角三角形，E、F分别是AD、BC的中点，连接EF，求证：EF⊥AD.
3. （3）拓展延伸：如图3所示，△ABC和△ABD是共边直角三角形，BD=CD，求证：AD平分∠CAB.
答案解析收藏纠错 + 选题
17. (2023八上·宁波期末) 定义：若 $\text{[math]}$ 是 $\text{[math]}$ 的三边，且 $\text{[math]}$ ，则称 $\text{[math]}$ 为“方倍三角形”．
1. （1）若 $\text{[math]}$ 是“方倍三角形”，且斜边AB= $\text{[math]}$ ，则该三角形的面积为．
2. （2）如图， $\text{[math]}$ 是“方倍三角形”，且 $\text{[math]}$ ，求证： $\text{[math]}$ 为等边三角形．
3. （3）如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上一点，将 $\text{[math]}$ 沿 $\text{[math]}$ 进行折叠，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 为“方倍三角形”，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
18. (2024八上·东阳月考) 我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点．
1. （1）特例感知
  ①等腰直角三角形 ▲ 勾股高三角形（请填写“是”或者“不是”）；
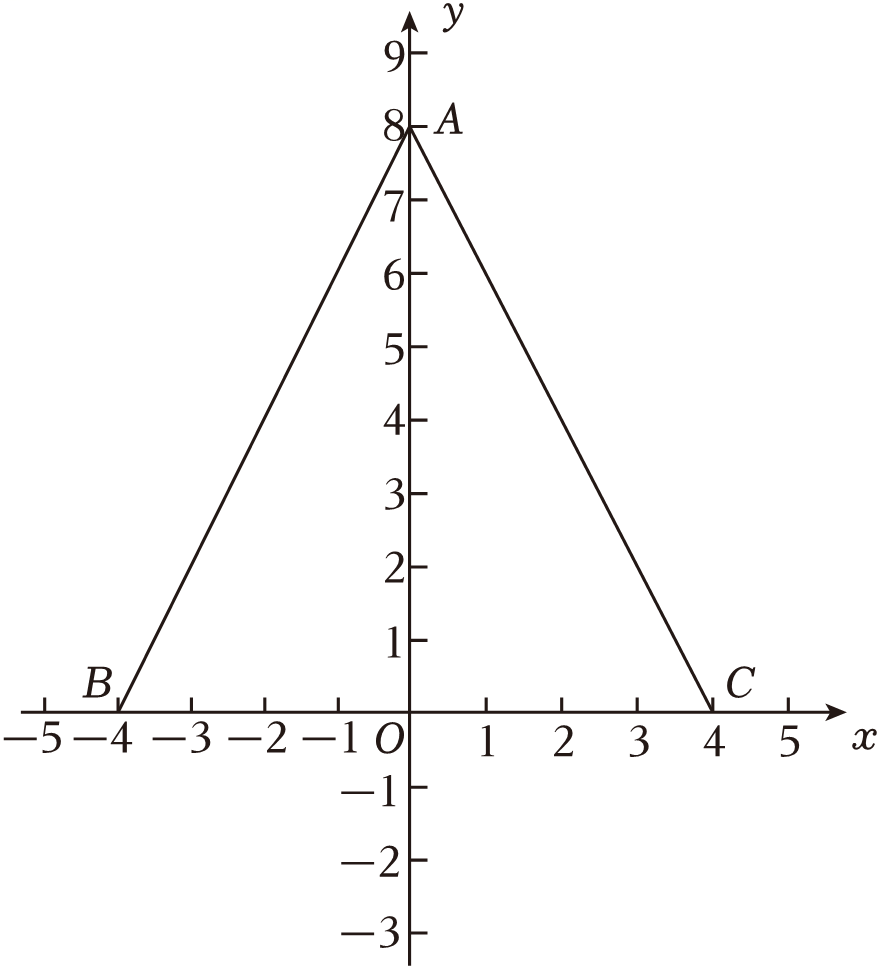
  ②如图1，已知 $\text{[math]}$ 为勾股高三角形，其中C为勾股顶点， $\text{[math]}$ 是 $\text{[math]}$ 边上的高．若 $\text{[math]}$ ，试求线段 $\text{[math]}$ 的长度．
2. （2）深入探究
  如图2，已知 $\text{[math]}$ 为勾股高三角形，其中C为勾股顶点且 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的高，试探究线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并给予证明；
3. （3）推广应用
  如图3，等腰 $\text{[math]}$ 为勾股高三角形，其中 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的高，过点D向 $\text{[math]}$ 边引平行线与 $\text{[math]}$ 边交于点E ．若 $\text{[math]}$ ，试求线段 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
19. (2024八上·浙江期中) 新定义：我们把两个面积相等但不全等的三角形叫做偏等积三角形.
1. （1）初步尝试
  如图1，在△ABC中，∠ACB＝90°，AC＝BC＝6，P为AC上一点，当AP的长为时，△ABP与△CBP为偏等积三角形.
2. （2）理解运用
  如图2，△ABD与△ACD为偏等积三角形，AB＝2，AC＝4，且线段AD的长度为正整数，过点C作CE∥AB，交AD的延长线于点E，求AE的长.
3. （3）综合应用
  如图3，已知△ABC和△ADE为两个等腰直角三角形，其中AC＝AB，AD＝AE，∠CAB＝∠DAE＝90°，F为CD的中点.请根据上述条件，回答以下问题：
  ①∠CAD+∠BAE的度数为 °；
  ②试探究线段AF与BE的数量关系，并写出解答过程.
答案解析收藏纠错 + 选题