题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

浙教版2019中考数学复习专题之三角形综合题

更新时间：2021-05-20 浏览次数：749 类型：二轮复习

一、解答题

1. 已知：如图1，过等腰直角三角形ABC的直角顶点A作直线AP，点B关于直线AP的对称点为E，连接BE，CE，其中CE交直线AP于点F．
1. （1）依题意补全图形；
2. （2）若∠PAB＝16°，求∠ACF的度数；
3. （3）如图2，若45°＜∠PAB＜90°，用等式表示线段AB，FE，FC之间的数量关系，并证明．
答案解析收藏纠错 + 选题
2. (2021七下·东莞期末) 如图1，P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动，点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动，在直角三角形ABC中，∠A＝90°，若AB＝16厘米，AC＝12厘米，BC＝20厘米，如果P、Q同时出发，用t（秒）表示移动时间，那么：
1. （1）如图1，若P在线段AB上运动，Q在线段CA上运动，试求出t为何值时，QA＝AP
2. （2）如图2，点Q在CA上运动，试求出t为何值时，三角形QAB的面积等于三角形ABC面积的 $\text{[math]}$ ；
3. （3）如图3，当P点到达C点时，P、Q两点都停止运动，试求当t为何值时，线段AQ的长度等于线段BP的长的 $\text{[math]}$
答案解析收藏纠错 + 选题
3. 已知：如图，∠MON＝90°，△ABC中，∠C＝90°，AC＝3cm，BC＝4cm，将△ABC的两个顶点A、B放在射线OM和ON上移动，作CD⊥ON于点D，记OA＝x（当点O与A重合时，x的值为0），CD＝y．
小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

下面是小明的探究过程，请补充完整．
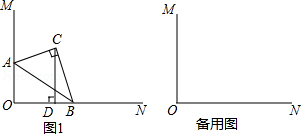
1. （1）通过取点、画图、计算、测量等方法，得到了x与y的几组值，如下表（补全表格）
  
  x/cm
  
  0
  
  1
  
  2
  
  3
  
  4
  
  4.5
  
  5
  
  y/cm
  
  2.4
  
  3.0
  
  3.5
  
  3.9
  
  4.0
  
  3.9
  
  （说明：补全表格时相关数值保留一位小数）
2. （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．
3. （3）结合画出的函数图象，解决问题；当x的值为时，线段OC长度取得最大值为cm．
答案解析收藏纠错 + 选题
4. △ABC中，AB＝AC＝a，∠EDF的顶点D是底边BC的中点，两边分别与AB、AC交于点F、E，研究BF和CE之间的数量关系．为此，可以用从特殊到一般的方法进行研究．
1. （1）研究特例．如图1，∠A＝90°，∠EDF＝90°，当E，F的位置变化时，BF+CE是否随之变化？证明你的结论；
2. （2）变式迁移．如图2，当∠A＝120°，a＝6，当∠EDF＝°时，（1）中的结论仍然成立，求出此时BF+CE的值；
3. （3）推广到一般．如图3，当∠BAC和∠EDF满足什么关系时，（1）中的结论仍然成立？若G是射线BA上的一点，且BG＝BF+CE，请直接写出∠BGC的度数．
答案解析收藏纠错 + 选题
5. 问题情境：如图1，在直角三角形ABC中，∠BAC＝90°，AD⊥BC于点D，可知：∠BAD＝∠C（不需要证明）；
1. （1）特例探究：如图2，∠MAN＝90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB＝AC，CF⊥AE于点F，BD⊥AE于点D．证明：△ABD≌△CAF；
2. （2）归纳证明：如图3，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB＝AC，∠1＝∠2＝∠BAC．求证：△ABE≌△CAF；
3. （3）拓展应用：如图4，在△ABC中，AB＝AC，AB＞BC．点D在边BC上，CD＝2BD，点E、F在线段AD上，∠1＝∠2＝∠BAC．若△ABC的面积为3，则△ACF与△BDE的面积之和为．
答案解析收藏纠错 + 选题
6. 如图，已知△ABC中，∠B＝90°，AB＝16cm，BC＝12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．
1. （1）出发2秒后，求△PBQ的面积；
2. （2）当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？
3. （3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．
答案解析收藏纠错 + 选题
7. 如图1所示，等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，直线MN经过点A，BD⊥MN于点D，CE⊥MN于点E．
1. （1）求证：∠ABD＝∠CAE；
2. （2）求证：DE＝BD+CE；
3. （3）当直线MN运动到如图2所示位置时，其余条件不变，直接写出线段DE、BD、CE之间的数量关系．
答案解析收藏纠错 + 选题
8.
1. （1）阅读理解：
  如图1，在△ABC中，若AB＝10，AC＝6，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE＝AD，连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是；
2. （2）问题解决：如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．
答案解析收藏纠错 + 选题
9. 如图，点N是△ABC的边BC延长线上的一点，∠ACN＝2∠BAC，过点A作AC的垂线交CN于点P．
1. （1）若∠APC＝30°，求证：AB＝AP；
2. （2）若AP＝4，BP＝8，求AC的长；
3. （3）若点P在BC的延长线上运动，∠APB的平分线交AB于点M．你认为∠AMP的大小是否发生变化？若变化，请说明理由；若不变化，求出∠AMP的大小．
答案解析收藏纠错 + 选题
10. 如图所示，直线AB交x轴于点A（a，0）交y轴于点B （0，b），且a、b满足 $\text{[math]}$ ＝0，P为线段AB上的一点．
1. （1）如图1，若AB＝6 $\text{[math]}$ ，当△OAP为AP＝AO的等腰三角形时，求BP的长．
2. （2）如图2，若P为AB的中点，点M、N分别是OA、OB边上的动点，点M从顶点A、点N从顶点O同时出发，且它们的速度都为1cm/s，则在M、N运动的过程中，S_{四边形PNOM}的值是否会发生改变？如发生改变，求出其面积的变化范围；若不改变，求该面积的值．
3. （3）如图3，若P为线段AB上异于A、B的任意一点，过B点作BD⊥OP，交OP、OA分别于F、D两点，E为OA上一点，且∠PEA＝∠BDO，试判断线段OD与AE的数量关系，并说明理由．
答案解析收藏纠错 + 选题
11. 将一个直角三角形纸板ABC放置在锐角△PMN上，使该直角三角形纸板的两条直角边AB，AC分别经过点M，N．
1. （1）【发现】
  ①如图1，若点A在△PMN内，当∠P＝30°时，则∠PMN+∠PNM＝°，∠AMN+∠ANM＝°，∠PMA+∠PNA＝°．
  
  ②如图2，若点A在△PMN内，当∠P＝50°时，∠PMA+∠PNA＝°．
2. （2）【探究】
  若点A在△PMN内，请你判断∠PMA，∠PNA和∠P之间满足怎样的数量关系，并写出理由．
3. （3）【应用】
  如图3，点A在△PMN内，过点P作直线EF∥AB，若∠PNA＝16°，则∠NPE＝．
答案解析收藏纠错 + 选题
12. 如图，在平面直角坐标系中，A、B两点的坐标分别为（﹣2，2）、（1，8）
1. （1）求三角形ABO的面积；
2. （2）若点M（﹣4，n），且三角形MAB的面积为10，求M点的坐标；
3. （3）如图，把直线AB以每秒1个单位的速度向右平移，问经过多少秒后，该直线与y轴交于点（0，﹣1）？
答案解析收藏纠错 + 选题
13. 已知△ABC为等腰三角形，AB＝AC，点D为直线BC上一动点（点D不与点B、点C重合）．以AD为边作△ADE，且AD＝AE，连接CE，∠BAC＝∠DAE．
1. （1）如图1，当点D在边BC上时，试说明：①△ABD≌△ACE；②BC＝DC+CE；
2. （2）如图2，当点D在边BC的延长线上时，其他条件不变，探究线段BC、DC、CE之间存在的数量关系，并说明理由．
答案解析收藏纠错 + 选题
14. 如图，O在等边△ABC内，∠AOB＝100°，∠BOC＝x，将△BOC绕点C顺时针旋转60°，得△ADC，连接OD．
1. （1） △COD的形状是；
2. （2）当x＝150°时，求△AOD的形状；此时若OB＝3，OC＝5，求OA的长；
3. （3）当x为多少度时，△AOD为等腰三角形．
答案解析收藏纠错 + 选题
15. 如图，直线AB交x轴于点A（3，0），交y轴于点B（0，2）
1. （1）求三角形AOB的面积；
2. （2）在x轴负半轴上找一点Q，使得S_△QOB＝S_△AOB ，求Q点坐标．
3. （3）在y轴上任一点P（0，m），请用含m的式子表示三角形APB的面积．
答案解析收藏纠错 + 选题
16. 已知AD是△ABC的外角平分线．
1. （1）如图（1），当AB＝AC时，求证：AD∥BC；
2. （2）如图（2），当AB＜AC时，BC的垂直平分线交AD于点P，PM⊥BA，交BA的延长线于点M，求证：AC＝2AM+AB；
3. （3）在（2）的条件下，如图（3）连接PC，若∠ACP＝30°，PM＝2AM，AC＝ $\text{[math]}$ PC，AM＝5，求AB的长．
答案解析收藏纠错 + 选题
17. 已知等腰△ABC中，AB＝AC，点D在直线AB上，DE∥BC，交直线AC于点E，且BD＝BC，CH⊥AB，垂足为H．
1. （1）当点D在线段AB上时，如图①，求证DH＝BH+DE；
  （提示：在DH上截取HM＝BH，连接CM，CD．）
2. （2）当点D在线段BA延长线上时，如图②；当点D在线段AB延长线上时，如图③，直接写出线段DH，BH，DE之间的数量关系，不需要证明；
3. （3）在（1）、（2）条件下，若CE＝7，BH＝3DE，则DH＝．
答案解析收藏纠错 + 选题
18. 如图，在平面直角坐标系xOy中，已知点A（3，0），点B（0，3 $\text{[math]}$ ），点O为原点．动点C、D分别在直线AB、OB上，将△BCD沿着CD折叠，得△B'CD．

（Ⅰ）如图1，若CD⊥AB，点B'恰好落在点A处，求此时点D的坐标；

（Ⅱ）如图2，若BD＝AC，点B'恰好落在y轴上，求此时点C的坐标；

（Ⅲ）若点C的横坐标为2，点B'落在x轴上，求点B'的坐标（直接写出结果即可）．

答案解析收藏纠错 + 选题
19. 已知等腰Rt△ABC中，∠C＝90°，AC＝5，点D为BC边上的一个定点，连接AD，点P为AC边上一个动点．
1. （1）如图1，若AD＝BP，CD＝2，求AP的长；
2. （2）如图2，∠CAD＝20°，点Q为AD上的一个动点，连接PQ、PD，当线段PQ与PD之和最小时，求∠PDQ的度数；
3. （3）在（2）问的条件下，将△ACD绕点D沿顺时针方向旋转得到△A′C′D，设旋转角为α（0°＜α＜180°），在旋转过程中，直线A'C'、直线A′D分别与AB所在的直线交于点E和F，是否存在这样的位置，使得△A'EF为等腰三角形？若存在，求出此时的旋转角α；若不存在，请说明理由．
答案解析收藏纠错 + 选题
20. 如图，已知△ABC中，AB＝AC＝10厘米，∠ABC＝∠ACB，BC＝8厘米，点D为AB的中点，如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动，设点P运动的时间为t．
1. （1）用含有t的代数式表示线段PC的长度；
2. （2）若点Q的运动速度与点P的运动速度相等，经过1秒后△BPD与△CQP是否全等，请说明理由；
3. （3）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
答案解析收藏纠错 + 选题
21. 如图1，点P、Q分别是边长为5cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为2cm/s．
1. （1）设运动时间为t秒，则BQ＝，BP＝．（用含t的代数式表示）并求出何时△PBQ是直角三角形；
2. （2）如图1，连接AQ、CP交于点M，在PQ运动的过程中，∠CMQ的度数有变化吗？若变化，请说明理由，若不变，直接写出它的度数．
3. （3）如图2，当点P、Q运动到射线AB、BC上时，直线AQ、CP交点为M，则∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数．
答案解析收藏纠错 + 选题
22. 动点型问题是数学学习中的常见问题，解决这类问题的关键是动中求静，运用分类讨论及数形结合的思想灵活运用有关数学知识解决问题．如图，在直角三角形ABC中，∠ACB＝90°，BC＝4cm，AC＝10cm，点D在射线CA上从点C出发向点A方向运动（点D不与点A重合），且点D运动的速度为2cm/s，设运动时间为x秒时，对应的△ABD的面积为ycm² ．
1. （1）填写下表：
  
  时间x秒
  
  …
  
  2
  
  4
  
  6
  
  …
  
  面积ycm²
  
  …
  
  12
  
  …
2. （2）在点D的运动过程中，出现△ABD为等腰三角形的次数有次，请用尺规作图，画出BD（保留作图痕迹，不写画法）；
3. （3）求当x为何值时，△ABD的面积是△ABC的面积的 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
23. 在△OAB中，OA＝OB，OA⊥OB．在△OCD中，OC＝OD，OC⊥OD．
1. （1）如图1，若A，O，D三点在同一条直线上，求证：S_△AOC＝S_△BOD；
2. （2）如图2，若A，O，D三点不在同一条直线上，△OAB和△OCD不重叠．则S_△AOC＝S_△BOD是否仍成立？若成立，请予以证明；若不成立，也请说明理由．
3. （3）若A，O，D三点不在同一条直线上，△OAB和△OCD有部分重叠，经过画图猜想，请直接写出 S_△AOC和S_△BOD的大小关系．
答案解析收藏纠错 + 选题
24. 已知：在△BCD中，∠BDC＝90°，BF平分∠DBC交CD于F，过点C作CE⊥BF交延长线于E，延长CE、BD交于点A．
1. （1）如图1，若BD＝CD．①求证：BF＝AC；②直接写出 $\text{[math]}$ 的值；
2. （2）如图2，过点D作DH⊥BC交BF于点G，垂足为H，过点G作GN∥BC交DC于点N，请判断DF与CN的数量关系，并说明理由．
答案解析收藏纠错 + 选题
25. 如图，在△ABC中，AB＝AC＝4cm，∠BAC＝100°，点D是BC上一个动点（不与B、C重合），连接AD，作∠ADE＝40°，DE交线段AC于E．
1. （1）求证：∠BAD＝∠EDC；
2. （2）当∠BAD等于多少时，△ABD≌△DCE？请说明理由；
3. （3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BAD的度数，若不可以，请说明理由．
答案解析收藏纠错 + 选题
26. 如图1所示，AE＝AF，AE⊥AF，E，F，B在同一直线上，AB＝AC，∠BAC＝90°．
1. （1）求证：∠EAB＝∠FAC
2. （2）判断△AEB与△AFC是否全等？若全等，请给出证明；若不全等，说明理由
3. （3）当EF＝FB时，如图2，求证：CE＝CB．
答案解析收藏纠错 + 选题
27. 如图，△ABC和△DBE均为等腰三角形，点A，D，E在同一直线上，连接CE．
1. （1）如图1，若∠BAC＝∠BCA＝∠BDE＝∠BED＝55°
  ①求证：AD＝CE；
  
  ②求∠AEC的度数．
2. （2）如图2，若∠ABC＝∠DBE＝120°，BM为△BDE中DE边上的高，CN为△ACE中AE边上的高，CN＝a，BM＝b试证明：AE＝ $\text{[math]}$ a+2 $\text{[math]}$ b．
答案解析收藏纠错 + 选题
28. 定义：对于平面直角坐标系xOy中的线段PQ和点M，在△MPQ中，当PQ边上的高为1时，称M为PQ的“等高点”，称此时MP+MQ为PQ的“等高距离”．
1. （1）若P（1，1），Q（4，1）．
  ①在点A（0，2），B（ $\text{[math]}$ ，3），C（1，0）中，PQ的“等高点”是（填字母）；
  
  ②若点M为PQ的“等高点”，求PQ的“等高距离”的最小值及此时点M的坐标．
2. （2）若P（0，0），PQ＝2，当PQ的“等高点”在y轴正半轴上且“等高距离”最小时，试求此时点Q的坐标．
答案解析收藏纠错 + 选题
29. 如图1，Rt△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿BC向点C以2cm/s的速度移动．如果P，Q同时分别从A，B点出发，设出发时间为ts（t＞0）．
1. （1）当t为何值时，△PBQ的面积是8cm²？
2. （2）当t为何值时，点P和点Q间的距离是6cm？
3. （3）如图2，若点P，点Q同时从B点出发，点P沿折线BA﹣AC移动，点Q沿折线BC﹣CA移动，其余条件均不变，求当P，Q在D点相遇时，点D与点B的距离．
答案解析收藏纠错 + 选题
30. 已知△ABC，AB＝AC，D为直线BC上一点，E为直线AC上一点，AD＝AE，设∠BAD＝α，∠CDE＝β．
1. （1）如图，若点D在线段BC上，点E在线段AC上．
  
  ①如果∠ABC＝60°，∠ADE＝70°，那么α＝°，β＝°．
  
  ②求α，β之间的关系式．
2. （2）是否存在不同于以上②中的α，β之间的关系式？若存在，求出这个关系式（求出一个即可）；若不存在，说明理由．
答案解析收藏纠错 + 选题
31. 如图，在等腰直角三角形ABC中，∠BAC＝90°，AC＝8 $\text{[math]}$ cm，AD⊥BC于点D．点P从点A出发，沿A→C方向以 $\text{[math]}$ cm/s的速度运动到点C停止．在运动过程中，过点P作PQ∥AB交BC于点Q，以线段PQ为边作等腰直角三角形PQM，且∠PQM＝90°（点M，C位于PQ异侧）．设点P的运动时间为x（s），△PQM与△ADC重叠部分的面积为y（cm²）
1. （1）当点M落在AB上时，求x的值；
2. （2）当点M落在AD上时，PM与CD之间的数量关系是，此时x的值是；
3. （3）求y关于x的函数解析式，并写出自变量x的取值范围．
答案解析收藏纠错 + 选题
32. (2019九上·湖州月考) 两个直角边为6的全等的等腰Rt△AOB和Rt△CED中，按图1所示的位置放置，A与C重合，O与E重合．
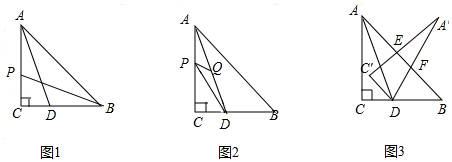
（Ⅰ）求图1中，A，B，D三点的坐标；

（Ⅱ）Rt△AOB固定不动，Rt△CED沿x轴以每秒2个单位长的速度向右运动，当D点运动到与B点重合时停止，设运动x秒后Rt△AOB和Rt△CED的重叠部分面积为y，求y与x之间的函数关系式；

（Ⅲ）当Rt△CED以（Ⅱ）中的速度和方向运动，运动时间x＝4秒时Rt△CED运动到如图2所示的位置，求点G的坐标．

答案解析收藏纠错 + 选题
33. 在△ABC中，∠ACB＝90°，CD为AB边上的高线，DE⊥AC于点E．
1. （1）若AD＝BC，求证：DE＝DB；
2. （2）若G是DE的中点，延长AG交BC于F．求证：F是BC的中点；
3. （3）在（2）的条件下，延长CG交AB于H，使AH＝BH，当AC＝4时，求DE的长．
答案解析收藏纠错 + 选题
34. 阅读材料：

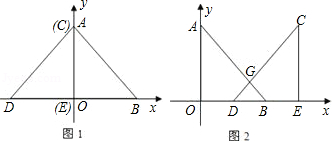
我们曾经解决过如下问题：“如图1，点M，N分别在直线AB同侧，如何在直线AB上找到一个点P，使得PM+PN最小？”

我们可以经过如下步骤解决这个问题：

①画草图（或目标图）分析思路：在直线AB上任取一点P′，连接P′M，P′N，根据题目需要，作点M关于直线AB的对称点M′，将P′M+P′N转化为P′M′+P′N′，“化曲为直”寻找P′M′+P′N的最小值；

②设计画图步骤；

③回答结论并验证．

解决下列两个问题：
1. （1）如图2，在△ABC中，AB＝3，AC＝4，BC＝5，EF垂直且平分BC，点P在直线EF上，直接写出PA+PB的最小值，回答PA+PB取最小值时点P的位置并在图中标出来；解：PA+PB的最小值为，PA+PB取最小值时点P的位置是；
2. （2）如图3，点M，N分别在直线AB两侧，在直线AB上找一点P，使得∠MPB＝∠NPB．要求画图，并简要叙述确定点P位置的步骤．（无需尺规作图，保留画图痕迹，无需证明）
  解：确定点P位置的简要步骤：．
答案解析收藏纠错 + 选题
35. 已知：如图，在△ABC中，AC＝AB＝10，BC＝16，动点P从A点出发，沿线段AC运动，速度为1个单位/s，时间为t秒，P点关于BC的对称点为Q．
1. （1）当t＝2时，则CN的长为；
2. （2）连AQ交线段BC于M，若AM＝2MQ，求t的值；
3. （3）若∠BAQ＝3∠CAQ时，求t的值．
答案解析收藏纠错 + 选题
36. (2020八上·罗庄期末) 如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．
1. （1）如图1，若∠CAB＝∠CBA＝∠CDE＝∠CED＝50°．
  ①求证：AD＝BE；
  
  ②求∠AEB的度数．
2. （2）如图2，若∠ACB＝∠DCE＝90°，CF为△DCE中DE边上的高，试猜想AE，CF，BE之间的关系，并证明你的结论．
答案解析收藏纠错 + 选题
37. 在等边△ABC中，E为BC边上一点，G为BC延长线上一点，过点E作∠AEM＝60°，交∠ACG的平分线于点M．
1. （1）如图（1），当点E在BC边的中点位置时，通过测量AE，EM的长度，猜想AE与EM满足的数量关系是；
2. （2）如图（2），小晏通过观察、实验，提出猜想：当点E在BC边的任意位置时，始终有AE＝EM．小晏把这个猜想与同学进行交流，通过讨论，形成了证明该猜想的几种想法：
  想法1：在BA上取一点H使AH＝CE，连接EH，要证AE＝EM，只需证△AHE≌△ECM．
  
  想法2：找点A关于直线BC的对称点F，连接AF，CF，EF．（易证∠BCF+∠BCA+ACM＝180°，∴M，C，F三点在同一直线上）要证AE＝EM，只需证△MEF为等腰三角形．
  
  想法3：将线段BE绕点B顺时针旋转60°，得到线段BF，连接CF，EF，要证AE＝EM，只需证四边形MCFE为平行四边形．
  
  请你参考上面的想法，帮助小晏证明AE＝EM．（一种方法即可）
答案解析收藏纠错 + 选题
38. 如图，A（0，4）是直角坐标系y轴上一点，动点P从原点O出发，沿x轴正半轴运动，速度为每秒1个单位长度，以P为直角顶点在第一象限内作等腰Rt△APB．设P点的运动时间为t秒．
1. （1）若AB∥x轴，求t的值；
2. （2）当t＝3时，坐标平面内有一点M，使得以M、P、B为顶点的三角形和△ABP全等，请直接写出点M的坐标；
3. （3）设点A关于x轴的对称点为A'，连接A'B，
  在点P运动的过程中，∠OA'B的度数是否会发生变化，
  
  若不变，请求出∠OA'B的度数，若改变，请说明理由．
答案解析收藏纠错 + 选题
39. 实践探究，解决问题

如图1，△ABC中，AD为BC边上的中线，则S_△ABD＝S_△ACD ．
1. （1）在图2中，E、F分别为矩形ABCD的边AD、BC的中点，且AB＝4，AD＝8，则S_阴影＝；
2. （2）在图3中，E、F分别为平行四边形ABCD的边AD、BC的中点，则S_阴影和S_{平行四边形ABCD}之间满足的关系式为；
3. （3）在图4中，E、F分别为任意四边形ABCD的边AD、BC的中点，则S_阴影和S_{四边形ABCD}之间还满足（2）中的关系式吗？若满足，请予以证明，若不满足，说明理由．
  解决问题：
4. （4）在图5中，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，并且图中阴影部分的面积为20平方米，求图中四个小三角形的面积和（即S₁+S₂+S₃+S₄的值）．
答案解析收藏纠错 + 选题
40. 我们引入如下概念，
定义；到三角形的两条边的距离相等的点，叫做此三角形的准内心，举例：如图1，PE⊥BC，若PE＝PD则P为△ABC的准内心
1. （1）填空；根据准内心的概念，图1中的点P在∠BAC的上．
2. （2）应用；如图2，△ABC中，AC＝BC＝13，AB＝10，准内心P在AB上，求P到AC边的距离PD的长．
3. （3）探究；已知△ABC为直角三角形，AC＝BC＝6，∠C＝90°，准内心P在△ABC的边上，试探究PC的长．
答案解析收藏纠错 + 选题

试卷信息