 B .
B . 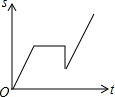 C .
C .  D .
D . 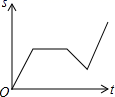

 B .
B . 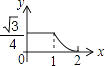 C .
C . 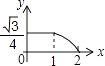 D .
D . 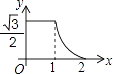


|
进价(元/个) |
售价(元/个) |
销量(个/日) |
|
|
A型 |
400 |
600 |
200 |
|
B型 |
800 |
1200 |
400 |
根据市场行情,该销售商对A型手写板降价销售,同时对B型手写板提高售价,此时发现A型手写板每降低5元就可多卖1个,B型手写板每提高5元就少卖1个.销售时保持每天销售总量不变,设其中A型手写板每天多销售x个,每天获得的总利润为y元.
例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2,并研究它在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
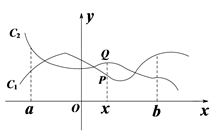
∵
a-2 +b=(
-
)2≥0 ∴ a-2
+b≥0
∴ a+b≥2 ∴
≥
其实,这个不等关系可以推广, ≥
… …
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时, ,则
有最小值.
再如:x为非负数时,x+x+ .
我们来研究函数:

|
x |
… |
-3 |
-2 |
-1 |
| | 1 | 2 | 3 | … |
| y | … | | 3 | | | 5 | | … |
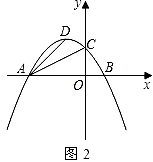
①求BC的长;
②若抛物线C2与直线l交于点E、F两点,若EF长大于BC的长。求出n的范围;
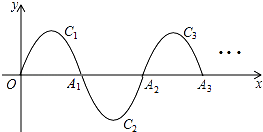
①若 ,试说明抛物线C1与抛物线C2的交点始终在定直线上;
②求y1+y2的最小值(用含k的代数式表示).
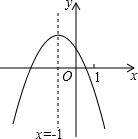
①求抛物线的解析式;
②若n>1,设点M(n,y1),N(n+1,y2)在抛物线上,比较y1 , y2的大小关系,并说明理由;
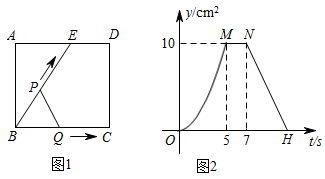
①若点Q为BC中点,求t的值;
②用t的代数式表示点Q的坐标和直线PQ的函数关系式;
③若M(2m,n-8),N(t3+2t2-2m,n)在直线PQ上,求n的取值范围.
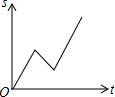
Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;
Ⅱ.社会工龄=参加本企业工作时年龄-18,
企业工龄=现年年龄-参加本企业工作时年龄.
Ⅲ.当年工作时间计入当年工龄
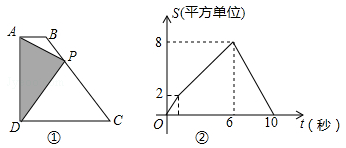
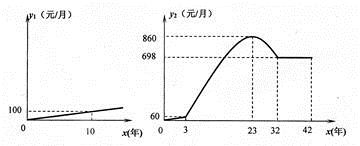
Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.
请解决以下问题
①当 、
时,求
的值;
②若 随
的增大而减小,求
的取值范围.
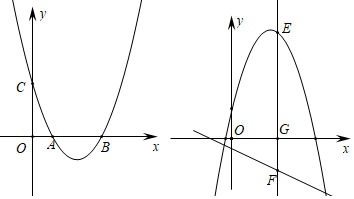
①当a=1时,直接写出抛物线y1和直线y2相应的函数表达式;
②如图,已知抛物线y1在3<x<4这一段位于直线y2的下方,在5<x<6这一段位于直线y2的上方,求a的取值范围;
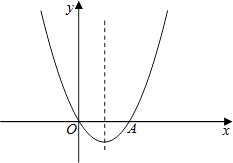
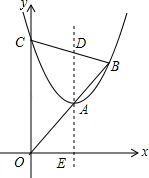
探究一:如图1,设△PAD的面积为S,令W=t•S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
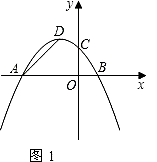
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.(参考资料:抛物线y=ax2+bx+c(a≠0)对称轴是直线x= )