题库组卷系统-专注K12在线组卷服务

在线咨询

当前：高中数学

当前位置：高中数学 /高考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

概率与统计（解答题）——大数据之五年（2018-2022）高...

更新时间：2022-07-31 浏览次数：164 类型：一轮复习

一、解答题

1. (2022·新高考Ⅱ卷) 在某地区进行流行病调查，随机调查了100名某种疾病患者的年龄，得到如下的样本数据频率分布直方图．
1. （1）估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值作代表）；
2. （2）估计该地区一人患这种疾病年龄在区间 $\text{[math]}$ 的概率；
3. （3）已知该地区这种疾病的患病率为0.1%，该地区年龄位于区间 $\text{[math]}$ 的人口占该地区总人口的16%，从该地区任选一人，若此人年龄位于区间 $\text{[math]}$ ，求此人患该种疾病的概率．（样本数据中的患者年龄位于各区间的频率作为患者年龄位于该区间的概率，精确到0.0001）
答案解析收藏纠错 + 选题
2. (2024高二下·浦北期中) 甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得10分，负方得0分，没有平局．三个项目比赛结束后，总得分高的学校获得冠军．已知甲学校在三个项目中获胜的概率分别为0.5，0.4，0.8，各项目的比赛结果相互独立．
1. （1）求甲学校获得冠军的概率；
2. （2）用X表示乙学校的总得分，求X的分布列与期望．
答案解析收藏纠错 + 选题
3. (2022·全国甲卷) 甲、乙两城之间的长途客车均由A和B两家公司运营，为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城之间的500个班次，得到下面列联表：

准点班次数

未准点班次数

A

240

20

B

210

30

附： $\text{[math]}$ ，

$\text{[math]}$

0.100

0.050

0.010

$\text{[math]}$

2.706

3.841

6.635
1. （1）根据上表，分别估计这两家公司甲、乙两城之间的长途客车准点的概率；
2. （2）能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关？
答案解析收藏纠错 + 选题

4. (2023·惠州模拟) 某地经过多年的环境治理，已将荒山改造成了绿水青山．为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位： $\text{[math]}$ ）和材积量（单位： $\text{[math]}$ ），得到如下数据：

样本号i	1	2	3	4	5	6	7	8	9	10	总和
根部横截面积 $\text{[math]}$	0.04	0.06	0.04	0.08	0.08	0.05	0.05	0.07	0.07	0.06	0.6
材积量 $\text{[math]}$	0.25	0.40	0.22	0.54	0.51	0.34	0.36	0.46	0.42	0.40	3.9

并计算得 $\text{[math]}$ ．

附：相关系数 $\text{[math]}$ ．

（1）估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；
（2）求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到0.01）；
（3）现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为 $\text{[math]}$ ．已知树木的材积量与其根部横截面积近似成正比．利用以上数据给出该林区这种树木的总材积量的估计值．

答案解析收藏纠错 + 选题

5. (2022·北京) 在校运动会上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9.50m以上（含9.50m）的同学将获得优秀奖，为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙以往的比赛成绩，并整理得到如下数据（单位：m）：
甲：9.80， 9.70， 9.55， 9.54， 9.48， 9.42， 9.40， 9.35， 9.30， 9.25；

乙：9.78， 9.56， 9.51， 9.36， 9.32， 9.23；

丙：9.85， 9.65， 9.20， 9.16．

假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立

（I）估计甲在校运动会铅球比赛中获得优秀奖的概率；

（II）设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数，估计 $\text{[math]}$ 的数学期望 $\text{[math]}$ ；

（III）在校运动会铅球比赛中，甲、乙、丙谁获得冠军的概率估计值最大？（结论不要求证明）

答案解析收藏纠错 + 选题
6. (2022·新高考Ⅰ卷) 一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系，在己患该疾病的病例中随机调查了100例(称为病例组)，同时在未患该疾病的人群中随机调查了100人(称为对照组)，得到如下数据：

不够良好良好

病例组 40 60

对照组 10 90

附： $\text{[math]}$

P(K² ≥ k)

0.050

0.010

0.001

K

3.841

6.635

10.828
1. （1）能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?
2. （2）从该地的人群中任选一人，A表示事件“选到的人卫生习惯不够良好”，B表示事件“选到的人患有该疾病”， $\text{[math]}$ 与 $\text{[math]}$ 的比值是卫生习惯不够良好对患该
  疾病风险程度的一项度量指标，记该指标为R.
  
  (i)证明： $\text{[math]}$
  
  (ii)利用该调查数据，给出 $\text{[math]}$ 的估计值，并利用(i)的结果给出R的估计值.
答案解析收藏纠错 + 选题
7. (2021·新高考Ⅱ卷) 一种微生物群体可以经过自身繁殖不断生存下来，设一个这种微生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代……，该微生物每代繁殖的个数是相互独立的且有相同的分布列，设X表示1个微生物个体繁殖下一代的个数， $\text{[math]}$ ．
1. （1）已知 $\text{[math]}$ ，求 $\text{[math]}$ ；
2. （2）设p表示该种微生物经过多代繁殖后临近灭绝的概率，p是关于x的方程： $\text{[math]}$ 的一个最小正实根，求证：当 $\text{[math]}$ 时， $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ；
3. （3）根据你的理解说明（2）问结论的实际含义．
答案解析收藏纠错 + 选题
8. (2021高三上·三明月考) 为加快新冠肺炎检测效率，某检测机构采取“k合1检测法”，即将k个人的拭子样本合并检测，若为阴性，则可以确定所有样本都是阴性的；若为阳性，则还需要对本组的每个人再做检测．现有100人，已知其中2人感染病毒．
1. （1） ①若采用“10合1检测法”，且两名患者在同一组，求总检测次数；
  ②已知10人分成一组，分10组，两名感染患者在同一组的概率为 $\text{[math]}$ ，定义随机变量X为总检测次数，求检测次数X的分布列和数学期望E(X)；
2. （2）若采用“5合1检测法”，检测次数Y的期望为E(Y)，试比较E(X)和E(Y)的大小(直接写出结果)．
答案解析收藏纠错 + 选题

9. (2021·全国甲卷) 甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量情况统计如下表：

	一级品	二级品	合计
甲机床	150	50	200
乙机床	120	80	200
合计	270	130	400

（1）甲机床、乙机床生产的产品中一级品的频率分别是多少？
（2）能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?
附： $\text{[math]}$

答案解析收藏纠错 + 选题

10. (2021·全国乙卷) 某厂研究了一种生产高精产品的设备，为检验新设备生产产品的某项指标有无提高，用一台旧设备和一台新设备各生产了10件产品，得到各件产品该项指标数据如下：

旧设备	9.8	10.3	10.0	10.2	9.9	9.8	10.0	10.1	10.2	9.7
新设备	10.1	10.4	10.1	10.0	10.1	10.3	10.6	10.5	10.4	10.5

旧设备和新设备生产产品的该项指标的样本平均数分别记为 $\text{[math]}$ 和 $\text{[math]}$ ，样本方差分别记为s₁²和s₂²

（1）求 $\text{[math]}$ ， $\text{[math]}$ ， s₁² ， s₂²；
（2）判断新设备生产产品的该项指标的均值较旧设备是否有显著提高（如果 $\text{[math]}$ - $\text{[math]}$ ≥ $\text{[math]}$ ，则认为新设备生产产品的该项指标的均值较旧设备有显著提高，否则不认为有显著提高）.

答案解析收藏纠错 + 选题

11. (2021·新高考Ⅰ) 某学校组织"一带一路”知识竞赛，有A，B两类问题・每位参加比赛的同学先在两类问题中选择类并从中随机抽取一个问题冋答，若回答错误则该同学比赛结束；若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束.A类问题中的每个问题回答正确得20分，否则得0分：B类问题中的每个问题回答正确得80分，否则得0分。
已知小明能正确回答A类问题的概率为0.8 ，能正确回答B类问题的概率为0.6.且能正确回答问题的概率与回答次序无关。
1. （1）若小明先回答A类问题，记X为小明的累计得分，求X的分布列：
2. （2）为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由。
答案解析收藏纠错 + 选题

12. (2020·新课标Ⅲ·理) 某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：

锻炼人次空气质量等级	[0，200]	(200，400]	(400，600]
1（优）	2	16	25
2（良）	5	10	12
3（轻度污染）	6	7	8
4（中度污染）	7	2	0

附： $\text{[math]}$ ，

P(K²≥k)	0.050	0.010	0.001
k	3.841	6.635	10.828

（1）分别估计该市一天的空气质量等级为1，2，3，4的概率；
（2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；
（3）若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？

人次≤400

人次>400

空气质量好

空气质量不好

答案解析收藏纠错 + 选题

13. (2020·新课标Ⅱ·文) 某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加.为调查该地区某种野生动物的数量，将其分成面积相近的200个地块，从这些地块中用简单随机抽样的方法抽取20个作为样区，调查得到样本数据(x_i ， y_i)(i=1，2，…，20)，其中x_i和y_i分别表示第i个样区的植物覆盖面积(单位：公顷)和这种野生动物的数量，并计算得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求该地区这种野生动物数量的估计值（这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数）；
2. （2）求样本(x_i ， y_i)(i=1，2，…，20)的相关系数（精确到0.01）；
3. （3）根据现有统计资料，各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由.
  附：相关系数r= $\text{[math]}$ ， $\text{[math]}$ =1.414.
答案解析收藏纠错 + 选题
14. (2020·新课标Ⅰ·理) 甲、乙、丙三位同学进行羽毛球比赛，约定赛制如下：累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束.经抽签，甲、乙首先比赛，丙轮空.设每场比赛双方获胜的概率都为 $\text{[math]}$ ，
1. （1）求甲连胜四场的概率；
2. （2）求需要进行第五场比赛的概率；
3. （3）求丙最终获胜的概率.
答案解析收藏纠错 + 选题

15. (2020高二下·永泰期末) 为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的 $\text{[math]}$ 和 $\text{[math]}$ 浓度（单位： $\text{[math]}$ ），得下表：

$\text{[math]}$ $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

$\text{[math]}$	32	18	4
$\text{[math]}$	6	8	12
$\text{[math]}$	3	7	10

附： $\text{[math]}$ ，

$\text{[math]}$	0.050 0.010 0.001
$\text{[math]}$	3.841 6.635 10.828

（1）估计事件“该市一天空气中 $\text{[math]}$ 浓度不超过75，且 $\text{[math]}$ 浓度不超过150”的概率；
（2）根据所给数据，完成下面的 $\text{[math]}$ 列联表：

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$
（3）根据（2）中的列联表，判断是否有 $\text{[math]}$ 的把握认为该市一天空气中 $\text{[math]}$ 浓度与 $\text{[math]}$ 浓度有关？

答案解析收藏纠错 + 选题

16. (2020·北京) 某校为举办甲、乙两项不同活动，分别设计了相应的活动方案：方案一、方案二．为了解该校学生对活动方案是否支持，对学生进行简单随机抽样，获得数据如下表：

	男生		女生
	支持	不支持	支持	不支持
方案一	200人	400人	300人	100人
方案二	350人	250人	150人	250人

假设所有学生对活动方案是否支持相互独立．

（Ⅰ）分别估计该校男生支持方案一的概率、该校女生支持方案一的概率；

（Ⅱ）从该校全体男生中随机抽取2人，全体女生中随机抽取1人，估计这3人中恰有2人支持方案一的概率；

（Ⅲ）将该校学生支持方案的概率估计值记为 $\text{[math]}$ ，假设该校年级有500名男生和300名女生，除一年级外其他年级学生支持方案二的概率估计值记为 $\text{[math]}$ ，试比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小．（结论不要求证明）

答案解析收藏纠错 + 选题

17. (2019·江苏) 在平面直角坐标系xOy中，设点集 $\text{[math]}$ ， $\text{[math]}$
令 $\text{[math]}$ .从集合M_n中任取两个不同的点，用随机变量X表示它们之间的距离.
1. （1）当n=1时，求X的概率分布；
2. （2）对给定的正整数n（n≥3），求概率P（X≤n）（用n表示）.
答案解析收藏纠错 + 选题

18. (2019·天津) 2019年，我国施行个人所得税专项附加扣除办法，涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有 $\text{[math]}$ 人，现采用分层抽样的方法，从该单位上述员工中抽取25人调查专项附加扣除的享受情况.

（Ⅰ）应从老、中、青员工中分别抽取多少人？

（Ⅱ）抽取的25人中，享受至少两项专项附加扣除的员工有6人，分别记为 $\text{[math]}$ .享受情况如右表，其中“ ”表示享受，“×”表示不享受.现从这6人中随机抽取2人接受采访.

员工项目	A	B	C	D	E	F
子女教育	○	○	×	○	×	○
继续教育	×	×	○	×	○	○
大病医疗	×	×	×	○	×	×
住房贷款利息	○	○	×	×	○	○
住房租金	×	×	○	×	×	×
赡养老人	○	○	×	×	×	○

（i）试用所给字母列举出所有可能的抽取结果；

（ii）设 $\text{[math]}$ 为事件“抽取的2人享受的专项附加扣除至少有一项相同”，求事件 $\text{[math]}$ 发生的概率.

答案解析收藏纠错 + 选题

19. (2022高二下·合肥期中) 设甲、乙两位同学上学期间，每天7：30之前到校的概率均为 $\text{[math]}$ .假定甲、乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立.
（Ⅰ）用 $\text{[math]}$ 表示甲同学上学期间的三天中7：30之前到校的天数，求随机变量 $\text{[math]}$ 的分布列和数学期望；

（Ⅱ）设 $\text{[math]}$ 为事件“上学期间的三天中，甲同学在7：30之前到校的天数比乙同学在7：30之前到校的天数恰好多2”，求事件 $\text{[math]}$ 发生的概率.

答案解析收藏纠错 + 选题
20. (2020高二上·贵港期中) 为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液，每只小鼠给服的溶液体积相同、摩尔浓度相同。经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：

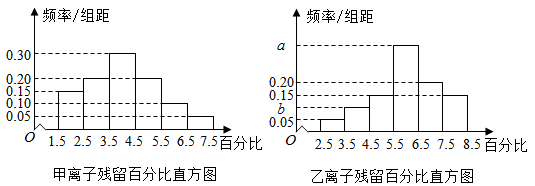
记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P（C）的估计值为0.70.
1. （1）求乙离子残留百分比直方图中a，b的值；
2. （2）分别估计甲，乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）
答案解析收藏纠错 + 选题
21. (2020高二下·唐山期中) 11分制乒乓球比赛，每赢一球得1分，当某局打成10：10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束.甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立.在某局双方10：10平后，甲先发球，两人又打了X个球该局比赛结束.
1. （1）求P（X=2）；
2. （2）求事件“X=4且甲获胜”的概率.
答案解析收藏纠错 + 选题
22. (2019·北京) 改革开放以来，人们的支付方式发生了巨大转变.近年来，移动支付已成为主要支付方式之一.为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校所有的1000名学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额

支付方式

不大于2000元

大于2000元

仅使用A

27人

3人

仅使用B

24人

1人

（I）估计该校学生中上个月A，B两种支付方式都使用的人数；

（II）从样本仅使用B的学生中随机抽取1人，求该学生上个月支付金额大于2000元的概率；

（III）已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中，随机抽查1人，发现他本月的支付金额大于2000元，结合（II）的结果，能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化？说明理由.

答案解析收藏纠错 + 选题

23. (2019·北京) 改革开放以来，人们的支付方式发生了巨大转变。近年来，移动支付已成为主要支付方式之一。为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额（元）

支付方式

（0，1000]

（1000，2000]

大于2000

仅使用A

18人

9人

3人

仅使用B

10人

14人

1人

（I）从全校学生中随机抽取1人，估计该学生上个月A，B两种支付方式都使用的概率；

（II）从样本仅使用A和仅使用B的学生中各随机抽取1人，以X表示这2人中上个月支付金额大于1000元的人数，求X的分布列和数学期望；

（III）已知上个月样本学生的支付方式在本月没有变化。现从样本仅使用A的学生中，随机抽查3人，发现他们本月的支付金额都大于2000元，根据抽查结果，能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化？说明理由.

答案解析收藏纠错 + 选题

24. (2019·全国Ⅰ卷理) 为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验。试验方案如下：每一轮选取两只白鼠对药效进行对比试验。对于两只白鼠，随机选一只施以甲药，另一只施以乙药。一轮的治疗结果得出后，再安排下一轮试验。当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效。为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分：若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分：若都治愈或都未治愈则两种药均得0分。甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X。
1. （1）求X的分布列；
2. （2）若甲药、乙药在试验开始时都赋予4分，p_i(i=0，1，…，8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效“的概率，则P₀=0，P₈=1，p_i=ap_i-1+bp_i+cp_i+1(i=1，2，…，7)，其中a=P(X=-1)，b=P(X=0)，c=P(X=1)。假设α=0.5，β=0.8。
  (i)证明： $\text{[math]}$ （i=0，1，2，…，7）为等比数列；
  
  (ii)求P₄ ，并根据P₄的值解释这种试验方案的合理性。
答案解析收藏纠错 + 选题
25. (2018·全国Ⅰ卷理) 某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品，检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验。设每件产品为不合格的概率为品p（ $\text{[math]}$ ），且各件产品是否为不合格品相互独立。
1. （1）记20件产品中恰有2件不合格品的概率为 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值点 $\text{[math]}$
2. （2）现对一箱产品检验了20件，结果恰有2件不合格品，以（1）中确定的 $\text{[math]}$ 作为 $\text{[math]}$ 的值。已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用
  (i)若不对该箱余下的产品作检验，这一箱的检验费用与赔偿费用的和记为 $\text{[math]}$ ，求 $\text{[math]}$ ；
  (ii)以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？
答案解析收藏纠错 + 选题
26. (2018·天津) 已知某单位甲、乙、丙三个部门的员工人数分别为24，16，16.现采用分层抽样的方法从中抽取7人，进行睡眠时间的调查.
（Ⅰ）应从甲、乙、丙三个部门的员工中分别抽取多少人？
（Ⅱ）若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查.
（i）用X表示抽取的3人中睡眠不足的员工人数，求随机变量X的分布列与数学期望；
（ii）设A为事件“抽取的3人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件A发生的概率.

答案解析收藏纠错 + 选题
27. (2018·天津) 已知某校甲、乙、丙三个年级的学生志愿者人数分别为240，160，160．现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动．
（Ⅰ）应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人？
（Ⅱ）设抽出的7名同学分别用A ， B ， C ， D ， E ， F ， G表示，现从中随机抽取2名同学承担敬老院的卫生工作．
（i）试用所给字母列举出所有可能的抽取结果；
（ii）设M为事件“抽取的2名同学来自同一年级”，求事件M发生的概率．

答案解析收藏纠错 + 选题
28. (2018·全国Ⅱ卷理) 下图是某地区2000年至2016年环境基础设施投资额 $\text{[math]}$ (单位：亿元)的折线图。
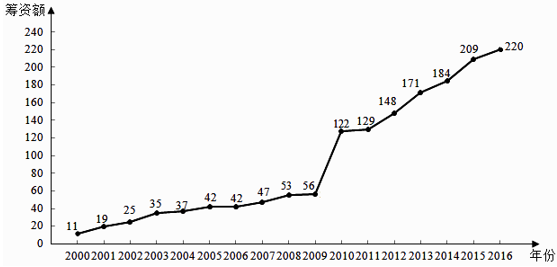
为了预测该地区2018年的环境基础设施投资额，建立了 $\text{[math]}$ 与时间变量t的两个线性回归模型，根据2000年至2016年的数据（时间变量 $\text{[math]}$ 的值依次为1，2，…….，17）建立模型①： $\text{[math]}$ .根据2010年至2016年的数据（时间变量t的值依次为1，2，…，7）建立模型②： $\text{[math]}$
1. （1）分别利用这两个模型，求该地区2018年的环境基础设施投资的预测值；
2. （2）你认为用哪个模型得到的预测值更可靠？并说明理由。
答案解析收藏纠错 + 选题
29. (2018·全国Ⅲ卷理) 某工厂为提高生产效率，开展技术创新活动，提出了完成项目生产任务的两种新的生产方式，为比较两种生产方式的效率，选取40名工人，将他们随即分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式，根据工人完成生产任务的工作时间(单位：min)绘制了如下茎叶图：
1. （1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；
2. （2）求40名工人完成生产任务所需时间的中位数m，并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表：
  
  超过m
  不超过m
  第一种生产方式
  
  第二种生产方式
3. （3）根据2中的列联表，能否有99%的把握认为两种生产方式的效率有差异？
  附： $\text{[math]}$ ，
答案解析收藏纠错 + 选题
30. (2018·北京) 电影公司随机收集了电影的有关数据，经分类整理得到下表：
电影类型
第一类
第二类
第三类
第四类
第五类
第六类
电影部数
140
50
300
200
800
510
好评率
0.4
0.2
0.15
0.25
0.2
0.1
好评率是指：一类电影中获得好评的部数与该类电影的部数的比值
假设所有电影是否获得好评相互独立。
（Ⅰ）从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影的概率；
（Ⅱ）从第四类电影和第五类电影中各随机选取1部，估计恰有1部获得好评的概率；
（Ⅲ）假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等，用“ $\text{[math]}$ ”表示第k类电影得到人们喜欢，“ $\text{[math]}$ ”表示第k类电影没有得到人们喜欢（k=1，2，3，4，5，6），写出方差 $\text{[math]}$ 的大小关系。

答案解析收藏纠错 + 选题
31. (2018·北京) 电影公司随机收集了电影的有关数据，经分类整理得到下表：
电影类型
第一类
第二类
第三类
第四类
第五类
第六类
电影部数
140
50
300
200
800
510
好评率
0.4
0.2
0.15
0.25
0.2
0.1
好评率是指：一类电影中获得好评的部数与该类电影的部数的比值.
（Ⅰ）从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影的概率；
（Ⅱ）随机选取1部电影，估计这部电影没有获得好评的概率；
（Ⅲ）电影公司为增加投资回报，拟改变投资策略，这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化，那么哪类电影的好评率增加0.1，哪类电影的好评率减少0.1，使得获得好评的电影总部数与样本中的电影总部数的比值达到最大？（只需写出结论）

答案解析收藏纠错 + 选题

试卷信息