


≌
;
;
求证: .
请将下面的推理过程补充完整:
证明:如图 , 延长
到点
, 使
, 连接
.
∵是
的中线,
∴ .
在和
中,
,
∴( ).
∴ ▲ (全等三角形的对应边相等).
∴在中,
( ),
∴ .
即 .

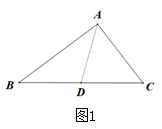
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE,容易证得△ADC≌△EDB,再由“三角形的三边关系”可求得AD的取值范围是.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.


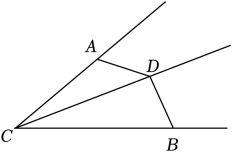
试猜测
和
的数量关系,并说明理由;
若
的面积为5,求四边形
的面积.
①已知点是网格中的格点,若三角形
是以
为底边的等腰三角形,那么这样的
点共有 ▲ 个;
②在网格中找出一个点 , 使得点
到点
,
和点
,
的距离分别相等,请在网格中标注点
保留作图痕迹

如图1,在中,
,
, 直线
经过点
, 且
、
两点在直线
的同侧,
直线
,
直线
, 垂足分别为点
,
. 请直接写出
、
和
的数量关系.
如图2,在(1)的条件下,若 ,
两点在直线
的异侧,请说明
、
和
的关系,并证明.
如图3,在(1)的条件下,若三个直角都变为了相等的钝角,即 , 其中
, (1)的结论还成立吗?若成立,请你给出证明;若不成立,请说明
、
和
的关系,并证明.
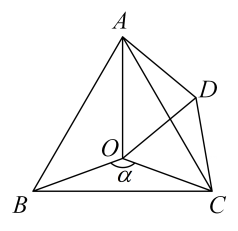
小芮同学探究此问题的方法是:延长到点G,使
. 连接
, 先证明
, 再证明
, 可得出结论,他的结论应是;




②如图2,若五边形的面积为30,
,
, 直接写出
点到
的距离.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接CG,先证明CBE≌
CDG,再证明
CEF≌
CGF.他得出的正确结论是 .

证明:∵是等边三角形,∴
.
∵ ,
, ∴
.
∴ ,
.
∵ , ∴
.
即 ;

∴把△ABE绕点A逆时针旋转90°至△ADE',则F、D、E'在一条直线上,
∠E'AF=度,……
根据定理,可证:△AEF≌△AE'F.
∴EF=BE+DF.
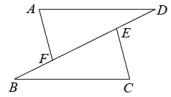
如图1,已知
, 连结
, 求证:
.
如图2,已知
平分
, 求证:
.