
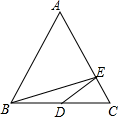


①若 ,
, 则四边形
是平行四边形;
②若 ,
, 则四边形
是平行四边形;
③若 ,
, 则四边形
是平行四边形;
④若 ,
, 则四边形
是平行四边形.
其中正确的结论是.(写出所有正确结论的序号)



(1)的三个顶点都在格点上.
在图1中,画出一个与
成中心对称的格点三角形;
在图2中,画出
绕着点
按顺时针方向旋转
后的三角形.
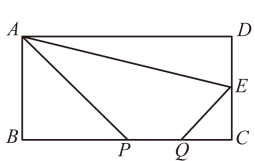
(2)如图3是由5个边长为1的小正方形拼成的图形,请用无刻度的直尺画经过点的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
(要求:在给出的△ABC中用尺规作出AB、AC边的中点M、N , 保留作图痕迹,不要求写作法,并根据图形写出已知、求证和证明)
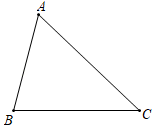



请你写出证明过程.
问题情境:已知,如图1,在Rt△ABC中,∠ACB=90°,AC=BC=4.点D是AC的中点,点E在BC延长线上,且∠CDE=60°.保持△ABC不动,将△CDE从图1的位置开始,绕点C顺时针旋转α°(0<α<180)得到△CD'E',D、E的对应点分别为D'、E'.


A.在△CDE旋转过程中,当D'E'//BC时,请直接写出此时旋转角a的度数及B、E'两点间的距离.
B.在△CDE旋转过程中,当D'E'//AB时,延长AC交D'E'于点F,请直接写出此时旋转角α的度数及线段CF的长.


问题解决: