浙教版数学九年级上学期期末重难点复习：二次函数难题汇总卷

更新时间：2023-04-07 浏览次数：31 类型：复习试卷

一、第一节内容

1. 已知菱形ABCD的边长为1，∠DAB=60°，E为AD上的动点，F在CD上，且AE+CF=1，设ΔBEF的面积为y，AE=x，当点E运动时，能正确描述y与x关系的图像是：（）

A . B . C . D .

答案解析收藏纠错 + 选题
2.
如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·富顺期中) 如图所示，已知抛物线在坐标系中的顶点为 $\text{[math]}$ ，且与坐标轴交点为 $\text{[math]}$ 点.（相关数据见图中标示）
1. （1）求该抛物线的解析式；
2. （2）求△ $\text{[math]}$ 的面积；
3. （3）在 $\text{[math]}$ 轴上求作一点 $\text{[math]}$ 使△ $\text{[math]}$ 得周长最小，求出满足条件的点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
4. (2021九上·连山月考) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ 、 $\text{[math]}$ ．且点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为抛物线上的一动点．
1. （1）求二次函数的解析式；
2. （2）如图1，过点 $\text{[math]}$ 作 $\text{[math]}$ 平行于 $\text{[math]}$ 轴，交抛物线于点 $\text{[math]}$ ，若点 $\text{[math]}$ 在 $\text{[math]}$ 的上方，作 $\text{[math]}$ 平行于 $\text{[math]}$ 轴交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 时，求点 $\text{[math]}$ 坐标；
3. （3）设抛物线的对称轴与 $\text{[math]}$ 交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，当以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的四边形为平行四边形时，请直接写出点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
5. (2021九上·海州期末) 已知抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ ，与y轴交于点C，顶点为点D.
1. （1）求抛物线的解析式；
2. （2）若点P在抛物线上，点Q在x轴上，当以点A、C、P、Q为顶点的四边形是平行四边形时，请直接写出点P的坐标；
3. （3）已知点 $\text{[math]}$ ， $\text{[math]}$ ，在抛物线对称轴上，找一点F，使 $\text{[math]}$ 的值最小.此时，在抛物线上是否存在一点K，使 $\text{[math]}$ 的值最小？若存在，求出点K的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
6. (2021九上·虎林期末) 如图，抛物线y=ax² + bx + c 交x轴于A、B两点，交y轴于点C，对称轴为直线x=1，已知：A(-1，0)、C(0，-3).
1. （1）求抛物线y= ax² + bx + c 的解析式；
2. （2）求△AOC和△BOC的面积比；
3. （3）在对称轴上是否存在一个P点，使△PAC的周长最小.若存在，请你求出点P的坐标；若不存在，请你说明理由.
答案解析收藏纠错 + 选题
7. (2020九上·福山月考) 如图，在坐标系xOy中，△ABC是等腰直角三角形，∠BAC＝90°，A（1，0），B（0，2），抛物线y＝ $\text{[math]}$ x²+bx﹣2的图象过C点．
1. （1）求抛物线的解析式；
2. （2）平移该抛物线的对称轴所在直线l，当l移动到何处时，恰好将△ABC的面积分为相等的两部分？
答案解析收藏纠错 + 选题
8. (2020九上·官渡期末) 如图①，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．
1. （1）求抛物线 $\text{[math]}$ 的解析式；
2. （2）如图②，连接 $\text{[math]}$ ，点 $\text{[math]}$ 是第三象限内抛物线上的动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 轴交 $\text{[math]}$ 于点 $\text{[math]}$ ，求 $\text{[math]}$ 面积的最大值及此时点 $\text{[math]}$ 的坐标；
3. （3）如图③，若抛物线的顶点坐标为点 $\text{[math]}$ ，点 $\text{[math]}$ 是抛物线对称轴上的动点，在坐标平面内是否存在点 $\text{[math]}$ ，使得以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是菱形?若存在，求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
9. (2018九上·孝感月考) 甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在 $\text{[math]}$ 点上正方 $\text{[math]}$ 的 $\text{[math]}$ 处发出一球，羽毛球飞行的高度 $\text{[math]}$ 与水平距离 $\text{[math]}$ 之间满足函数表达式 $\text{[math]}$ ．已知点 $\text{[math]}$ 与球网的水平距离为 $\text{[math]}$ ，球网的高度为 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，①求 $\text{[math]}$ 的值；
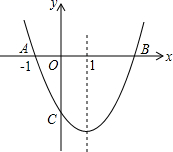
  ②通过计算判断此球能否过网；
2. （2）若甲发球过网后，羽毛球飞行到 $\text{[math]}$ 处时，乙扣球成功。已知点 $\text{[math]}$ 离点 $\text{[math]}$ 的水平距离为 $\text{[math]}$ ，离地面的高度为 $\text{[math]}$ 的，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题

二、第二节内容

10. (2022九上·通榆期中) 已知抛物线y=-x²+bx+c(b，c为常数)经过点(0，-3)、(-6，-3)．
1. （1）求此抛物线的解析式．
2. （2）此抛物线的顶点坐标为
3. （3）当-4≤x≤0时，求y的最大值和最小值．
4. （4）当m≤x≤0时，若y的最大值与最小值之和为2，直接写出m的值．
答案解析收藏纠错 + 选题
11. (2022九上·温州月考) 在平面直角坐标系中，二次函数 $\text{[math]}$ （ $\text{[math]}$ ， m为常数）的图象记作G，图象G上点A的横坐标为2m．
1. （1）当 $\text{[math]}$ ，求图象G的最低点坐标；
2. （2）平面内有点 $\text{[math]}$ ．当AC不与坐标轴平行时，以AC为对角线构造矩形ABCD，AB与x轴平行，BC与y轴平行．
  ①若矩形ABCD为正方形时，求点A坐标；
  ②图象G与矩形ABCD的边有两个公共点时，求m的取值范围．
答案解析收藏纠错 + 选题
12. (2022·云南) 已知抛物线 $\text{[math]}$ 经过点（0，2），且与 $\text{[math]}$ 轴交于A、B两点．设k是抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交点的横坐标；M是抛物线 $\text{[math]}$ 的点，常数m>0，S为△ABM的面积．已知使S=m成立的点M恰好有三个，设T为这三个点的纵坐标的和．
1. （1）求c的值；
2. （2）且接写出T的值；
3. （3）求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
13. (2022·巴中) 函数 $\text{[math]}$ 的图象是由函数 $\text{[math]}$ 的图象 $\text{[math]}$ 轴上方部分不变，下方部分沿 $\text{[math]}$ 轴向上翻折而成，如图所示，则下列结论正确的是（）
① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④将图象向上平移1个单位后与直线 $\text{[math]}$ 有3个交点．

A . ①② B . ①③ C . ②③④ D . ①③④

答案解析收藏纠错 + 选题
14. (2022·二道模拟) 在平面直角坐标系中，已知抛物线 $\text{[math]}$ （m为常数）.
1. （1）求此抛物线的顶点坐标.（用含m的式子表示）
2. （2）当 $\text{[math]}$ 时，抛物线对应的函数值y随x的增大而先增大后减小，求m的取值范围.
3. （3）将抛物线 $\text{[math]}$ （m为常数）在y轴右侧的部分沿着直线 $\text{[math]}$ 翻折，翻折后的图像与原抛物线剩余部分合称为图像G.
  ①当 $\text{[math]}$ 时，在如图的平面直角坐标系中画出图像G.
  ②当 $\text{[math]}$ ，且图像G与直线 $\text{[math]}$ 有且只有两个公共点时，求这两个公共点之间的距离.
  ③正方形 $\text{[math]}$ 的顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，顶点B的坐标为 $\text{[math]}$ ，当图像G和正方形 $\text{[math]}$ 的边有且只有四个公共点时，直接写出m的取值范围.
答案解析收藏纠错 + 选题
15. (2022·石城模拟) 若平面直角坐标系内的点 $\text{[math]}$ 满足横、纵坐标都为整数，则把点 $\text{[math]}$ 叫做“整点”．例如： $\text{[math]}$ 、 $\text{[math]}$ 都是“整点”．抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于A、 $\text{[math]}$ 两点，若该抛物线在A、 $\text{[math]}$ 之间的部分与线段 $\text{[math]}$ 所围成的区域(包括边界)恰有七个整点，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2022·岐山模拟) 已知抛物线 $\text{[math]}$ 与y轴的交点为A，顶点为P，对称轴为直线m.
1. （1）求抛物线l的顶点坐标P和对称轴.
2. （2）抛物线l关于点A对称的抛物线为 $\text{[math]}$ ，抛物线 $\text{[math]}$ 的顶点为Q，对称轴为直线n，在直线m和直线n上是否分别存在点E、F，使得四边形 $\text{[math]}$ 为正方形？若存在，请求出a的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
17. (2021九上·上思期中) 如图所示，已知二次函数y=ax²+bx+c的图象与x轴交于A、B两点，与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax²+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：
①2a+b+c＞0；②a﹣b+c＜0；③x（ax+b）≤a+b；④a＜﹣1.

其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
18. (2021九上·温岭期中) 如图，已知二次函数y=ax²+bx+c的图象与x轴交于点（-2，0）、（x₁ ， 0），且1<x₁ <2，与y轴交于正半轴.下列结论错误的是（）

A . 4a-2b+c=0 B . 当x< $\text{[math]}$ 时，y随x增大而增大 C . 当x> $\text{[math]}$ 时，y随x增大而减小 D . a<b<0

答案解析收藏纠错 + 选题
19. (2021九上·诸暨月考) 定义：如果两个函数y₁ ， y₂存在x取同一个值，使得y₁＝y₂ ，那么称y₁ ， y₂互为“等值函数”，对应的x值为y₁ ， y₂的“等值根”．
1. （1）函数y₁＝ $\text{[math]}$ x+b与 $\text{[math]}$ 是否互为“等值函数”？如果是，求出当b＝1时，两函数的“等值根”；如果不是，请说明理由．
2. （2）如图所示的是y＝﹣|x²+2x|的图象，它是由二次函数y＝﹣x²﹣2x的图象x轴上方的部分沿x轴翻折到x轴下方，图象的其余部分保持不变得到的．若y₁＝ $\text{[math]}$ x+b与y₂＝﹣|x²+2x|互为“等值函数”，且有两个“等值根”，求b的取值范围．
答案解析收藏纠错 + 选题
20. (2021九上·诸暨月考) 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，对称轴为直线x＝﹣1，下列结论不正确的是（）

A . b²＞4ac B . abc＞0 C . a﹣c＜0 D . am²+bm≥a﹣b（m为为任意实数）

答案解析收藏纠错 + 选题
21. (2021九上·南部月考) 如图，抛物线G：y₁＝a（x+1）²+2与H：y₂＝﹣（x﹣2）²﹣1交于点B(1，﹣2)，且分别与y轴交于点D、E．过点B作x轴的平行线，交抛物线于点A、C，则以下结论：①无论x取何值，y₂总是负数；②抛物线H可由抛物线G向右平移3个单位，再向下平移3个单位得到；③当﹣3＜x＜1时，随着x的增大，y₁﹣y₂的值先增大后减小；④四边形AECD为正方形．其中正确的是（　　）

A . ①③④ B . ①②④ C . ②③④ D . ①②③④

答案解析收藏纠错 + 选题

三、第三四节

22. (2024九下·凉州模拟) $\text{[math]}$ 关于 $\text{[math]}$ 的二次函数 $\text{[math]}$ ，在 $\text{[math]}$ 时有最大值6，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
23. (2023·合川九上期末) 已知抛物线 $\text{[math]}$ 的图象与x轴相交于点A和点 $\text{[math]}$ ，与y轴交于点C，连接AC，有一动点D在线段AC上运动，过点D作x轴的垂线，交抛物线于点E，交x轴于点F， $\text{[math]}$ ，设点D的横坐标为m.
1. （1）连接AE，CE则 $\text{[math]}$ 的最大面积为；
2. （2）当 $\text{[math]}$ 时，在平面内存在点Q，使以B，C，E，Q为顶点的四边形为平行四边形，请写出点Q的坐标.
答案解析收藏纠错 + 选题
24. (2022九上·江城期末) 二次函数 $\text{[math]}$ 的部分图象如图所示，其对称轴为直线 $\text{[math]}$ ，且与 $\text{[math]}$ 轴的一个交点坐标为 $\text{[math]}$ ，下列结论：
① $\text{[math]}$ ；② $\text{[math]}$ ；③图象与 $\text{[math]}$ 轴的另一个交点坐标为 $\text{[math]}$ ；④关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个相等的实数根；⑤ $\text{[math]}$ ．其中正确的结论个数是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
25. (2022九上·莱州期末) 如图，抛物线 $\text{[math]}$ 交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．

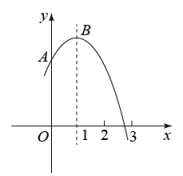
①一元二次方程 $\text{[math]}$ 有两个相等的实数根；②若点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在该函数图象上，则 $\text{[math]}$ ；③将该抛物线先向左平移1个单位，再沿x轴翻折，得到的抛物线表达式是 $\text{[math]}$ ；④在y轴上找一点D，使 $\text{[math]}$ 的面积为1，则D点的坐标为 $\text{[math]}$ .以上四个结论中正确的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
26. (2022九上·莒南期中) 若任意两个正数的和为定值，则它们的乘积会如何变化呢？会不会存在最大值？
特例研究：若两个正数的和是1，那么这两个正数可以是： $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ ， …

由于这样的正数有很多，我们不妨设其中一个正数是 $\text{[math]}$ ，另外一个正数为 $\text{[math]}$ ，那么 $\text{[math]}$ ，则 $\text{[math]}$ ，所以 $\text{[math]}$ ， $\text{[math]}$ ，可以看出两数的乘积 $\text{[math]}$ 是 $\text{[math]}$ 的二次函数，乘积的最大值转化为求关于 $\text{[math]}$ 的二次函数的最值问题．

方法迁移：
1. （1）若两个正数x和y的和是6，其中一个正数为 $\text{[math]}$ ，这两个正数的乘积为z，写出z与x的函数关系式，并画出函数图象．
2. （2）在（1）的条件下，z的最大值为：，并写出此时函数图象的至少一个性质．
3. （3）问题解决：
  由以上题目可知若任意两个正数的和是一个固定的数，那么这两个正数的乘积存在最大值，即对于正数x，y，若x+y是定值，则xy存在最大值．
  
  类比应用：
  
  利用上面所得到的结论，完成填空：
  
  ①已知函数 $\text{[math]}$ 与函数 $\text{[math]}$ ，则当x＝时， $\text{[math]}$ 取得最大值为；
  
  ②已知函数y₁＝2x-2+m（x≥1），m为正定值，函数y₂＝-2x+8（x<4），则当x为何值时， $\text{[math]}$ 取得最大值，最大值是多少？
答案解析收藏纠错 + 选题
27. (2022九上·舟山期中) 已知关于 $\text{[math]}$ 的二次函数 $\text{[math]}$ ，其中 $\text{[math]}$ 为实数，当-2≤x≤1时， $\text{[math]}$ 的最小值为4，满足条件的 $\text{[math]}$ 的值为。

答案解析收藏纠错 + 选题
28. (2021九上·长春期末) 已知抛物线 $\text{[math]}$ 有最高点．
1. （1） m0（填“>、=、<”）；
2. （2）求二次函数 $\text{[math]}$ 的最大值（用含m的式子表示）；
3. （3）将抛物线G向右平移m个单位得到抛物线 $\text{[math]}$ ．经过探究发现，随着m的变化，抛物线 $\text{[math]}$ 顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；
4. （4）记（3）所求的函数为H，抛物线G与函数H的图象交于点P，结合图象，求点P的纵坐标 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
29. (2022九上·鹿城期末) 已知函数 $\text{[math]}$ ， $\text{[math]}$ 在同一平面直角坐标系中.
1. （1）若 $\text{[math]}$ 经过点（1，-2），求 $\text{[math]}$ 的函数表达式.
2. （2）若 $\text{[math]}$ 经过点（1，m+1），判断 $\text{[math]}$ 与 $\text{[math]}$ 图象交点的个数，说明理由.
3. （3）若y₁经过点（ $\text{[math]}$ ， 0)，且对任意x，都有 $\text{[math]}$ ，请利用图象求a的取值范围.
答案解析收藏纠错 + 选题
30. (2023九上·大冶期末) 抛物线 $\text{[math]}$ 与坐标轴分别交于A，B，C三点，P是第一象限内抛物线上的一点.
1. （1）直接写出A，B，C三点的坐标为A，B，C；
2. （2）连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，求点P的坐标；
3. （3）连接 $\text{[math]}$ ， $\text{[math]}$ ，是否存在点P，使得 $\text{[math]}$ ，若存在，求出点P的坐标，若不存在，请说明理由.
答案解析收藏纠错 + 选题