人教版八年级下数学期末复习知识点扫盲满分计划——17.1勾股...

更新时间：2023-05-18 浏览次数：54 类型：复习试卷

一、用勾股定理解三角形

1. (2023八下·杭州期中) 如图，在△ABC中，点D，E分别是AB，AC的中点，连结BE，若AE＝6，DE＝5，∠BEC＝90°，则BE＝.

答案解析收藏纠错 + 选题
2. (2022八上·武义期末) 如图，在△ABC中，AB＝AC，D，E是△ABC内两点，AD平分∠BAC，∠EBC＝∠BEC＝67.5°，BD＝1，则BC＝.

答案解析收藏纠错 + 选题
3. 如图所示，△ABC是等边三角形，P是∠ABC的平分线BD上一点，PE⊥AB于点E，线段BP的垂直平分线交BC于点F，垂足为点Q．若BF=2，则PE的长为（）

A . 2 B . 2 $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
4. (2017八下·凉山期末) 在Rt△ABC，∠BAC=90°，AB=8，AC=6，DE是AB边的垂直平分线，垂足为D，交边BC于点E，连结AE，则△ACE的周长是（）

A . 8 B . 10 C . 14 D . 16

答案解析收藏纠错 + 选题
5. (2022·义乌模拟) 如图，在等边三角形ABC中，AB=8，点P是BC边上的动点，点P关于直线AB、AC的对称点分别为M、N，作 $\text{[math]}$ ，垂足为D，作 $\text{[math]}$ ，垂足为E，则DE的长为（）

A . 10 B . $\text{[math]}$ C . 11 D . 12

答案解析收藏纠错 + 选题

二、已知两点坐标求两点距离

6. (2021八下·黟县期末) 阅读下列一段文字，然后回答下列问题．
已知平面内两点 M（x1，y1）、N（x2，y2），则这两点间的距离可用下列公式计算： MN= $\text{[math]}$ ．

例如：已知 P（3，1）、Q（1，﹣2），则这两点间的距离 PQ= $\text{[math]}$ = $\text{[math]}$ ．

特别地，如果两点 M（x1，y1）、N（x2，y2）所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴，那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨．
1. （1）已知 A（1，2）、B（﹣2，﹣3），试求 A、B 两点间的距离；
2. （2）已知 A、B 在平行于 x 轴的同一条直线上，点 A 的横坐标为 5，点 B 的横坐标为﹣1，
  试求 A、B 两点间的距离；
3. （3）已知△ABC 的顶点坐标分别为 A（0，4）、B（﹣1，2）、C（4，2），你能判定△ABC 的形状吗？请说明理由．
答案解析收藏纠错 + 选题
7. (2020八上·银川期中) 先阅读下列一段文字，再回答后面的问题：已知在平面直角坐标系内两点 $\text{[math]}$ ，其两点间的距离 $\text{[math]}$ ，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为 $\text{[math]}$ 或 $\text{[math]}$ .
1. （1）已知 $\text{[math]}$ ，试求 $\text{[math]}$ 两点间的距离；
2. （2）已知线段 $\text{[math]}$ 轴， $\text{[math]}$ ，若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，试求点 $\text{[math]}$ 的坐标；
3. （3）已知一个三角形各顶点坐标为 $\text{[math]}$ ，你能判定此三角形的形状吗？说明理由.
答案解析收藏纠错 + 选题
8. (2020八下·古冶期中) 如图，在直角坐标系中，有两点 $\text{[math]}$ 和 $\text{[math]}$ ，则这两点之间的距离是（）

A . $\text{[math]}$ B . 13 C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
9. (2019七下·十堰期末) 先阅读下列一段文字，再解答问题：
已知在平面内有两点 $\text{[math]}$ ， $\text{[math]}$ ，其两点间的距离公式为 $\text{[math]}$ ；同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为 $\text{[math]}$ 或 $\text{[math]}$ .
1. （1）已知点A（2，4），B（-2，1），则AB=；
2. （2）已知点C，D在平行于y轴的直线上，点C的纵坐标为4，点D的纵坐标为-2，则CD=；
3. （3）已知点P（3，1）和（1）中的点A，B，判断线段PA，PB，AB中哪两条线段的长是相等的？并说明理由.
答案解析收藏纠错 + 选题
10. (2019八上·梅列期中) 认真阅读下列材料，然后完成解答：
（材料）

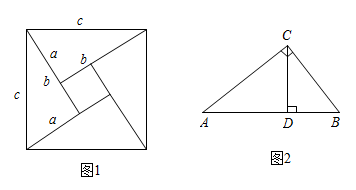
如图，已知平面直角坐标系中两点A（x₁ ， y₁）、B（x₂ ， y₂），如何求A、B两点间的的距离|AB|的值？

过点A向y轴作垂线AN₁、过点B向x轴作垂线BM₂ ，垂足分别为N₁（0，y₁）和M₂（x₂ ， 0），直线AN₁和BM₂相交于点Q．

在Rt△AQB.|AB|²= |AQ|²+ |BQ|²

为了计算AQ和BQ，过点A向x轴作垂线，垂足为M₁（x₁ ， 0）；过点B向y轴作垂线，垂足为N₂（0，y₂），于是有|AQ|=|M₁M₂|=|x₃-x₁|，|BQ|=|N₁N₂|=|y₂-y₁|．

所以，|AB|²= $\text{[math]}$ ．

由此得到A（x₁ ， y₁）、B（x₂ ， y₂）两点间的距离公式： $\text{[math]}$ ．

根据定义：两点之间线段的长度，叫做这两点之间的距离．

因此，线段AB的长度计算公式为 $\text{[math]}$ ．
1. （1）（问题）
  平面直角坐标系中有两点A（0，1）、B（2，3），求线段AB的长；
2. （2） $\text{[math]}$ 表示线段MN的长，其中点M的坐标为（a，b），点N的坐标为；
3. （3）如图，在x轴上有一点P（x，0），试求PA+PB的最小值．
答案解析收藏纠错 + 选题

三、勾股树（数）问题

11. (2024八下·宁明期末) 若3、4、a为勾股数，则a的值为（）

A . $\text{[math]}$ B . 5 C . 5或7 D . 5或 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2021八下·南宁期中) 如图是一棵勾股数，它是由正方形和直角三角形拼成的，若正方形 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的面积分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，则最大正方形 $\text{[math]}$ 的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2019八上·新兴期中) 若3，4，a和5，b，13是两组勾股数，则a+b的值是。

答案解析收藏纠错 + 选题
14. (2023八下·滨海期中) 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形.若正方形A，B，C，D的边长分别是3、6、2、3，则最大正方形 $\text{[math]}$ 的面积是（）

A . 14 B . 34 C . 58 D . 72

答案解析收藏纠错 + 选题
15. (2023九下·柯桥月考) 汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”.如图，大正方形 $\text{[math]}$ 由四个全等的直角三角形和一个小正方形组成，若 $\text{[math]}$ ， $\text{[math]}$ 的面积为3，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

四、以直角三角形三边为边为边长的面积问题

16. (2023八下·广州期末) 如图，在直线l上有正方形a，b，c，若a，c的面积分别为4和16，则b的面积为（）

A . 24 B . 20 C . 12 D . 22

答案解析收藏纠错 + 选题
17. (2023八下·青秀月考) 如图所示的图形表示勾股定理的一种证明方法，该方法运用了祖冲之的出入相补原理.若图中空白部分的面积是 $\text{[math]}$ ，整个图形 $\text{[math]}$ 连同空白部分 $\text{[math]}$ 的面积是 $\text{[math]}$ ，则大正方形 $\text{[math]}$ 的边长是.

答案解析收藏纠错 + 选题
18. (2022八上·南城期中) 我们发现，用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法，请你用等面积法来探究下列两个问题：
1. （1）如图 $\text{[math]}$ 是著名的“赵爽弦图”，由四个全等的直角三角形拼成，请用它验证勾股定理 $\text{[math]}$
2. （2）如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的高， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长度 $\text{[math]}$
3. （3）如图①，若大正方形的面积是 $\text{[math]}$ ，小正方形的面积是 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
19. (2022·瓯海模拟) 如图来自清朝数学家梅文鼎的《勾股举隅》，该图由四个全等的直角三角形围成，延长BC分别交AG，HG于点M，N，梅文鼎就是利用这幅图证明了勾股定理．若图中记△MNG的面积为S，△GDF的面积为9S，则阴影部分的面积为（）

A . 20S B . 21S C . 22S D . 24S

答案解析收藏纠错 + 选题
20. (2022八下·东光期中) 如图是一株美丽的“勾股树”，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的面积分别为5，9，3，5，则最大的正方形 $\text{[math]}$ 的面积是（）

A . 19 B . 22 C . $\text{[math]}$ D . 26

答案解析收藏纠错 + 选题

五、勾股定理与网格问题

21. (2023八下·杭州期中) 作图：
1. （1）直接写出AC的长为 .
2. （2）在图1中找到格点D，画出以点A、B、C、D为顶点的平行四边形，画出所有的情况的平行四边形.
3. （3）在图2中找到格点D，画出以点A、B、C、D为顶点且周长最小的平行四边形，直接写出周长最小值.
4. （4）在（3）条件下，直接写出平行四边形的面积.
答案解析收藏纠错 + 选题
22. (2023八下·安庆期中) 如图，在边长为1个单位长度的小正方形组成的网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画图．
1. （1）在图1中，画一个正方形，使它的面积为10；
2. （2）在图2中，画一个三角形 $\text{[math]}$ ，使它的三边长分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
3. （3）请写出图2中所画 $\text{[math]}$ 的面积为．（直接写出结果）
答案解析收藏纠错 + 选题
23. (2022八上·吉安期末) 如图，已知格点A的坐标为（1，－2），格点B的坐标为（3，2），在4×4的正方形网格中（小正方形的边长为1）取一格点C，构建三边都为无理数的直角三角形ABC，则格点C的坐标可为．

答案解析收藏纠错 + 选题
24. (2021八下·厦门月考) 如图，正方形网格中的每个小正方形边长都是 $\text{[math]}$ ，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形.
1. （1）在图中，画一个三角形，使它们的三边长分别为 $\text{[math]}$ .
2. （2）求 $\text{[math]}$ 边上的高.
答案解析收藏纠错 + 选题
25. (2021·姜堰模拟) 如图，网格中的小正方形边长均为1， $\text{[math]}$ 的三个顶点均在网格的格点上，点D、E分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点， $\text{[math]}$ 与 $\text{[math]}$ 交于O，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为.

答案解析收藏纠错 + 选题

六、勾股定理与折叠问题

26. (2023八下·杭州期中) 如图1，一张矩形纸片ABCD，其中AD＝8cm，AB＝6cm，先沿对角线BD折叠，点C落在点C′的位置，BC′交AD于点G.
1. （1）求证：BG＝DG；
2. （2）求C′G的长；
3. （3）如图2，再折叠一次，使点D与A重合，折痕EN交AD于M，求EM的长.
答案解析收藏纠错 + 选题
27. (2023·博山模拟) 如图，三角形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．沿过点A的直线将纸片折叠，使点B落在边 $\text{[math]}$ 上的点D处；再折叠纸片，使点C与点D重合，若折痕与 $\text{[math]}$ 的交点为E，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
28. (2023八下·龙江月考) 如图，折叠长方形 $\text{[math]}$ 的一边 $\text{[math]}$ ，使点D落在 $\text{[math]}$ 边上的点F处， $\text{[math]}$ ， $\text{[math]}$ ．
求：
1. （1） $\text{[math]}$ 的长；
2. （2） $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
29. (2022八上·龙港期中) 如图，将等边△ABC折叠，使得点C落在AB边上的点D处，EF是折痕，若∠ADE＝90°，AD＝1，则AC的长是（）

A . 2 B . 4 C . 2 $\text{[math]}$ D . 2+ $\text{[math]}$

答案解析收藏纠错 + 选题
30. (2022九上·铁岭月考) 如图，把矩形OABC放入平面直角坐标系中，点B的坐标为（10，8），点D是OC上一点，将△BCD沿边BD折叠，点C恰好落在OA上的点E处，则点D的坐标是（）

A . （0，4） B . （0，5） C . （0，3） D . （0，2）

答案解析收藏纠错 + 选题

七、利用勾股定理求两条线平方和（差）

31. (2023八下·鄱阳月考) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， D是直线 $\text{[math]}$ 上的动点，若 $\text{[math]}$ 是等腰三角形，则 $\text{[math]}$ 的长度是．

答案解析收藏纠错 + 选题
32. (2017·兖州模拟)
如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
1. （1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
2. （2）性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
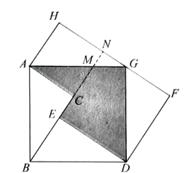
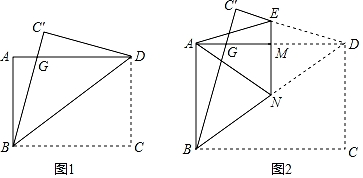
  猜想结论：（要求用文字语言叙
  写出证明过程（先画出图形，写出已知、求证）．
3. （3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5，求GE长．
答案解析收藏纠错 + 选题
33. (2021八上·大邑期中) 在直角三角形ABC中，斜边AB=2，则AB²+AC²+BC²=．

答案解析收藏纠错 + 选题
34. (2020八上·温江月考) 已知Rt△ABC中，∠C＝90°，若a+b＝14cm ， c＝12cm ，则Rt△ABC的面积为．

答案解析收藏纠错 + 选题
35. (2021八上·萧山月考) 如图，已知，直角 $\text{[math]}$ 中， $\text{[math]}$ ，从直角三角形两个锐角顶点所引的中线的长 $\text{[math]}$ ， $\text{[math]}$ ，则斜边 $\text{[math]}$ 之长为．

答案解析收藏纠错 + 选题

八、利用勾股定理证明线段的平方关系

36. (2023·寻乌模拟) 【问题情境】
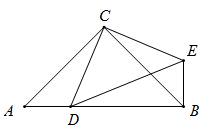
课外兴趣小组活动时，老师提出了如下问题：
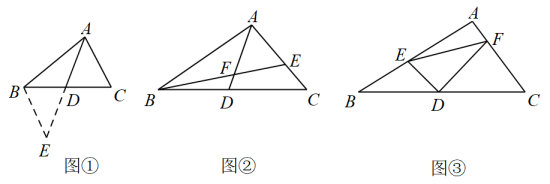
如图①， $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 边上的中线 $\text{[math]}$ 的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．
请根据小明的方法思考：
1. （1）由已知和作图能得到 $\text{[math]}$ ，依据是．
  A． $\text{[math]}$ ；B． $\text{[math]}$ ；C． $\text{[math]}$ ；D． $\text{[math]}$
  由“三角形的三边关系”可求得 $\text{[math]}$ 的取值范围是．
2. （2）【初步运用】
  如图②， $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，交 $\text{[math]}$ 于 $\text{[math]}$ ，且 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
3. （3）【灵活运用】
  如图③，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 中点， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．试猜想线段 $\text{[math]}$ ． $\text{[math]}$ ． $\text{[math]}$ 三者之间的数量关系，并证明你的结论．
答案解析收藏纠错 + 选题
37. (2021九上·科尔沁期末) 在△AED中，EA＝ED，∠AED＝α，点F为直线AD上一动点，连接EF，将线段EF绕点E逆时针旋转α，得到线段EG，连接DG．
1. （1）如图1，探究线段AF、DG之间的数量关系；
2. （2）如图2，当α＝90°时，其它条件不变，试判断线段DF、AF、GF的数量关系，并证明．
答案解析收藏纠错 + 选题
38. (2022八上·余杭月考) 如图，在△ABC和△ECF中，∠ACB=∠ECF=90°，且AC=BC，EC=FC．连接AE，BF交于点O.
1. （1）求证： $\text{[math]}$
2. （2）求∠AOB的度数.
3. （3）连接BE，AF，求证： $\text{[math]}$
答案解析收藏纠错 + 选题
39. (2022八上·代县期末) 综合与实践
美丽的弦图中蕴含着四个全等的直角三角形．
1. （1）如图1，弦图中包含了一大一小两个正方形，已知每个直角三角形较长的直角边为a，较短的直角边为b，斜边长为c，结合图1，试验证勾股定理；
2. （2）如图2，将这四个直角三角形紧密地拼接，形成飞镖状，已知外围轮廓（实线）的周长为24， $\text{[math]}$ ，求该飞镖状图案的面积；
3. （3）如图3，将八个全等的直角三角形紧密地拼接，记图中正方形 $\text{[math]}$ ，正方形 $\text{[math]}$ ，正方形 $\text{[math]}$ 的面积分别为 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
40. (2022八下·佛山月考) 如图，在△ABC中，∠ACB=90°，AC=BC，D是AB边上一点（与A、B不重合），连接CD，将线段CD绕点C按逆时针方向旋转90°得到线段CE，连接DE、BE
1. （1）求证：△ACD≌△BCE；
2. （2）若BE=5，DE=13，求AB的长
答案解析收藏纠错 + 选题