2023年中考数学真题分类汇编（全国版）：二次函数（3）

更新时间：2023-07-27 浏览次数：139 类型：二轮复习

一、选择题

1. 已知 $\text{[math]}$ ，若关于x的方程 $\text{[math]}$ 的解为 $\text{[math]}$ ．关于x的方程 $\text{[math]}$ 的解为 $\text{[math]}$ ．则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九下·薛城模拟) 已知点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，点 $\text{[math]}$ 在抛物线 $\text{[math]}$ 上，若 $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·掇刀期中) 已知抛物线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是常数且 $\text{[math]}$ ）过 $\text{[math]}$ 和 $\text{[math]}$ 两点，且 $\text{[math]}$ ，下列四个结论： $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ 若抛物线过点 $\text{[math]}$ ，则 $\text{[math]}$ ； $\text{[math]}$ 关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有实数根，则其中正确的结论有（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
4. (2023·随州) 如图，已知开口向下的抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ．则下列结论正确的有（）
① $\text{[math]}$ ；

② $\text{[math]}$ ；

③方程 $\text{[math]}$ 的两个根为 $\text{[math]}$ ；

④抛物线上有两点 $\text{[math]}$ 和 $\text{[math]}$ ，若 $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$ ．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2024九下·临渭模拟) 设二次函数 $\text{[math]}$ 是实数 $\text{[math]}$ ，则（）

A . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ B . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ C . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$ D . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最小值为 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·烟台) 如图，抛物线 $\text{[math]}$ 的顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，与 $\text{[math]}$ 轴的一个交点位于0合和1之间，则以下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③若图象经过点 $\text{[math]}$ ，则 $\text{[math]}$ ；④若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 无实数根，则 $\text{[math]}$ ．其中正确结论的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
7. (2023·新疆) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ．结合图象，判断下列结论：①当 $\text{[math]}$ 时， $\text{[math]}$ ；② $\text{[math]}$ 是方程 $\text{[math]}$ 的一个解；③若 $\text{[math]}$ ， $\text{[math]}$ 是抛物线上的两点，则 $\text{[math]}$ ；④对于抛物线， $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是 $\text{[math]}$ ．其中正确结论的个数是（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
8. (2023·枣庄) 二次函数 $\text{[math]}$ 的图象如图所示，对称轴是直线 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ；②方程 $\text{[math]}$ （ $\text{[math]}$ ）必有一个根大于2且小于3；③若 $\text{[math]}$ 是抛物线上的两点，那么 $\text{[math]}$ ；④ $\text{[math]}$ ；⑤对于任意实数m，都有 $\text{[math]}$ ，其中正确结论的个数是（　　）

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题

二、填空题

9. (2023·滨州) 要修一个圆形喷水池，在池中心竖直安装一根水管，水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为 $\text{[math]}$ 处达到最高，高度为 $\text{[math]}$ ，水柱落地处离池中心 $\text{[math]}$ ，水管长度应为．

答案解析收藏纠错 + 选题
10. 已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 两点，若 $\text{[math]}$ 分别位于抛物线对称轴的两侧，且 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
11. (2024九上·新洲月考) 抛物线 $\text{[math]}$ （ $\text{[math]}$ 是常数， $\text{[math]}$ ）经过 $\text{[math]}$ 三点，且 $\text{[math]}$ ．下列四个结论：
① $\text{[math]}$ ；

② $\text{[math]}$ ；

③当 $\text{[math]}$ 时，若点 $\text{[math]}$ 在该抛物线上，则 $\text{[math]}$ ；

④若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个相等的实数根，则 $\text{[math]}$ ．

其中正确的是（填写序号）．

答案解析收藏纠错 + 选题

三、解答题

12. (2023·自贡) 如图，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．
1. （1）求抛物线解析式及 $\text{[math]}$ ， $\text{[math]}$ 两点坐标；
2. （2）以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的四边形是平行四边形，求点 $\text{[math]}$ 坐标；
3. （3）该抛物线对称轴上是否存在点 $\text{[math]}$ ，使得 $\text{[math]}$ ，若存在，求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题

四、综合题

13. (2024·从江模拟) 某校想将新建图书楼的正门设计为一个抛物线型门，并要求所设计的拱门的跨度与拱高之积为 $\text{[math]}$ ，还要兼顾美观、大方，和谐、通畅等因素，设计部门按要求价出了两个设计方案 $\text{[math]}$ 现把这两个方案中的拱门图形放入平面直角坐标系中，如图所示：
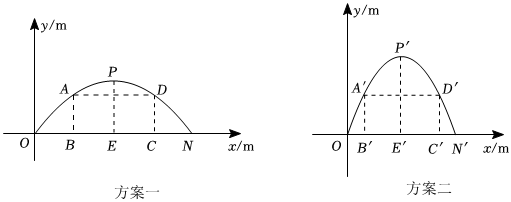
方案一，抛物线型拱门的跨度 $\text{[math]}$ ，拱高 $\text{[math]}$ 其中，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上， $\text{[math]}$ ， $\text{[math]}$ ．

方案二，抛物线型拱门的跨度 $\text{[math]}$ ，拱高 $\text{[math]}$ 其中，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上， $\text{[math]}$ ， $\text{[math]}$ ．

要在拱门中设置高为 $\text{[math]}$ 的矩形框架，其面积越大越好 $\text{[math]}$ 框架的粗细忽略不计 $\text{[math]}$ 方案一中，矩形框架 $\text{[math]}$ 的面积记为 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 在抛物线上，边 $\text{[math]}$ 在 $\text{[math]}$ 上；方案二中，矩形框架 $\text{[math]}$ 的面积记为 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线上，边 $\text{[math]}$ 在 $\text{[math]}$ 上 $\text{[math]}$ 现知，小华已正确求出方案二中，当 $\text{[math]}$ 时， $\text{[math]}$ ，请你根据以上提供的相关信息，解答下列问题：
1. （1）求方案一中抛物线的函数表达式；
2. （2）在方案一中，当 $\text{[math]}$ 时，求矩形框架 $\text{[math]}$ 的面积 $\text{[math]}$ 并比较 $\text{[math]}$ ， $\text{[math]}$ 的大小．
答案解析收藏纠错 + 选题
14. (2024九下·玄武期中) “端午节”吃粽子是中国传统习俗，在“端午节”来临前，某超市购进一种品牌粽子，每盒进价是40元，并规定每盒售价不得少于50元，日销售量不低于350盒，根据以往销售经验发现，当每盒售价定为50元时，日销售量为500盒，每盒售价每提高1元，日销售量减少10盒，设每盒售价为x元，日销售量为p盒．
1. （1）当 $\text{[math]}$ 时， $\text{[math]}$ ；
2. （2）当每盒售价定为多少元时，日销售利润W（元）最大？最大利润是多少？
3. （3）小强说：“当日销售利润最大时，日销售额不是最大，”小红说：“当日销售利润不低于8000元时，每盒售价x的范围为 $\text{[math]}$ ． ”你认为他们的说法正确吗？若正确，请说明理由；若不正确，请直接写出正确的结论．
答案解析收藏纠错 + 选题
15. (2023九下·黄冈模拟) 为了振兴乡村经济，增加村民收入，某村委会干部带领村民在网上直播推销农产品，在试销售的30天中，第x天（ $\text{[math]}$ 且x为整数）的售价p（元/千克）与x的函数关系式 $\text{[math]}$ （且x为整数），销量q（千克）与x的函数关系式为 $\text{[math]}$ ，已知第5天售价为50元/千克，第10天售价为40元/千克，设第x天的销售额为W元
1. （1） $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）求第x天的销售额W元与x之间的函数关系式；
3. （3）在试销售的30天中，销售额超过1000元的共有多少天？
答案解析收藏纠错 + 选题
16. (2023·荆州) 已知：y关于x的函数 $\text{[math]}$ ．
1. （1）若函数的图象与坐标轴有两个公共点，且 $\text{[math]}$ ，则a的值是；
2. （2）如图，若函数的图象为抛物线，与x轴有两个公共点A（-2，0），B（4，0），并与动直线l： $\text{[math]}$ 交于点P，连接PA，PB，PC，BC，其中PA交y轴于点D，交BC于点E．设△PBE的面积为 $\text{[math]}$ ， △CDE的面积为 $\text{[math]}$ ．
  ①当点P为抛物线顶点时，求△PBC的面积；
  
  ②探究直线l在运动过程中， $\text{[math]}$ － $\text{[math]}$ 是否存在最大值？若存在，求出这个最大值；若不存在，说明理由．
答案解析收藏纠错 + 选题
17. (2023·聊城) 如图①，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与y轴交于点C，连接AC，BC.点P是x轴上任意一点．
1. （1）求抛物线的表达式；
2. （2）点Q在抛物线上，若以点A，C，P，Q为顶点，AC为一边的四边形为平行四边形时，求点Q的坐标；
3. （3）如图②，当点 $\text{[math]}$ 从点A出发沿x轴向点B运动时（点P与点A，B不重合），自点P分别作 $\text{[math]}$ ，交AC于点E，作 $\text{[math]}$ ，垂足为点D．当m为何值时， $\text{[math]}$ 面积最大，并求出最大值．
答案解析收藏纠错 + 选题
18. (2024九下·岳阳月考) 已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ， $\text{[math]}$ ，与 $\text{[math]}$ 轴相交于点 $\text{[math]}$ ．
1. （1）求抛物线的表达式；
2. （2）如图1，点 $\text{[math]}$ 是抛物线的对称轴 $\text{[math]}$ 上的一个动点，当 $\text{[math]}$ 的周长最小时，求 $\text{[math]}$ 的值；
3. （3）如图2，取线段 $\text{[math]}$ 的中点 $\text{[math]}$ ，在抛物线上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ ？若存在，求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
19. (2023·滨州) 如图，在平面直角坐标系中，菱形 $\text{[math]}$ 的一边 $\text{[math]}$ 在 $\text{[math]}$ 轴正半轴上，顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 是边 $\text{[math]}$ 上的动点，过点 $\text{[math]}$ 作 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ 交边 $\text{[math]}$ 于点 $\text{[math]}$ ，作 $\text{[math]}$ 交边 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．设 $\text{[math]}$ 的面积为 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式；
2. （2）当 $\text{[math]}$ 取何值时， $\text{[math]}$ 的值最大？请求出最大值．
答案解析收藏纠错 + 选题
20. (2023·邵阳) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 和点 $\text{[math]}$ ，且与直线 $\text{[math]}$ 交于 $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧），点 $\text{[math]}$ 为直线 $\text{[math]}$ 上的一动点，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ．
1. （1）求抛物线的解析式．
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，与拋物线交于点 $\text{[math]}$ ．若 $\text{[math]}$ ，求 $\text{[math]}$ 面积的最大值．
3. （3）抛物线与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为平面直角坐标系上一点，若以 $\text{[math]}$ 为顶点的四边形是菱形，请求出所有满足条件的点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
21. (2023·株洲) 已知二次函数 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，且该二次函数的图象过点 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）如图所示，在平面直角坐标系 $\text{[math]}$ 中，该二次函数的图象与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，点D在 $\text{[math]}$ 上且在第二象限内，点 $\text{[math]}$ 在 $\text{[math]}$ 轴正半轴上，连接 $\text{[math]}$ ，且线段 $\text{[math]}$ 交 $\text{[math]}$ 轴正半轴于点 $\text{[math]}$ ， $\text{[math]}$ ．
  
  ①求证： $\text{[math]}$ ．
  ②当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，且 $\text{[math]}$ ． $\text{[math]}$ 的半径长为线段 $\text{[math]}$ 的长度的 $\text{[math]}$ 倍，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
22. (2024·新疆维吾尔自治区模拟) 如图，二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴的正半轴交于点A，经过点A的直线与该函数图象交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点C．
1. （1）求直线 $\text{[math]}$ 的函数表达式及点C的坐标；
2. （2）点 $\text{[math]}$ 是第一象限内二次函数图象上的一个动点，过点 $\text{[math]}$ 作直线 $\text{[math]}$ 轴于点 $\text{[math]}$ ，与直线 $\text{[math]}$ 交于点D，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ．
  ①当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
  
  ②当点 $\text{[math]}$ 在直线 $\text{[math]}$ 上方时，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴于点 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．设四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式，并求出S的最大值．
答案解析收藏纠错 + 选题
23. (2024·珠海模拟) 如图1，在平面直角坐标系中，已知二次函数 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．
1. （1）求抛物线的解析式；
2. （2）已知 $\text{[math]}$ 为抛物线上一点， $\text{[math]}$ 为抛物线对称轴 $\text{[math]}$ 上一点，以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的三角形是等腰直角三角形，且 $\text{[math]}$ ，求出点 $\text{[math]}$ 的坐标；
3. （3）如图 $\text{[math]}$ ， $\text{[math]}$ 为第一象限内抛物线上一点，连接 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，在点 $\text{[math]}$ 运动过程中， $\text{[math]}$ 是否为定值？若是，求出这个定值；若不是，请说明理由．
答案解析收藏纠错 + 选题
24. (2023·内江) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点．与y轴交于点 $\text{[math]}$ ．
1. （1）求该抛物线的函数表达式；
2. （2）若点P是直线 $\text{[math]}$ 下方抛物线上的一动点，过点P作x轴的平行线交 $\text{[math]}$ 于点K，过点P作y轴的平行线交x轴于点D，求与 $\text{[math]}$ 的最大值及此时点P的坐标；
3. （3）在抛物线的对称轴上是否存在一点M，使得 $\text{[math]}$ 是以 $\text{[math]}$ 为一条直角边的直角三角形：若存在，请求出点M的坐标，若不存在，请说明理由．
答案解析收藏纠错 + 选题
25. (2024·贵池模拟) 已知抛物线 $\text{[math]}$ 交 $\text{[math]}$ 轴于 $\text{[math]}$ 两点， $\text{[math]}$ 为抛物线的顶点， $\text{[math]}$ 为抛物线上不与 $\text{[math]}$ 重合的相异两点，记 $\text{[math]}$ 中点为 $\text{[math]}$ ，直线 $\text{[math]}$ 的交点为 $\text{[math]}$ ．
1. （1）求抛物线的函数表达式；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求证： $\text{[math]}$ 三点共线；
3. （3）小明研究发现：无论 $\text{[math]}$ 在抛物线上如何运动，只要 $\text{[math]}$ 三点共线， $\text{[math]}$ 中必存在面积为定值的三角形．请直接写出其中面积为定值的三角形及其面积，不必说明理由．
答案解析收藏纠错 + 选题
26. 已知抛物线 $\text{[math]}$ 过点 $\text{[math]}$ 和点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．
1. （1）求抛物线的解析式；
2. （2）如图1，连接 $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上（与点 $\text{[math]}$ 不重合），点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，当 $\text{[math]}$ 面积是 $\text{[math]}$ 面积的3倍时，求点 $\text{[math]}$ 的坐标；
3. （3）如图2，点 $\text{[math]}$ 是抛物线上对称轴右侧的点， $\text{[math]}$ 是 $\text{[math]}$ 轴正半轴上的动点，若线段 $\text{[math]}$ 上存在点 $\text{[math]}$ （与点 $\text{[math]}$ 不重合），使得 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
27. (2023·随州) 如图1，平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 过点 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ $\text{[math]}$ 为抛物线上一动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．
1. （1）直接写出抛物线和直线 $\text{[math]}$ 的解析式；
2. （2）如图2，连接 $\text{[math]}$ ，当 $\text{[math]}$ 为等腰三角形时，求 $\text{[math]}$ 的值；
3. （3）当 $\text{[math]}$ 点在运动过程中，在 $\text{[math]}$ 轴上是否存在点 $\text{[math]}$ ，使得以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的三角形与以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为顶点的三角形相似（其中点 $\text{[math]}$ 与点 $\text{[math]}$ 相对应），若存在，直接写出点 $\text{[math]}$ 和点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题