【备考2024年】中考数学杭州卷真题变式分层精准练第22题

更新时间：2023-08-30 浏览次数：65 类型：二轮复习

一、原题

1. (2023·杭州) 设二次函数 $\text{[math]}$ ，（ $\text{[math]}$ ， $\text{[math]}$ 是实数）．已知函数值 $\text{[math]}$ 和自变量 $\text{[math]}$ 的部分对应取值如下表所示：

$\text{[math]}$	…	$\text{[math]}$	0	1	2	3	…
$\text{[math]}$	…	$\text{[math]}$	1	$\text{[math]}$	1	$\text{[math]}$	…

（1）若 $\text{[math]}$ ，求二次函数的表达式；
（2）写出一个符合条件的 $\text{[math]}$ 的取值范围，使得 $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小．
（3）若在m、n、p这三个实数中，只有一个是正数，求 $\text{[math]}$ 的取值范围．

答案解析收藏纠错 + 选题

二、基础

2. (2021九上·崂山期末) 小颖同学想用“描点法”画二次函数y＝ax²+bx+c（a≠0）的图象，取自变量x的6个值，分别计算出对应的y值，如表：
x
……
﹣2
﹣1
0
1
2
3
……
y
……
11
2
﹣1
2
5
m
……
由于粗心，小颖算错了其中的一个y值．
1. （1）求该二次函数表达式；
2. （2）请你指出这个算错的y值；
3. （3）通过计算求m的值．
答案解析收藏纠错 + 选题
3. (2022·和平模拟) 已知二次函数y＝ax²+bx+c（a、b、c是常数，a≠0）的自变量x和函数值y部分对应值如下表：
x
…
0
1
2
3
4
…
y
…
3
0
-1
0
m
…
1. （1）抛物线的对称轴为；
2. （2） m的值为；
3. （3）求该抛物线的解析式；
4. （4）若点A（ $\text{[math]}$ ），B（ $\text{[math]}$ ）都在函数图象上，且 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ （填“>”，“<”或“=”）．
答案解析收藏纠错 + 选题
4. (2023·潮阳模拟) 在平面直角坐标系中，已知点 $\text{[math]}$ ，直线 $\text{[math]}$ 经过点A，抛物线 $\text{[math]}$ 恰好经过A，B，C三点中的两点．
1. （1）求直线 $\text{[math]}$ 的解析式；
2. （2）求a，b的值；
3. （3）平移抛物线 $\text{[math]}$ ，使其顶点仍在直线 $\text{[math]}$ 上，求平移后所得抛物线与y轴交点纵坐标的最大值．
答案解析收藏纠错 + 选题
5. (2022九上·萧山期中) 在平面直角坐标系中，二次函数 $\text{[math]}$ 都是常数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ 和 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的取值范围；
2. （2）已知点 $\text{[math]}$ 在该函数的图象上，且 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标.
答案解析收藏纠错 + 选题
6. (2023九上·鄞州期末) 如图，抛物线 $\text{[math]}$ 与x轴交于A、B两点，与y轴交于C点，点A的坐标为 $\text{[math]}$ ，点C的坐标为 $\text{[math]}$ .
1. （1）求b与c的值；
2. （2）求函数的最大值；
3. （3） $\text{[math]}$ 是抛物线上的任意一点，当 $\text{[math]}$ 时，利用函数图象写出 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
7. (2023·杭州模拟) 设二次函数 $\text{[math]}$ （b，c是常数）的图像与x轴交于A，B两点.
1. （1）若A，B两点的坐标分别为(1，0)，(2，0)，求函数 $\text{[math]}$ 的表达式及其图像的对称轴.
2. （2）若函数 $\text{[math]}$ 的表达式可以写成 $\text{[math]}$ （h是常数）的形式，求 $\text{[math]}$ 的最小值.
3. （3）设一次函数 $\text{[math]}$ （m是常数）.若函数 $\text{[math]}$ 的表达式还可以写成 $\text{[math]}$ 的形式，当函数 $\text{[math]}$ 的图像经过点 $\text{[math]}$ 时，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
8. (2022九上·杭州期中) 已知二次函数 $\text{[math]}$ （m是常数）.
1. （1）若二次函数图象经过 $\text{[math]}$ ，求二次函数的解析式；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ 是该二次函数图象上的两个不同点，求二次函数表达式和n的值；
3. （3）若点 $\text{[math]}$ ，点 $\text{[math]}$ 也均在此函数图象上，且满足 $\text{[math]}$ ，求m的取值范围.
答案解析收藏纠错 + 选题
9. (2022九上·萧山月考) 已知二次函数 $\text{[math]}$ （b为常数）．
1. （1）若图象过 $\text{[math]}$ ，求函数的表达式．
2. （2）在（1）的条件下，当 $\text{[math]}$ 时，求函数的最大值和最小值．
3. （3）若函数图象不经过第三象限，求b的取值范围
答案解析收藏纠错 + 选题
10. (2022九上·福州开学考) 在平面直角坐标系中，设二次函数y₁＝x²+bx+a，y₂＝ax²+bx+1（a，b是实数，a≠0）．
1. （1）若函数y₁的对称轴为直线x＝2，且它的图象经过点（﹣a，b），求函数y₁的解析式．
2. （2）若函数y₂的图象经过点（r，0），其中r≠0，求证：函数y₁的图象经过点（ $\text{[math]}$ ， 0）．
3. （3）设函数y₁和函数y₂的最小值分别为m和n，若m+n＝0，求m，n的值．
答案解析收藏纠错 + 选题

三、提高

11. (2022·鄞州模拟) 如图，已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 、 $\text{[math]}$ 两点.
1. （1）求抛物线的解析式和顶点坐标；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的取值范围；
3. （3）点P为抛物线上一点，若 $\text{[math]}$ ，求出此时点P的坐标.
答案解析收藏纠错 + 选题
12. (2022九上·萧山期末) 已知函数 $\text{[math]}$ （b为常数）.
1. （1）若图象经过点 $\text{[math]}$ ，判断图象经过点 $\text{[math]}$ 吗？请说明理由；
2. （2）设该函数图象的顶点坐标为 $\text{[math]}$ ，当b的值变化时，求m与n的关系式；
3. （3）若该函数图象不经过第三象限，当 $\text{[math]}$ 时，函数的最大值与最小值之差为16，求b的值.
答案解析收藏纠错 + 选题
13. (2023·耿马模拟) 在平面直角坐标系中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在抛物线的对称轴上．
1. （1）若点E在x轴下方的抛物线上，求 $\text{[math]}$ 面积的最大值．
2. （2）抛物线上是否存在一点F，使得以点A，C，D，F为顶点的四边形为平行四边形？若存在，求出点F的坐标，若不存在，请说明理由．
答案解析收藏纠错 + 选题
14. (2023·茂南模拟) 如图，直线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的值和抛物线的解析式．
2. （2） $\text{[math]}$ 为 $\text{[math]}$ 轴上一动点，过点 $\text{[math]}$ 且垂直于 $\text{[math]}$ 轴的直线与直线 $\text{[math]}$ 及抛物线分别交于点 $\text{[math]}$ ．若以 $\text{[math]}$ 为顶点的四边形是平行四边形，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
15. (2022·西城模拟) 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）直接写出c的值和此抛物线的对称轴；
2. （2）若此抛物线与直线 $\text{[math]}$ 没有公共点，求a的取值范围；
3. （3）点 $\text{[math]}$ ， $\text{[math]}$ 在此抛物线上，且当 $\text{[math]}$ 时，都有 $\text{[math]}$ ．直接写出a的取值范围．
答案解析收藏纠错 + 选题
16. (2022九上·龙港期中) 如图，抛物线y＝−x²+bx+c经过点A（-1，0），点B（3，0），与y轴交于点C，点D在射线CO上运动.
1. （1）求该抛物线的表达式和对称轴.
2. （2）过点D作x轴的平行线交抛物线于点E，F（点E在点F的左侧），若EF＝2OC，求点E的坐标.
3. （3）记抛物线的顶点关于直线EF的对称点为点P，当点P到x轴的距离等于1时，求出所有符合条件的线段EF的长.
答案解析收藏纠错 + 选题
17. (2022九上·杭州期中) 设二次函数 $\text{[math]}$ （a，b是常数且 $\text{[math]}$ ）.
1. （1）若函数图象的对称轴为直线 $\text{[math]}$ ，求b的值；
2. （2）若函数图象经过 $\text{[math]}$ 三个点中的两个点，求二次函数的解析式；
3. （3）当 $\text{[math]}$ ，函数图象过两点 $\text{[math]}$ ，当 $\text{[math]}$ 时，总有 $\text{[math]}$ ，求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2022·滨江) 二次函数 $\text{[math]}$ 是常数， $\text{[math]}$ ，当 $\text{[math]}$ 时，函数 $\text{[math]}$ 有最小值 $\text{[math]}$ .
1. （1）若该函数图象的对称轴为直线 $\text{[math]}$ ，并且经过 $\text{[math]}$ 点，求该函数的表达式.
2. （2）若一次函数 $\text{[math]}$ 的图象经过二次函数 $\text{[math]}$ 图象的顶点.
  ①求该二次函数图象的顶点坐标.
  ②若 $\text{[math]}$ 是该二次函数图象上的两点，求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2021九上·河南月考) 已知抛物线y＝ax²+bx+c的顶点为（3，2），且过点（0，11）.
1. （1）求抛物线的解析式；
2. （2）将抛物线先向左平移2个单位长度，再向下平移m（m＞0）个单位长度后得到新抛物线.
  ①若新抛物线与x轴交于A，B两点（点A在点B的左侧），且OB＝3OA，求m的值；
  ②若P（x₁ ， y₁），Q（x₂ ， y₂）是新抛物线上的两点，当n≤x₁≤n+1，x₂≥4时，均有y₁≤y₂ ，求n的取值范围.
答案解析收藏纠错 + 选题

四、培优

20. (2023·邵阳) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 和点 $\text{[math]}$ ，且与直线 $\text{[math]}$ 交于 $\text{[math]}$ 两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧），点 $\text{[math]}$ 为直线 $\text{[math]}$ 上的一动点，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ．
1. （1）求抛物线的解析式．
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的垂线，与拋物线交于点 $\text{[math]}$ ．若 $\text{[math]}$ ，求 $\text{[math]}$ 面积的最大值．
3. （3）抛物线与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为平面直角坐标系上一点，若以 $\text{[math]}$ 为顶点的四边形是菱形，请求出所有满足条件的点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
21. (2023·农安模拟) 在平面直角坐标系中，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 、 $\text{[math]}$ 两点，点P在抛物线上，其横坐标为m ．
1. （1）求此抛物线对应的函数表达式；
2. （2）当点P在y轴右侧且到x轴的距离是4时，求m的值；
3. （3）点Q是抛物线上一点，其横坐标为 $\text{[math]}$ ，抛物线上点P、Q之间的部分图象记为G（包括点P、点Q），当图象G上恰有2个点到直线 $\text{[math]}$ 的距离为1时，直接写出m的取值范围；
4. （4）设点 $\text{[math]}$ ，以 $\text{[math]}$ 为对角线作矩形，矩形的边分别与x轴、y轴平行，当矩形的边与抛物线有两个交点，且最高点与最低点的纵坐标之差为1时，直接写出m的值．
答案解析收藏纠错 + 选题
22. (2023·云梦模拟) 如图1，二次函数 $\text{[math]}$ 的图像与x轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，与y轴交于点C.
1. （1）求二次函数的解析式；
2. （2）点P为抛物线上一动点.
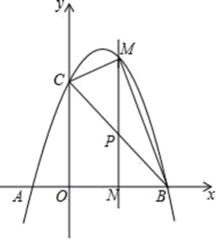
  ①如图2，过点C作x轴的平行线与抛物线交于另一点D，连接 $\text{[math]}$ ， $\text{[math]}$ .当 $\text{[math]}$ 时，求点P的坐标；
  ②如图3，若点P在直线 $\text{[math]}$ 上方的抛物线上，连接 $\text{[math]}$ 与 $\text{[math]}$ 交于点E，求 $\text{[math]}$ 的最大值.
答案解析收藏纠错 + 选题
23. (2022·东营模拟) 如图，已知抛物线y＝ax²+bx+3与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C，连接BC．
1. （1）求抛物线的解析式；
2. （2）若点P为线段BC上的一动点（不与B、C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求点P的坐标；
3. （3）在（2）的条件下，当△BCM的面积最大时，点D是抛物线的对称轴上的动点，在抛物线上是否存在点E，使得以A、P、D、E为顶点的四边形为平行四边形？若存在，请直接写出点E的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
24. (2022·商城模拟) 如图，直线 $\text{[math]}$ 与x轴交于点A（3，0），与y轴交于点B，抛物线 $\text{[math]}$ 经过点A，B.
1. （1）求点B的坐标和抛物线的表达式；
2. （2） P（x₁ ， y₁），Q（4，y₂）两点均在该抛物线上，若y₁≥y₂ ，求P点的横坐标x₁的取值范围；
3. （3）点M为直线AB上一动点，将点M沿与y轴平行的方向平移一个单位长度得到点N，若线段MN与抛物线只有一个公共点，直接写出点M的横坐标的取值范围.
答案解析收藏纠错 + 选题