
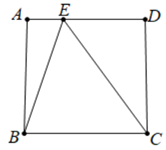
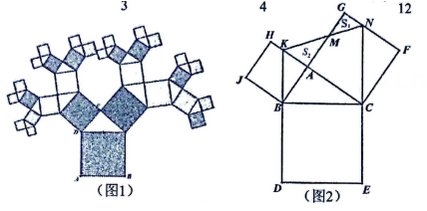



①若 ,
, 求
的长;
②试探究是否为定值.如果是,请求出这个定值;如果不是,请说明理由.


①试判断与
的数量关系和位置关系,并说明理由;
②若 , 求
的值.

①求证:BE=CD,
②猜想∠BDF的度数,并说明理由.


①求证:四边形是菱形;
②连接 , 求
的值.

如图2,平行四边形ABCD,AB=5,BC=4,点E边AB上,点F在边BC的延长线上,连接AF与DE交于点O,当∠FOD=∠B时,求的值;
如图3,菱形ABCD中,(m>2),点E在边AB上,点F是BC延长线上一点,且满足
, 连接AF与DE交于点O时,∠DAO=∠AED;直接写出cos∠ABF的值.(用含m的式子表示)