

 B .
B .  C .
C . 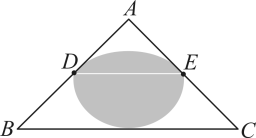 D .
D . 
① ;②若
,则
;③若
,则
;④存在凹四边形
,有
.其中所有正确结论的序号是( )




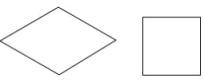
①若菱形的一个内角为 , 则该菱形的“接近度”为;
②当菱形的“接近度”等于时,菱形是正方形.


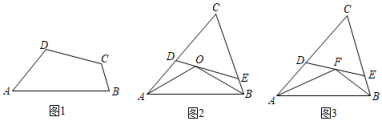

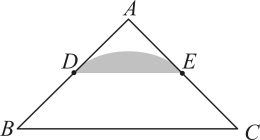
①当∠A=140°时,求∠ADC的度数;
②如图3,当∠A=120°,AB=6时,求阴影部分的面积.
①若 ,则
;
②若 .且
时.则
;
①求证:四边形 是“对补四边形”;
②如图4,连接 ,当
,且
时,求
的值.
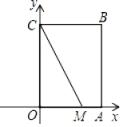
①求BE的长;
②若M、N分别是AB、AD边上的动点,求△MNC周长的最小值.
已知点 ,
.
例如:如图1,已知点 ,
,
在线段
上,则点
是直线
:
轴的“伴随点”.
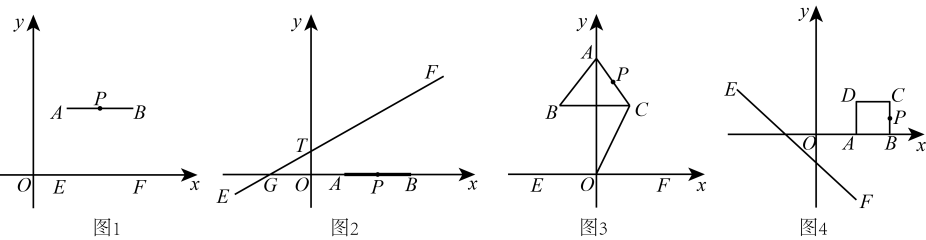

①的中线三角形.(填“是”或“不是”)
②,
,所以
.
如图2,的三条中线分别是
, 将
平移至
, 连接
.
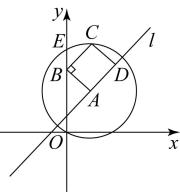
①求的面积的最大值;
②若一次函数图像的“1阶方点”有且只有一个,求a的值;
下面,我们通过折叠的方式折出一个 矩形,如图a所示.
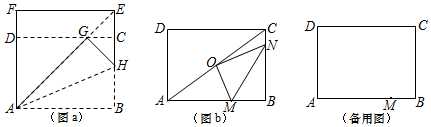
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为 矩形.
①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求 的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2 ,则DR的最小值= ▲ .
定义:将宽与长的比值为(
为正整数)的矩形称为
阶奇妙矩形.
当时,这个矩形为1阶奇妙矩形,如图(1),这就是我们学习过的黄金矩形,它的宽(
)与长
的比值是.
用正方形纸片进行如下操作(如图(2)):
第一步:对折正方形纸片,展开,折痕为 , 连接
;
第二步:折叠纸片使落在
上,点
的对应点为点
, 展开,折痕为
;
第三步:过点折叠纸片,使得点
分别落在边
上,展开,折痕为
.
试说明:矩形是1阶奇妙矩形.
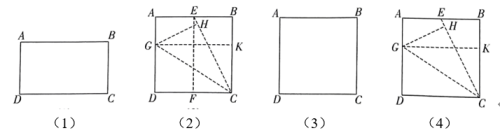
用正方形纸片折叠出一个2阶奇妙矩形.要求:在图(3)中画出折叠示意图并作简要标注.
小明操作发现任一个阶奇妙矩形都可以通过折纸得到.他还发现:如图(4),点
为正方形
边
上(不与端点重合)任意一点,连接
, 继续(2)中操作的第二步、第三步,四边形
的周长与矩形
的周长比值总是定值.请写出这个定值,并说明理由.