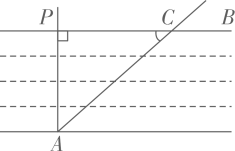



我们所学的锐角三角函数反映了直角三角形中的边角关系:
如图(1)所示.sin α= , cos α=
,
tan α=.
一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得
sin(α+β)=sin αcos β+cos αsin β;sin(α-β)=sin α
cos β-cos αsin β.

例如:sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°
sin 30°=.
任务:
如图2,若将绕点A逆时针旋转一个角度
, 结论“
”仍成立吗?请作出判断,并证明你的结论;
如图3,在(1)的情形下,当点B , D , E三点正好在一条直线上时,求的长.

操作一:如图①,当点与点
重合时,过点
作
, 交
于点
, 连结
, 试判定四边形
的形状,并说明理由;
操作二:如图②,当点落在
边上时,
;
发现:(填“
”或“
”).
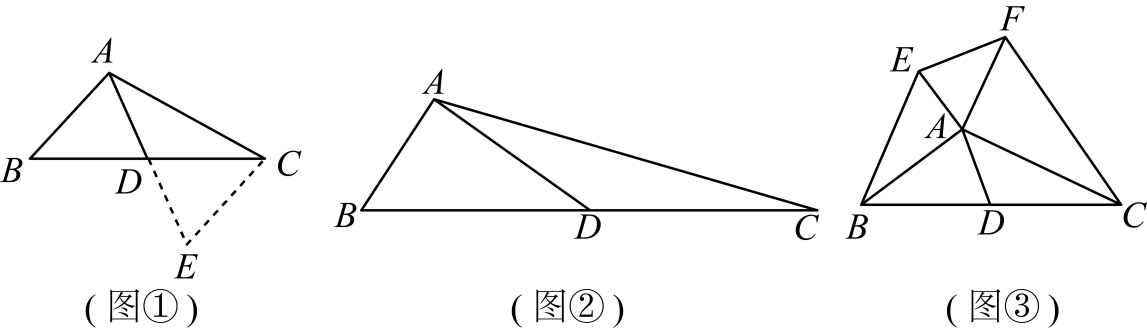
a.如图 , 当点
,
落在对角线
上时,
,
, 则
.
b.如图 , 当点
,
落在对角线
上时,
与
交于点
,
与
交于点
, 连结
, 若
,
,
.
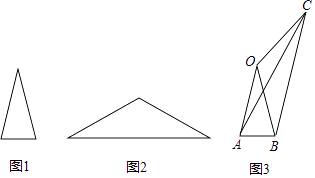
如图1,和
都是等边三角形,连接
. 求证:
.

如图2,和
都是等腰直角三角形,
. 连接
. 请直接写出
的值.
如图3,和
都是直角三角形,
, 且
. 连接
. 延长
交
于点F,交
于点G.求
的值.


【方法尝试】如图1,矩形是矩形
以点A为旋转中心,按逆时针方向旋转
所得的图形,
分别是它们的对角线.求证:
.
【类比迁移】如图2,在和
中,
,
,
,
,
.将
绕点
在平面内逆时针旋转,设旋转角
为
, 连接
,
.
①请判断线段和
的数量关系和位置关系,并说明理由;
②当点B,D,E在同一直线上时,求线段的长.
【拓展延伸】如图3,在中,
,
, 过点
作
, 在射线
上取一点
, 连接
, 使得
, 请直接写出线段
的最值.



| 课题 | 估算仁皇阁高度 |  |
| 测量工具 | 测量角度的仪器,皮尺,刻度尺等 | |
| 组别 | 测量方案示意图 | 测量方案说明 |
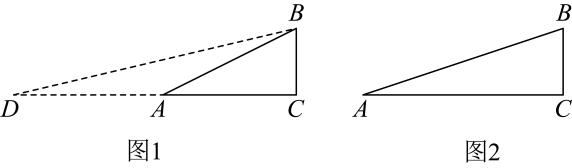
| 组1 |  | 如图1 , 先在仁皇阁底部广场的C处用仪器测得阁楼顶端A的仰角为27° , 然后从C处向阁楼底部前进10m到达D处,此时在D处测得阁楼顶端A的仰角为30° . |
| 组2 | 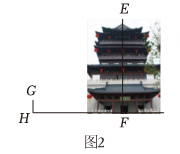 | 如图2 , 身高1.5m的组员站在仁皇阁正门边上合影.打印出照片后量得此组员图上高度GH为0.5cm,量得仁皇阁图上高度EF为12.9cm. |
| 课题 | 检查新生物到皮肤的距离 |
| 工具 | 医疗仪器等 |
| 示意图 |  |
| 说明 | 如图2,新生物在A处,先在皮肤上选择最大限度地避开器官的B处照射新生物,检测射线与皮肤MN的夹角为∠DBN;再在皮肤上选择距离B处9 cm的C处照射新生物,检测射线与皮肤MN的夹角为∠ECN. |
| 测量数据 | ∠DBN=35°,∠ECN=22°,BC=9cm. |
请你根据上表中的测量数据,计算新生物A处到皮肤的距离(结果精确到0.1cm,参考数据:sin35°≈0.57,cos35°≈0.82,tan35≈0.70,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40).

【实践探究】

【问题探究】:
当
平分
时,求
的长;
当
的周长最小时,求
的正切值.
|
课题 |
测量旗杆的高度 |
|
|||
|
成员 |
组长××× 组员:×××,×××,××× |
||||
|
测量工具 |
测量角度的仪器、皮尺等 |
||||
|
测量示意图
|
说明:线段 |
||||
|
|
测量项目 |
第一次 |
第二次 |
平均值 |
|
|
测量数据 |
|
|
|
|
|
|
|
|
|
|
||
|
A,B之间的距离 |
|
|
|
||
任务一:两次测量,A,B之间的距离的平均值是 ▲ m.
任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆的高度.
(参考数据: ,
,
,
,
,
)
任务三:该“综合与实践”小组在制订方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳,你认为其原因可能是什么?
图1是搭成的“倍力桥”,纵梁a,c夹住横梁 |
探究1:
①若有12根横梁绕成环,图4是其侧面示意图,内部形成十二边形 , 求
的值;
②若有根横梁绕成的环(
为偶数,且
, 试用关于
的代数式表示内部形成的多边形
的周长.

如图 , 在▱
中,
,
,
,
是
的中点,点
在
上,且
, 求四边形
的面积;
结果保留根号
如图所示,现规划在一处滩地上规划一个五边形河畔公园
, 按设计要求,要在五边形河畔公园
内挖一个四边形人工湖
, 使点
、
、
、
分别在边
、
、
、
上,且满足
,
已知五边形
中,
,
,
,
,
, 为满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小
请问,是否存在符合设计要求的面积最小的四边形人工湖
?若存在,求四边形
面积的最小值及这时点
到点
的距离;若不存在,请说明理由.