2024年人教版中考数学二轮复习专题17 正方形

更新时间：2024-04-17 浏览次数：25 类型：二轮复习

一、单选题

1. (2023九上·哈尔滨期中) 如图，点 $\text{[math]}$ 在正方形ABCD的边CD上，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 到 $\text{[math]}$ 的位置，连接EF，过点 $\text{[math]}$ 作EF的垂线，垂足为点 $\text{[math]}$ ，与BC交于点 $\text{[math]}$ .若 $\text{[math]}$ ，则CE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·耿马期末) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，交对角线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·苏州模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿线段 $\text{[math]}$ 以1单位长度/秒的速度运动，当点 $\text{[math]}$ 与点 $\text{[math]}$ 重合时，整个运动停止.以 $\text{[math]}$ 为一边向上作正方形 $\text{[math]}$ ，若设运动时间为 $\text{[math]}$ 秒 $\text{[math]}$ ，正方形 $\text{[math]}$ 与 $\text{[math]}$ 重合部分的面积为 $\text{[math]}$ ，则下列能大致反映 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系的图像是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023八下·东阳期末) 延时课上，王林用四根长度都为4cm的木条制作了图1所示正方形，而后将正方形的BC边固定，平推成图2的图形，并测得∠B＝60°，则在此变化过程中结论错误的是（　　）

A . AB长度不变，为4cm B . AC长度变小，减少4 $\text{[math]}$ C . BD长度变大，增大4 $\text{[math]}$ D . ABCD面积变小，减少 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·惠阳期末) 如图，E、F分别是正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上的点，且 $\text{[math]}$ ， $\text{[math]}$ 相交于点O，下列结论： ① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，其中正确的有（）

A . ①②③ B . ②③④ C . ①③④ D . ①②④

答案解析收藏纠错 + 选题
6. (2023·宁波模拟) 如图，在正方形 $\text{[math]}$ 中，P为对角线 $\text{[math]}$ 上一动点， $\text{[math]}$ ， $\text{[math]}$ ，若要知道阴影部分 $\text{[math]}$ 的面积，则只需要知道下列哪个条件（）

A . PB的长 B . PD的长 C . 矩形 $\text{[math]}$ 的面积 D . 矩形 $\text{[math]}$ 对角线的长

答案解析收藏纠错 + 选题
7. (2023·天河模拟) 如图，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 在 $\text{[math]}$ 边上，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，若正方形的边长为4，则 $\text{[math]}$ 的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·达川月考) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点E在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 所在直线翻折得到 $\text{[math]}$ ，延长 $\text{[math]}$ 交边 $\text{[math]}$ 于点G ，连接 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ．其中正确结论的个数是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
9. (2023·宜城模拟) 七巧板是一种古老的中国传统智力玩具，如图，在正方形纸板ABCD中，BD为对角线，E，F分别为BC，CD的中点， $\text{[math]}$ 分别交BD，EF于O，P两点，M，N分别为BO，DO的中点，连接MP，NF，沿图中实线剪开即可得到一副七巧板，则在剪开之前，关于该图形的下列说法：①图中的三角形都是等腰直角三角形；②图中的四边形MPEB是菱形；③四边形EFNB的面积占正方形ABCD面积的 $\text{[math]}$ ．正确的有（）

A . ①③ B . ①② C . 只有① D . ②③

答案解析收藏纠错 + 选题
10. (2023八下·锡山期中) 如图，在边长为1的正方形 $\text{[math]}$ 中，P是对角线 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，过点P作 $\text{[math]}$ ，交 $\text{[math]}$ 于点E，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ 的最小值为 $\text{[math]}$ ，其中正确的是（）．

A . ①② B . ①④ C . ①②③ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题

11. 如图，P是线段AB的黄金分割点，且AP>BP．设以AP为一边的正方形的面积为S₁ ，以BP和AB为边的矩形的面积为S₂ ，比较S₁与S₂的大小：

答案解析收藏纠错 + 选题
12. (2023八下·泸县月考) 如图，矩形内三个相邻的正方形面积分别为4，3和2，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
13. 如图，正方形ABCD的顶点分别在反比例函数y= $\text{[math]}$ (k₁>0)和y= $\text{[math]}$ (k₂>0)的图象上．若BD∥y轴，点D的横坐标为3，则k₁+k₂= ．

答案解析收藏纠错 + 选题
14. (2023九下·杭州月考) 如图，在正方形 $\text{[math]}$ 中，点E，F分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 分别交于点M，N.
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）设 $\text{[math]}$ 和 $\text{[math]}$ 的面积分别为 $\text{[math]}$ 和 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的.
答案解析收藏纠错 + 选题
15. (2023九上·宿城期末) 在平面直角坐标系中，已知点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ ，动点D从A点出发，以每秒1个单位的速度水平向右运动，动点E从点B出发，以每秒1个单位的速度竖直向上运动，过点A作 $\text{[math]}$ 交 $\text{[math]}$ 于点G，当线段 $\text{[math]}$ 的值最小时，则运动时间t的值为 .

答案解析收藏纠错 + 选题
16. (2023·余杭模拟) 如图，已知正方形ABCD的边长为1，点M是BC边上的动点（不与B，C重合），点N是AM的中点，过点N作EF⊥AM，分别交AB，BD，CD于点E，K，F，设BM＝x．
1. （1） AE的长为（用含x的代数式表示）；
2. （2）设EK＝2KF，则 $\text{[math]}$ 的值为．
答案解析收藏纠错 + 选题

三、解答题

17. (2023九上·滕州开学考) 已知：如图，边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别为 $\text{[math]}$ 、 $\text{[math]}$ 上的点，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2） M、 $\text{[math]}$ 分别在 $\text{[math]}$ 、 $\text{[math]}$ 延长线上， $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 与正方形 $\text{[math]}$ 重合部分的面积等于 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. 如图，正方形ABCD 的对角线AC，BD相交于点O，E是OC 上一点，OE=2，连结 EB.过点 A 作AM⊥BE，垂足为 M，AM 与BD 相交于点 F.求OF 的长.

答案解析收藏纠错 + 选题
19. 如图，P，Q分别是边长为1 cm的正方形ABCD的边BC和对角线AC上的两个动点，点P从点B出发，沿BC方向运动，速度为1 cm/s；点Q从点A出发，沿AC方向运动，速度为 $\text{[math]}$ cm/s．只要有一点运动到点C，两点就停止运动．设运动的时间为x(s)，△APQ的面积为y(cm²)．
1. （1）求y关于x的函数表达式及自变量x的取值范围．
2. （2）在运动过程中，能否使△APQ的面积为正方形ABCD的面积的 $\text{[math]}$ ？若能，求出相应x的值；若不能，请说明理由。
答案解析收藏纠错 + 选题
20. (2023八下·安庆期末) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 是对角线 $\text{[math]}$ 上的两点，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）试判断四边形 $\text{[math]}$ 的形状，并加以证明；
3. （3）设 $\text{[math]}$ 的延长线交 $\text{[math]}$ 边于点 $\text{[math]}$ ，若点 $\text{[math]}$ 恰为 $\text{[math]}$ 边的中点，求四边形 $\text{[math]}$ 的周长与面积．
答案解析收藏纠错 + 选题

四、实践探究题

21. (2023九上·平遥月考)
已知四边形ABCD和AEFG均为正方形．
图1 图2
1. （1）观察猜想：如图1所示，当点A、B、G三点在一条直线上时，连接BE、DG ，则线段BE与DG的数量关系是，位置关系是．
2. （2）类比探究：如图2所示，将正方形AEFG在平面内绕点A逆时针旋转到图2时，则（1）的结论是否成立，若成立，请证明，若不成立，请说明理由；
3. （3）拓展延伸：在（2）的条件下，将正方形AEFG在平面内绕点A任意旋转，若AE＝2，AB＝5，则BE的最大值和最小值分别是多少．
答案解析收藏纠错 + 选题
22. (2023九上·安岳期末) 【情境再现】
1. （1）如图1，在正方形 $\text{[math]}$ 中，点E、F分别在边 $\text{[math]}$ 上，且 $\text{[math]}$ ，求证： $\text{[math]}$ .
2. （2）【迁移应用】
  如图2，在矩形 $\text{[math]}$ 中， $\text{[math]}$ （k为常数），点E、F、G、H分别在矩形 $\text{[math]}$ 的边上，且 $\text{[math]}$ ，求证： $\text{[math]}$ .
3. （3）【拓展延伸】
  如图3，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点E、F分别在边 $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
23. (2023八下·铜官期末) 如图，点 $\text{[math]}$ 为正方形 $\text{[math]}$ 内一动点， $\text{[math]}$ ．过点 $\text{[math]}$ 作 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）在（2）的条件下，若点 $\text{[math]}$ 在运动过程中，存在四边形 $\text{[math]}$ 为平行四边形，试探究此时 $\text{[math]}$ 、 $\text{[math]}$ 满足的数量关系．
答案解析收藏纠错 + 选题
24. (2023八下·鄞州期末) 定义：一组邻边相等，另一组邻边也相等的凸四边形叫做“筝形”.如在凸四边形ABCD中，若 $\text{[math]}$ ，则四边形ABCD是“筝形”.
1. （1）【新知学习】
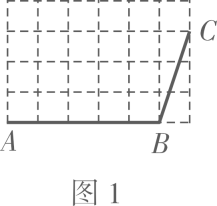
  如图1，在边长为1的正方形网格中，画出“筝形”ABCD，要求点D是格点；
2. （2）【问题探究】
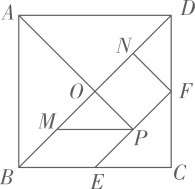
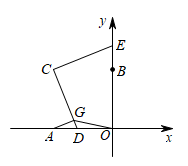
  如图2，在矩形ABCD中， $\text{[math]}$ ， “筝形”EFGH的顶点 $\text{[math]}$ 是AB的中点，点F，G，H分别在BC，CD，AD上，且 $\text{[math]}$ ，求对角线EG的长；
3. （3）【拓展思考】
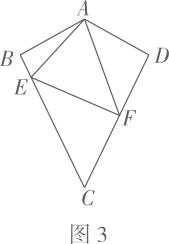
  如图3，在“筝形”ABCD中， $\text{[math]}$ $\text{[math]}$ 分别是BC、CD上的点，AE平分 $\text{[math]}$ ，求“筝形”ABCD的面积.
答案解析收藏纠错 + 选题

五、综合题

25. (2023·宾阳模拟) 综合与探究
问题提出：某兴趣小组在综合与实践活动中提出这样一个问题：在等腰直角三角板 $\text{[math]}$ 中， $\text{[math]}$ ， D为 $\text{[math]}$ 的中点，用两根小木棒构建角，将顶点放置于点D上，得到 $\text{[math]}$ ，将 $\text{[math]}$ 绕点D旋转，射线 $\text{[math]}$ ， $\text{[math]}$ 分别与边 $\text{[math]}$ 交于E，F两点，如图1所示.
1. （1）操作发现：如图2，当E，F分别是 $\text{[math]}$ 的中点时，试猜想线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是；
2. （2）类比探究：如图3，当E，F不是 $\text{[math]}$ 的中点，但满足 $\text{[math]}$ 时，求证 $\text{[math]}$ ；
3. （3）拓展应用：如图4，将两根小木棒构建的角，放置于边长为4的正方形纸板上，顶点和正方形对角线 $\text{[math]}$ 的中点O重合，射线 $\text{[math]}$ 分别与 $\text{[math]}$ 交于E，F两点，且满足 $\text{[math]}$ ，请求出四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
26. (2023八下·通许期末) 如图①，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 是对角线 $\text{[math]}$ 的中点， $\text{[math]}$ 是线段 $\text{[math]}$ 上（不与点 $\text{[math]}$ 重合）的一个动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 交边 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ．
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，如图②，若正方形 $\text{[math]}$ 的边长为2，则点 $\text{[math]}$ 在运动的过程中， $\text{[math]}$ 的长度是否发生变化？若不变，请写出这个不变的值；若变化，请说明理由．
答案解析收藏纠错 + 选题
27. (2023八下·南开期末) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，以 $\text{[math]}$ 、 $\text{[math]}$ 为邻边作矩形 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证：矩形 $\text{[math]}$ 是正方形；
2. （2）求 $\text{[math]}$ 的值；
3. （3）若 $\text{[math]}$ 恰为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，求点 $\text{[math]}$ 到 $\text{[math]}$ 的距离．
答案解析收藏纠错 + 选题
28. (2023八下·灵丘期中) 综合与实跷
通过对《平行四边形》一章内容的学习，我们可以认识到矩形、菱形都是特殊的平行四边形，它们除了具有平行四边形的性质外，还有各自的特殐性质，联系前面学过的三角形知识，我们会发现矩形和菱形中能得到很多特殊的三角形，因此在解决矩形、菱形问题时经常会用到特殊三角形的知识．请你运用所学的知识解答下面的题目．

如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ， D、E两点分别为 $\text{[math]}$ 、 $\text{[math]}$ 两边的中点，过点C作 $\text{[math]}$ 的平行线，与 $\text{[math]}$ 的延长线相交于点F，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）当 $\text{[math]}$ 满足什么条件时，四边形 $\text{[math]}$ 是正方形？请说明理由．
答案解析收藏纠错 + 选题