


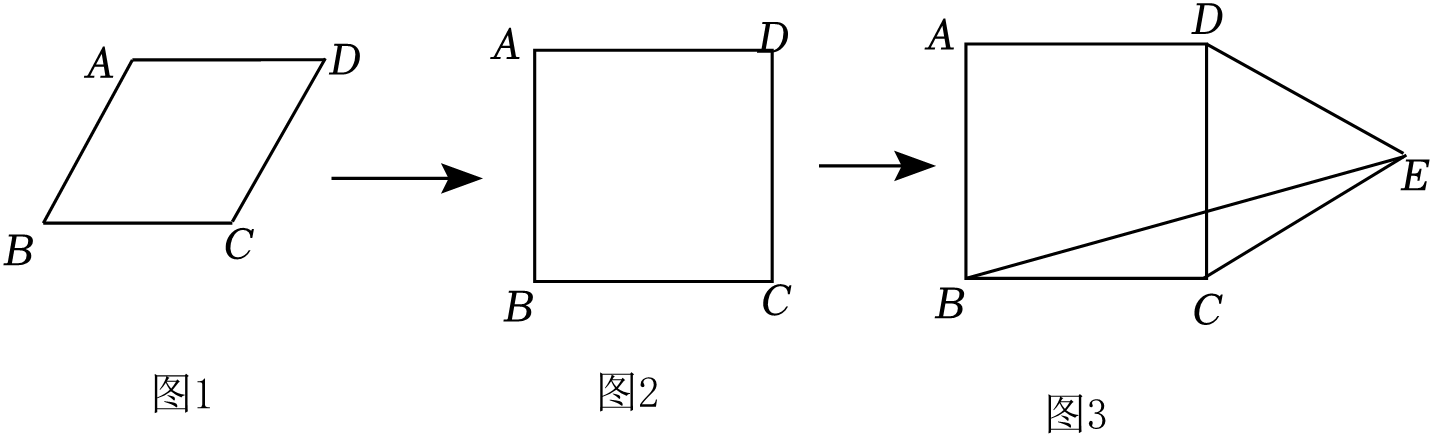


求证:
, 并求
的最小值;
点
在线段
上运动时,点
的横坐标是否发生变化?若不变,请求出点
的横坐标
若变化,请说明理由.
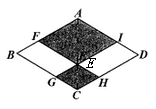
如图1,若点P是边的中点,小南经过探索发现了线段
与
之间的数量关系,请你写出这个关系式.
如图2,小阳说“点P为上任意一点时,(1)中的结论仍然成立”,你同意吗?请说明理由.
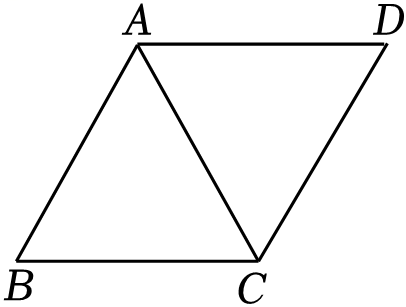
小宛取出如图3所示的菱形纸片 , 测得
,
, 在
边上取一点P,连接
, 在菱形内部作
,
交
于点Q,当
时,请直接写出线段
的长.