B .
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B . 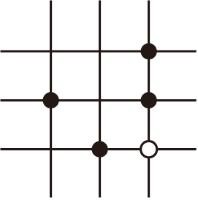 C .
C . 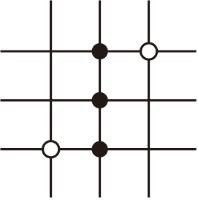 D .
D . 




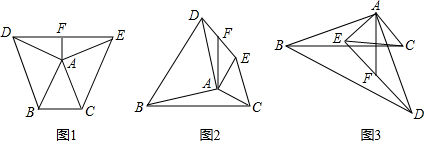
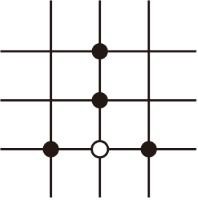
在等腰△ABC中,AB=AC , 分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图①所示,连接DE , 其中F是DE的中点,连接AF , 则下列结论正确的是(填序号即可)
①AF=BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
在任意△ABC中,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图②所示,连接DE , 其中F是DE的中点,连接AF , 则AF和BC有怎样的数量和位置关系?请给出证明过程
在任意△ABC中,仍分别以AB和AC为腰,向△ABC的内侧作等腰直角三角形,如图③所示,连接DE , 其中F是DE的中点,连接AF , 试判断AF和BC的数量和位置关系是否发生改变?并说明理由.
①求证:四边形是平行四边形;
②连接交
于点
, 求
的面积;





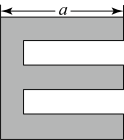
第一步 在矩形纸片一端,利用图的方法折出一个正方形,然后把纸片展平.
第二步 如图 , 把这个正方形折成两个相等的矩形,再把纸片展平.
第三步 如图 , 折出内侧矩形的对角线
, 并把
折到图中所示的
处.
第四步 展平纸片,按所得的点折出
, 使
, 则图④中就出现黄金矩形.
问题解决:

①图中
(保留根号);
②请写出图中所有的黄金矩形:
, 并证明;
③请结合图 , 在矩形
中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并证明.
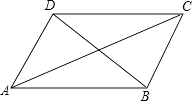
如图所示,在菱形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,且AF=CE,连接BD,DF.求证:四边形BFDE是矩形 |
|
嘉嘉和琪琪分别给出了自己的思路:
嘉嘉:先证明四边形BFDE是平行四边形,然后利用矩形定义即可 得证; 琪琪:先证明△ADF与△CBE全等,然后利用“有三个角是直角的四边形是矩形”即可得证 |
小李同学在用作图软件探索图形性质的数学活动中,进行如下操作:
如图,在边长为3的正方形ABCD的AB边上取定点E , 使AE=1,在AD边上设置动点P , 连接PE , 以PE为边在AB的上方作正方形PEFG , 接AF , BF .

折纸是一种艺术,其中也包含了高超的技术,数学折纸活动有益于开发智力,拓展思维,在折纸活动中体会数学知识的内涵,理解数学知识的应用,可以让我们感悟到严谨的数学之美,八(4)班数学兴趣小组的同学们在活动课进行了折纸问题探究.

【方法提示】
数学折纸问题的解决通常结合轴对称和全等的相关知识性质,要关注折叠前后对应的边和对应的角等一些不变的关系.
【动手操作】
如图,将一张矩形纸片沿长边进行折叠(已知
),使点
落在
边上,折痕为
(点
在
边上,点
在
边上),折叠后点
,
的对应点分别为点
,
.
【问题探究】
其中两个角顶点重合于点
,
与
重合,已知
长
, 请你帮小都同学求出此时点
、
之间的距离;
位置 | 视力值 | |
第1行 | 0.1 | 70 |
第5行 | 0.25 | 28 |
第8行 | 0.5 | 14 |
第14行 | 2.0 | 3.5 |

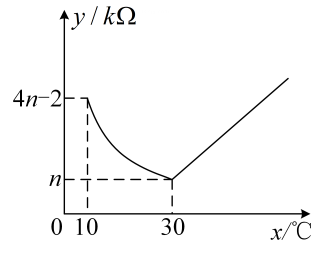
①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式.
②当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时间段学生不能停留在教室里?