
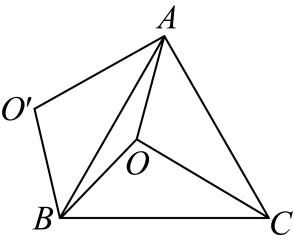
①△DOC是等边三角形;②△BOE是等腰三角形;③BC=AB;④∠AOE=135°;⑤S△AOE=S△BOE .





如图①等边内有一点P , 若点P到顶点A、B、C的距离分别为3,4,5,求
的度数.
解决本题,我们可以将绕顶点A旋转到
处,此时
, 连接
,
是三角形;这样利用旋转变换,我们将三条线段PA、PB、PC转化到一个三角形中,从而求出
°;
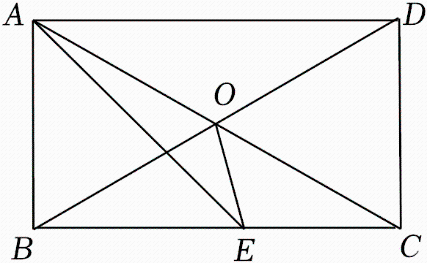
已知如图②,中,
,
, E、F为BC上的点且
, 求证:
;
如图③,在中,
,
,
, 点O为
内一点,连接AO , BO , CO , 且
, 求出
的值.
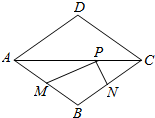
①尺规作图:连接CD , 在CD右侧作等边 , 直线DE与直线CB交于点F . (不写作法,保留作图痕迹)
②连接BE , 在①的条件下,求证: .

②若BE=4DE , 直接写出△CQE与△CMF的面积比 .


①设 ,
, 请用关于x的代数式表示y;
②若 , 求EG的长.
阅读1:a、b为实数,且a>0,b>0,因为 , 所以
从而
(当a=b时取等号).
阅读2:若函数;(m>0,x>0,m为常数),由阅读1结论可知:
, 所以当
, 即
时,函数
的最小值为
.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 , 周长为2(
),求当x= 时,周长的最小值为 ;
问题2:已知函数(
)与函数
(
),
当x= 时,的最小值为 ;
问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
求证:;
例:将分式表示成部分分式,解:设
, 将等式右边通分,得
, 依据题意,得
, 解得
, 所以
请你适用上面所学到的方法,解决下面的问题: