 B .
B .  C .
C .  D .
D . 
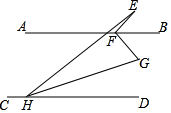


①当射线PN平分∠EPF时,求∠AEM的度数;
②当直线EM与直线PN平行时,求t的值.
如图,点O在直线AB上,OC、OD在直线AB上方,且 , 射线OE是
的“好线”.

经过组内合作交流,小明得到了如下的解决方法:延长到点E , 使
.请根据小明的方法思考:

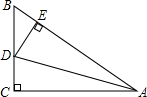
如图2,已知 ,
,
, P为
的中点.若A , C , D共线,求证:
平分
;
【问题背景】
小亮想测量他家门口水塘两个端点A , B长度(如图1),但是小亮找不足够长度的的绳子,小亮寻求哥哥的帮助.
【理论准备】
哥哥帮他出了这样一个方法:先在地上取一个可以直接到达A点和B点的点C , 连接并延长到D , 使
;连接
并延长到E , 使
, 连接
并测量出它的长度(如图2),请你帮小亮说明
的长度等于水塘两个端点
长度的原因;

【实际操作】
小亮实际测量时发现但是由于房屋的阻挡,无法采用上述的方法进行测量,哥哥提出仍然可以计算出长度(如图3),方法如下:
⑴在房屋M墙边找一点C , 使得
;
⑵在院子里找一点E , 使得:此时发现
;
⑶测量出B到房屋M墙的距离
, 即:
,
;
⑷测量出A到的距离
, 即:AE⊥CE ,
, 同时发现
;
经过以上的方法可以计算出的长度.
请根据哥哥的思路提示,帮助小亮完成计算出的长度:
解:如图4,延长至F , 使得
, 连接
.
……

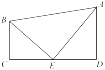
如图5,海警船甲在指挥中心(A处)北偏西的B处,一艘可疑船只乙在指挥中心正东方向的C处,并且两艘船到指挥中心A的距离相等(
),可疑船只沿北偏东
的方向以20海里/小时的速度行驶,指挥中心命令海警船甲从B点向正东方向以30海里/小时的速度追击,两船前进3小时后,指挥中心观测到甲、乙两船分别到达D , E处,且两船和指挥中心形成的夹角为
, (
),请直接写出此时甲、乙两船之间的距离
.



①请你仿照以上过程,在下图中画出一条直线b,使直线b经过点P,且b∥a,要求保留折纸痕迹,画出所用到的直线,无需写画法.
②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的 ▲ 线.


求证:BE∥CF.
要求:请你阅读小宁同学如下的证明过程,圈出他证明中的不符合题意,并在右侧的空白处进行改正,若有跳步,请在下面方框内补充完整并将其标记到证明过程中的相应位置,可如下所示使用修改替换符号:“![]() ”
”
证明:∵AB∥CD ![]()
∴∠ABC=∠BCD(同位角相等,两直线平行).两直线平行,内错角相等.
∵BE平分∠ABC,CE平分∠BCD(已知),
∴∠2=∠3(角平分线的定义).
∴BE∥CF(两直线平行,内错角相等)
