【培优版】浙教版数学九上4.4 两个三角形相似的判定同步练...

更新时间：2024-09-27 浏览次数：6 类型：同步测试

一、选择题

1. (2024九下·哈尔滨开学考) 如图，点 $\text{[math]}$ 是□ABCD的边BA延长线上一点，连接CE，交边AD于点F，则下列各式正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·叙州模拟) 如图， $\text{[math]}$ 的顶点 $\text{[math]}$ 在第一象限内，边 $\text{[math]}$ 在 $\text{[math]}$ 轴正半轴上，点 $\text{[math]}$ 为原点，反比例函数 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，且点 $\text{[math]}$ 为 $\text{[math]}$ 中点， $\text{[math]}$ ，若 $\text{[math]}$ 的面积为14，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·广州月考) 如图，一块矩形木板 $\text{[math]}$ ，长 $\text{[math]}$ ，宽 $\text{[math]}$ ，小虎将一块等腰直角三角板的一条直角边靠在顶点 $\text{[math]}$ 上，另一条直角边与 $\text{[math]}$ 边交于点 $\text{[math]}$ ，三角板的直角顶点 $\text{[math]}$ 在 $\text{[math]}$ 边上移动（不含端点 $\text{[math]}$ ），当线段 $\text{[math]}$ 最短时， $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·桥西期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边一点且 $\text{[math]}$ ，若过点 $\text{[math]}$ 作直线截 $\text{[math]}$ ，使截得的三角形与原三角形相似，则满足条件的直线有（）

A . $\text{[math]}$ 条 B . $\text{[math]}$ 条 C . $\text{[math]}$ 条 D . $\text{[math]}$ 条

答案解析收藏纠错 + 选题
5. (2024九上·深圳期末) 如图，在矩形 $\text{[math]}$ 中，以A为圆心， $\text{[math]}$ 长为半径画圆弧，交 $\text{[math]}$ 于点E ，以E为圆心 $\text{[math]}$ 长为半径画圆弧与 $\text{[math]}$ 的延长线交于点F ，连接 $\text{[math]}$ 分别与 $\text{[math]}$ 、 $\text{[math]}$ 交于点M、N ，连接 $\text{[math]}$ ，下列结论中下列结论中错误的是（）

A . 四边形 $\text{[math]}$ 为菱形 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·杭州模拟) 如图，在△ABC中，点D是AB上一点(不与点A ， B重合)，过点D作DE∥BC交AC于点E ，过点E作EF//AB交BC于点F ，点G是线段DE上一点，EG=2DG ，点H是线段CF上一点，CH=2HF ，连接AG ， AH ， GH ， HE. 若已知△AGH的面积，则一定能求出（）

A . △ABC的面积 B . △ADE的面积 C . 四边形DBFE的面积 D . △EFC的面积

答案解析收藏纠错 + 选题
7. (2024·金华模拟) 如图，四个全等的直角三角形排成“赵爽弦图”，其中四边形ABCD与四边形EFGH都是正方形.连结DG并延长，交BC于点 $\text{[math]}$ ，点 $\text{[math]}$ 为BC的中点.若 $\text{[math]}$ ，则AE的长为（）

A . 4 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·鄞州月考) 如图，在△ABC $\text{[math]}$ 纸板中，AC=4，BC=8，AB=10，P是BC上一点，沿过点P $\text{[math]}$ 的直线剪下一个与△ABC相似的小三角形纸板．针对CP $\text{[math]}$ 的不同取值，三人的说法如下．下列判断正确的是（）
甲：若CP=4， $\text{[math]}$ 则有3 $\text{[math]}$ 种不同的剪法；乙：若CP=2， $\text{[math]}$ 则有4 $\text{[math]}$ 种不同的剪法；
丙：若CP=1， $\text{[math]}$ 则有3 $\text{[math]}$ 种不同的剪法．

A . 只有甲错 B . 只有乙错 C . 只有丙错 D . 甲、乙、丙都对

答案解析收藏纠错 + 选题

二、填空题

9. (2024·安新模拟) 如图，在四边形ABCD中，连接AC ， BD交于点E ，已知BE＝CE ， AB＝AD ， ∠ECB＝2∠ABD ，若BD＝16，AC＝11，则边AB的长为．

答案解析收藏纠错 + 选题
10. (2024九下·深圳期中) 如图所示，点A₁ ， A₂ ， A₃在x轴上且OA₁＝A₁A₂＝A₂A₃ ，分别过点A₁ ， A₂ ， A₃作y轴的平行线与反比例函数y $\text{[math]}$ （k＞0，x＞0）的图象分别交于点B₁ ， B₂ ， B₃ ，分别过点B₁ ， B₂ ， B₃作x轴的平行线分别与y轴交于点C₁ ， C₂ ， C₃ ，连接OB₁ ， OB₂ ， OB₃ ，那么图中阴影部分的面积之和为．

答案解析收藏纠错 + 选题
11. (2024·深圳模拟) 如图，在矩形ABCD中，E是AB的中点，作 $\text{[math]}$ 交BC于点F ，对角线AC分别交DE ， DF于点G ， H ，当DH⊥AC时，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
12. (2024·深圳模拟) 如图，正比例函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于A ， B两点，过点A的直线分别与x轴、y轴交于C ， D两点．当 $\text{[math]}$ ，时，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024·河北) 如图，△ABC的面积为2，AD为BC边上的中线，点A ， C₁ ， C₂ ， C₃是线段CC₄的五等分点，点A ， D₁ ， D₂是线段DD₃的四等分点，点A是线段BB₁的中点．
1. （1） △AC₁D₁的面积为；
2. （2） △B₁C₄D₃的面积为．
答案解析收藏纠错 + 选题

三、解答题

14. (2023九上·义乌月考) 矩形ABCD中，M ， N分别是边AB ， BC上的两个动点.
1. （1）如图，当 DM⊥ MN ， AM=BM时. 求证：①△DAM∽△MBN；②DN=AD+BN.
2. （2）当 AB=5，BC=3 时，是否存在点 M的某个位置，使得△DAM∽△MBN∽△DCN ，
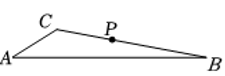
  若存在，求 AM的长. 若不存在，说明理由.
3. （3）是否存在矩形 ABCD ，使得△DAM ， △MBN ， △DCN都和△DMN相似，若存在，求 $\text{[math]}$ 的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题
15. (2024·重庆) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点P为AB上一点， $\text{[math]}$ ，过点P作 $\text{[math]}$ 交AC于点Q点P ， Q的距离为 $\text{[math]}$ ， $\text{[math]}$ 的周长与 $\text{[math]}$ 的周长之比为 $\text{[math]}$ .
1. （1）请直接写出 $\text{[math]}$ ， $\text{[math]}$ 分别关于x的函数表达式，并注明自变量x的取值范围；
2. （2）在给定的平面直角坐标系中，画出函数 $\text{[math]}$ ， $\text{[math]}$ 的图象，并分别写出函数 $\text{[math]}$ ， $\text{[math]}$ 的一条性质；
3. （3）结合函数图象，请直接写出 $\text{[math]}$ 时x的取值范围（近似值保留小数点后一位，误差不超过0.2）.
答案解析收藏纠错 + 选题

四、实践探究题

16. (2024九下·榆树开学考) 【教材呈现】如图是华师版九年级上册数学教材第77页的部分内容．
猜想：如图，在△ABC中，点D、E分别是AB与AC的中点．根据画出的图形，可以猜想：
DE∥BC ，且DE＝ $\text{[math]}$ BC
对此，我们可以用演绎推理给出证明．
1. （1）【定理证明】请根据教材内容，结合图①，写出证明过程．
2. （2）【定理应用】如图②，已知矩形ABCD中，AD＝6，CD＝4，点P在BC上从B向C移动，R、E、F分别是DC、AP、RP的中点，则EF＝．
3. （3）【拓展提升】如图③，△ABC中，AB＝12，BC＝16，点D ， E分别是AB ， AC的中点，点F在DE上，且∠AFB＝90°，则EF＝．
答案解析收藏纠错 + 选题
17. (2023·铜仁模拟) $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为直线 $\text{[math]}$ 上一动点 $\text{[math]}$ 点 $\text{[math]}$ 不与 $\text{[math]}$ ， $\text{[math]}$ 重合 $\text{[math]}$ ，以 $\text{[math]}$ 为边在 $\text{[math]}$ 右侧作菱形 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）观察猜想：如图 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上时，
  $\text{[math]}$ 与 $\text{[math]}$ 的位置关系为：．
  $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系为：；
2. （2）数学思考：如图 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上时，结论 $\text{[math]}$ ， $\text{[math]}$ 是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
3. （3）拓展延伸：如图 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上时，设 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，若已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
18. (2024·台儿庄模拟)
1. （1）如图1，在矩形 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ．求证： $\text{[math]}$ ．
2. （2）【问题解决】
  如图2，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．求证： $\text{[math]}$ ．
3. （3）【类比迁移】
  如图3，在菱形 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题