整式的混合运算—人教版数学八（上）知识点训练

更新时间：2024-11-26 浏览次数：1 类型：复习试卷

一、基础夯实

1. (2024·辽宁) 下列计算正确的是（）

A . a²+a³＝2a⁵ B . a²•a³＝a⁶ C . （a²）³＝a⁵ D . a（a+1）＝a²+a

答案解析收藏纠错 + 选题
2. (2023九下·宁波竞赛) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·岳阳期中) 若（2x﹣y）²+M＝4x²+y² ，则整式M为（　　）

A . ﹣4xy B . 2xy C . ﹣2xy D . 4xy

答案解析收藏纠错 + 选题
4. (2024八上·深圳开学考) 已知2a²﹣a﹣3＝0，则（2a+3）（2a﹣3）+（2a﹣1）²的值是（　　）

A . 6 B . ﹣5 C . ﹣3 D . 4

答案解析收藏纠错 + 选题
5. (2024八上·益阳开学考) 定义三角表示3abc ，方框表示xz＋wy ，则×的结果为( )

A . 72m²n－45mn² B . 72m²n＋45mn² C . 24m²n－15mn² D . 24m²n＋15mn²

答案解析收藏纠错 + 选题
6. (2024七上·宁波期中) 如图，7张全等的小长方形纸片(既不重叠也无空隙)放置于矩形ABCD中，设小长方形的长为a，宽为b(a>b)，若要求出两块黑色阴影部分的周长和，则只要测出下面哪个数据（）

A . a B . b C . a+b D . a-b

答案解析收藏纠错 + 选题
7. (2024七下·海曙期末) 如图，将两张边长分别为 $\text{[math]}$ 和 $\text{[math]}$ 的正方形纸片按图 1，图 2 两种方式放置长方形内 (图 1，图 2 中两张正方形纸片均有部分重叠)，未被这两张正方形纸片覆盖的部分用阴影部分表示. 设图 1 中阴影部分面积为 $\text{[math]}$ ，图 2 中阴影部分面积为 $\text{[math]}$ . 当 $\text{[math]}$ 时， $\text{[math]}$ 的值为 ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 已知 $\text{[math]}$ 则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
9. (2024八上·岳阳开学考) 若方程组 $\text{[math]}$ 的解是 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2024七下·冷水滩期末) 已知 $\text{[math]}$ 与 $\text{[math]}$ 互为相反数，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
11. 先化简，再求值：
1. （1） $\text{[math]}$ 其中 $\text{[math]}$
2. （2） $\text{[math]}$ 其中x= $\text{[math]}$
3. （3） $\text{[math]}$ $\text{[math]}$ 其中x- $\text{[math]}$
答案解析收藏纠错 + 选题
12. (2024八上·天心开学考) 先化简，再求值：已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值，其中 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2024八上·香洲开学考) “以形释数”是利用数形结合思想证明代数问题的一种体现，做整式的乘法运算时利用几何直观的方法获取结论，在解决整式运算问题时经常运用．
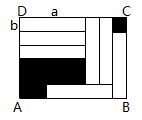
例1：如图1，可得等式： $\text{[math]}$ ；
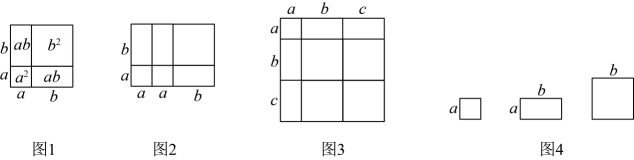
例2：由图2，可得等式： $\text{[math]}$ ．
1. （1）如图3，将几个面积不等的小正方形与小长方形拼成一个边长为 $\text{[math]}$ 的正方形，从中你发现的结论用等式表示为______；
2. （2）利用（1）中所得到的结论，解决下面的问题：已知 $\text{[math]}$ ， $\text{[math]}$ ．求 $\text{[math]}$ 的值．
3. （3）如图4，拼成 $\text{[math]}$ 为大长方形，记长方形 $\text{[math]}$ 的面积与长方形 $\text{[math]}$ 的面积差为S．设 $\text{[math]}$ ，若S的值与 $\text{[math]}$ 无关，求a与b之间的数量关系．
答案解析收藏纠错 + 选题

二、能力提升

14. (2024八上·东阳开学考) 如图，有三张边长分别为a，b，c的正方形纸片A，B，C，将三张纸片按图1，图2两种不同方式放置于同一长方形中．记图1中阴影部分周长为 $\text{[math]}$ ，面积为 $\text{[math]}$ ；图2中阴影部分周长为 $\text{[math]}$ ，面积为 $\text{[math]}$ ，若 $\text{[math]}$ ，则b与c满足的关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2024八上·重庆市期中) 关于x的二次三项式 $\text{[math]}$ （a，b均为非零常数），关于x的三次三项式 $\text{[math]}$ （其中c，d，e，f均为非零常数），下列说法中正确的个数有（）
①当 $\text{[math]}$ 时， $\text{[math]}$ ；
②当 $\text{[math]}$ 为关于x的三次三项式时，则 $\text{[math]}$ ；
③当多项式M与N的乘积中不含 $\text{[math]}$ 项时，则 $\text{[math]}$ ；
④ $\text{[math]}$ ；

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
16. (2024七下·杭州期中) 计算 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2017七下·丰台期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
18. (2024八上·宁江期末) 观察下列等式，回答问题．
$\text{[math]}$ ；
$\text{[math]}$ ；
$\text{[math]}$ ；
$\text{[math]}$ ；
1. （1）试求 $\text{[math]}$ 的值；
2. （2）判断 $\text{[math]}$ 的值的个位数字是几？
答案解析收藏纠错 + 选题
19. (2024八上·斗门期末) 小戴同学通过计算下列两位数的乘积，发现结果也存在一定的规律，请你补充小戴同学的探究过程：
$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
1. （1）利用发现的规律计算 $\text{[math]}$ ．
2. （2）根据发现，若设一个两位数的十位上的数字为 $\text{[math]}$ ，个位上的数字为 $\text{[math]}$ ，则另一个两位数的个位上的数字为；
  用含 $\text{[math]}$ 、 $\text{[math]}$ 的等式表示以上两位数相乘的规律；
3. （3）请用所学知识证明②中的规律．
答案解析收藏纠错 + 选题
20. (2023八上·平城月考) 【阅读材料】“数形结合”是一种非常重要的数学思想方法．比如：在学习“整式的乘法”时，我们通过构造几何图形，用“等积法”直观地推导出了完全平方和公式： $\text{[math]}$ （如图1）．利用“数形结合”的思想方法，可以从代数角度解决图形问题，也可以用图形关系解决代数问题．
【方法应用】根据以上材料提供的方法，完成下列问题：
1. （1）由图2可得等式：；由图3可得等式：；
2. （2）利用图3得到的结论，解决问题：若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；
3. （3）如图4，若用其中 $\text{[math]}$ 张边长为 $\text{[math]}$ 的正方形， $\text{[math]}$ 张边长为 $\text{[math]}$ 的正方形， $\text{[math]}$ 张边长分别为a、b的长方形纸片拼出一个面积为 $\text{[math]}$ 长方形（无空隙、无重叠地拼接），则 $\text{[math]}$ ．
答案解析收藏纠错 + 选题

三、拓展创新

21. (2024七上·西城期中) “铺地锦”是我国明朝《算法统宗》里介绍的一种乘法运算方法，可将多位数乘法运算转化为一位数乘法和简单的加法运算．小明受其启发，设计了如图1所示的“表格算法”，图1表示 $\text{[math]}$ ，运算结果为3266．图2表示一个三位数与一个两位数相乘，表格中部分数据被墨迹覆盖，根据图2中现有数据进行推断，正确的是（）

A . “15”左边的数是12 B . “15”右边的“ $\text{[math]}$ ”表示5 C . 运算结果小于6000 D . 运算结果可以表示为 $\text{[math]}$

答案解析收藏纠错 + 选题
22. (2024八上·江北开学考) 有依次排列的两个整式 $\text{[math]}$ ， $\text{[math]}$ ，用后一个整式 $\text{[math]}$ 与前一个整式 $\text{[math]}$ 作差后得到新的整式记为 $\text{[math]}$ ，用整式 $\text{[math]}$ 与前一个整式 $\text{[math]}$ 作差后得到新的整式 $\text{[math]}$ ，用整式 $\text{[math]}$ 与前一个整式 $\text{[math]}$ 作差后得到新的整式 $\text{[math]}$ ，依次进行作差的操作得到新的整式．下列说法：①当 $\text{[math]}$ 时， $\text{[math]}$ ；②当 $\text{[math]}$ 时， $\text{[math]}$ ；③ $\text{[math]}$ 正确的说法有（）个

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
23. (2024九上·重庆市开学考) 将 $\text{[math]}$ （所有字母均不为0）中的任意两个字母对调位置，称为“对调操作”．例如：“ $\text{[math]}$ 、 $\text{[math]}$ 对调操作”的结果为 $\text{[math]}$ ，且“ $\text{[math]}$ 、 $\text{[math]}$ 对调操作”和“ $\text{[math]}$ 、 $\text{[math]}$ 对调操作”是同一种“对调操作”．
下列说法：
①只有“ $\text{[math]}$ 、 $\text{[math]}$ 对调操作”的结果与原式相等；
②若“ $\text{[math]}$ 、 $\text{[math]}$ 对调操作”与“ $\text{[math]}$ 、 $\text{[math]}$ 对调操作”的结果相等，则 $\text{[math]}$ 或 $\text{[math]}$ ；
③若 $\text{[math]}$ ，则所有的“对调操作”共有5种不同运算结果．
其中正确的个数是（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
24. (2022八上·南昌期中) 阅读材料：
我们定义：如果两个实数的差等于这两个实数的商，那么这两个实数就叫做“差商等数对”．即：如果 $\text{[math]}$ ，那么α与b就叫做“差商等数对”，记为 $\text{[math]}$ ．例如： $\text{[math]}$ ； $\text{[math]}$ ；则称数对 $\text{[math]}$ ， $\text{[math]}$ 是“差商等数对”．
根据上述材料，解决下列问题：
1. （1）下列数对中，“差商等数对”是（填序号）；
  ① $\text{[math]}$ ② $\text{[math]}$ ③ $\text{[math]}$
2. （2）如果 $\text{[math]}$ 是“差商等数对”，请求出a的值；
3. （3）在（2）的条件下，先化简再求值： $\text{[math]}$ ．
答案解析收藏纠错 + 选题