题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

初中数学浙教版八下数学综合题优生特训5

更新时间：2022-06-11 浏览次数：43 类型：复习试卷

一、综合题

1. (2022八下·诸暨期中) 已知，矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
1. （1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
2. （2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
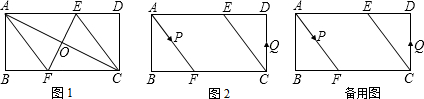
  ①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
  
  ②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．
答案解析收藏纠错 + 选题
2. (2022八下·高青期中) 已知正方形 $\text{[math]}$ ，点F是射线 $\text{[math]}$ 上一动点（不与C，D重合），连接 $\text{[math]}$ 并延长交直线 $\text{[math]}$ 于点E，交 $\text{[math]}$ 于点H，连接 $\text{[math]}$ ，过点C作 $\text{[math]}$ 交 $\text{[math]}$ 于点G．
1. （1）若点F在边 $\text{[math]}$ 上，如图1．
  ①证明： $\text{[math]}$
  ②猜想线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系并说明理由
2. （2）取 $\text{[math]}$ 中点M，连结 $\text{[math]}$ ，若 $\text{[math]}$ ，正方形边长为6，求 $\text{[math]}$ 的长
答案解析收藏纠错 + 选题
3. (2022八下·房山期中) 如图 1，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 为 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ ．点 $\text{[math]}$ 在 $\text{[math]}$ 边上运动．
1. （1）当点 $\text{[math]}$ 和点 $\text{[math]}$ 重合时（如图2），过点 $\text{[math]}$ 做 $\text{[math]}$ 的垂线，垂足为点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ．请直接写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系；
2. （2）当点 $\text{[math]}$ 在 $\text{[math]}$ 边上运动时，过点 $\text{[math]}$ 做 $\text{[math]}$ 的垂线，垂足为点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ （如图 3 ），（1）中的结论依旧成立吗？请证明；
3. （3）如图 4 ，当点 $\text{[math]}$ 在 $\text{[math]}$ 边上运动时， $\text{[math]}$ 为直线 $\text{[math]}$ 上一点，若 $\text{[math]}$ ，请问是否始终能证明 $\text{[math]}$ ？请你说明理由．
答案解析收藏纠错 + 选题
4. (2022八下·大兴期中) 已知四边形ABCD是正方形，点E为射线AC上一动点（点E不与A，C重合），连接DE，过点E作EF⊥DE，交射线BC于点F，过点D，F分别作DE，EF的垂线，两垂线交于点G，连接CG．
1. （1）如图，当点E在对角线AC上时，依题意补全图形，并证明：四边形DEFG是正方形；
2. （2）在（1）的条件下，猜想：CE，CG和AC的数量关系，并加以证明；
3. （3）当点E在对角线AC的延长线上时，直接用等式表示CE，CG和AC的数量关系．
答案解析收藏纠错 + 选题
5. (2022八下·大兴期中) 对于平面直角坐标系xOy中的线段AB和图形M，给出如下的定义：若图形M是以AB．为对角线的平行四边形，则称图形M是线段AB的“关联平行四边形”．点A（8，a），点B（2，b），
1. （1）当a＝8，b＝﹣2时，若四边形AOBC是线段AB的“关联平行四边形”，则点C的坐标是；
2. （2）若四边形AOBC是线段AB的“关联平行四边形”，求对角线OC的最小值；
3. （3）若线段AB的“关联平行四边形”AOBC是正方形，直接写出点C的坐标．
答案解析收藏纠错 + 选题
6. (2022八下·仁寿期中) 如图，在矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是（ $\text{[math]}$ ，8），矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，BD所在直线与OA，x轴分别交于点D，F.
1. （1）求线段BO的长；
2. （2）求直线BD的解析式；
3. （3）点M是直线BD上的一个动点，过点M作MN⊥x轴，垂足为点N.在点M的运动过程中，是否存在以N、E、O为顶点的三角形是等腰三角形？若存在，直接写出点N的坐标并求出点M的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
7. (2022八下·澄城期中) 如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点A作 $\text{[math]}$ 于点E，延长BC至F，使 $\text{[math]}$ .连接DF.
1. （1）求证：四边形ADFE为矩形；
2. （2）连接OF，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求OF的长.
答案解析收藏纠错 + 选题
8. (2022八下·梧州期中) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 取任何实数，方程总有实数根；
2. （2）若直角三角形 $\text{[math]}$ 的一边长为4，另两边m，n的长恰好是这个方程的两个根，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
9. (2022八下·梧州期中) 2019年小王看中了某楼盘以12000元每平方米的均价对外销售面积为100平方米的某户型，由于资金不足，决定等两年再考虑买房.自2019年底出现疫情以来，商品房价格下调，2021年的该户型的均价为9720元每平方米 .
1. （1）求这一户型的均价平均每年下调的百分率；
2. （2）进入2022年后小王得知该户型仍有少量库存在售，单价较2021年的均价再次下调相同的百分率.小王计算了一下自己的资金，在过去的24个月中，每月固定存相相同数量的资金（存入的资金是100的整数倍），加上原有积蓄30万元，还可以向银行贷款50万元，可以凑齐房款，请问小王在过去的两年中每月至少固定存入多少钱？
答案解析收藏纠错 + 选题
10. (2022八下·嵊州期中) 如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点P从点A出发沿边 $\text{[math]}$ 向点C以 $\text{[math]}$ 的速度移动，点Q从C点出发沿 $\text{[math]}$ 边向点B以 $\text{[math]}$ 的速度移动．
1. （1）如果P、Q同时出发，几秒钟后，可使 $\text{[math]}$ 的面积为8平方厘米？
2. （2）点P、Q在移动过程中，是否存在某一时刻，使得 $\text{[math]}$ 的面积等于 $\text{[math]}$ 的面积的一半．若存在，求出运动的时间；若不存在，说明理由.
答案解析收藏纠错 + 选题
11. (2022八下·北仑期中) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒 $\text{[math]}$ 的速度沿折线 $\text{[math]}$ 方向运动，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以每秒 $\text{[math]}$ 的速度沿线段 $\text{[math]}$ 方向向点 $\text{[math]}$ 运动．已知动点 $\text{[math]}$ 、 $\text{[math]}$ 同时出发，当点 $\text{[math]}$ 运动到点 $\text{[math]}$ 时， $\text{[math]}$ 、 $\text{[math]}$ 运动停止，设运动时间为 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的长；
2. （2）当四边形 $\text{[math]}$ 为平行四边形时，求四边形 $\text{[math]}$ 的周长；
3. （3）在点 $\text{[math]}$ 、点 $\text{[math]}$ 的运动过程中，是否存在某一时刻，使得 $\text{[math]}$ 的面积为 $\text{[math]}$ ？若存在，请求出所有满足条件的 $\text{[math]}$ 的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
12. (2022八下·湖州期中) 定义：我们把对角线长度相等的四边形叫做等线四边形．
1. （1）尝试：如图1，在3×3的正方形网格图形中，已知点A、点B是两个格点，请你作出一个等线四边形，要求A、B是其中两个顶点，且另外两个顶点也是格点；
2. （2）推理：如图2，已知△AOD与△BOC均为等腰直角三角形，∠AOD＝∠BOC＝90°，连结AB，CD，求证：四边形ABCD是等线四边形；
3. （3）拓展：如图3，已知四边形ABCD是等线四边形，对角线AC，BD交于点O，若∠AOD＝60°，AB＝ $\text{[math]}$ ，BC＝ $\text{[math]}$ ，AD＝2．求CD的长．
答案解析收藏纠错 + 选题
13. (2022八下·湖州期中) 如图直角坐标系中直线AB与x轴正半轴、y轴正半轴交于A，B两点，已知B（0，4），∠BAO＝30°，P，Q分别是线段OB，AB上的两个动点，P从O出发以每秒3个单位长度的速度向终点B运动，Q从B出发以每秒8个单位长度的速度向终点A运动，两点同时出发，当其中一点到达终点时整个运动结束，设运动时间为t（秒）．
1. （1）求线段AB的长，及点A的坐标；
2. （2） t为何值时，△BPQ的面积为2 $\text{[math]}$ ；
3. （3）若C为OA的中点，连接QC，QP，以QC，QP为邻边作平行四边形PQCD，
  ①t为何值时，点D恰好落在坐标轴上；
  
  ②是否存在时间t使x轴恰好将平行四边形PQCD的面积分成1：3的两部分，若存在，直接写出t的值．
答案解析收藏纠错 + 选题
14. (2022八下·温州期中) 如图1，在Rt△ABC中，∠ACB=90°，∠BAC=30°，BC=3cm，点H为AC边上的一点，且AH=2HC，点P从点A出发以每秒2cm的速度沿AB方向运动，同时点Q从点B出发以每秒1cm速度沿BC方向运动，点Q与点E关于AC对称，以QP、QE为邻边作平行四边形PQEF，当PF经过点H时，PQ同时停止运动，设运动的时间为t秒。
1. （1）求线段PF的长度（用t的代数式表示）．
2. （2）如图2，连接HF、HP，是否存在以HF为腰的等腰△PHF，若存在，求出相应的t的值，若不存在，请说明理由．
3. （3）如图3，连接AF，当PH∥AF时，则PH=．（直接写出答案）
答案解析收藏纠错 + 选题
15. (2022八下·无棣期中) 小明同学在学完第十八章《平行四边形》后，研究了数学教材第64页的数学活动1，其内容如下：如果我们身旁没有量角器或三角尺，有需要做60°，30°，15°等大小的角，可以采用下面的方法（如图1）：
对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；
再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN．
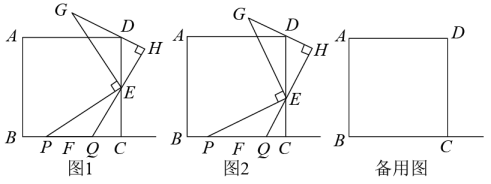
小亮同学在小明研究的基础上，再次动手操作（如图2），（3）将MN延长交BC于点G，将△BMG沿MG折叠，点B刚好落在AD边上点H处，连接GH，把纸片再次展平．请根据小明和小亮的探究，解答下列问题：
1. （1）请写出线段BE和BN的数量关系；
2. （2）请求出∠ABM的度数；
3. （3）请判断四边形BGHM的特殊形状，并说明理由．
答案解析收藏纠错 + 选题
16. (2022八下·潮安期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿 $\text{[math]}$ 方向以 $\text{[math]}$ 秒的速度向点 $\text{[math]}$ 匀速运动，同时点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿 $\text{[math]}$ 方向以 $\text{[math]}$ 秒的速度向点 $\text{[math]}$ 匀速运动，当其中一个点到达终点时，另一点也随之停止运动．设点 $\text{[math]}$ 、 $\text{[math]}$ 运动的时间是 $\text{[math]}$ 秒 $\text{[math]}$ ．过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）线段 $\text{[math]}$ 与 $\text{[math]}$ 大小关系是： $\text{[math]}$ $\text{[math]}$ ，（填“ $\text{[math]}$ ”或“ $\text{[math]}$ ”、“ $\text{[math]}$ ”号）
2. （2）四边形 $\text{[math]}$ 能够成为菱形吗？如果能，求出相应的 $\text{[math]}$ 值，如果不能，说明理由．
3. （3）当t为何值时， $\text{[math]}$ 为直角三角形？请说明理由．
答案解析收藏纠错 + 选题
17. (2022八下·思明期中) 如图①②③，平面内三点O，M，N.如果将线段OM绕点O旋转90°得ON，称点N是点M关于点O的“等直点”，如果OM绕点O顺时针旋转90°得ON，称点N是点M关于点0的“正等直点”，如图②.
1. （1）如图2，在平面直角坐标系中，已知点P（2，1）.
  ①在 $\text{[math]}$ （－1，2）， $\text{[math]}$ （2，－1）， $\text{[math]}$ （1，－2）三点中， ▲ 是点P关于原点O的“等直点”：
  ②若直线 $\text{[math]}$ ： $\text{[math]}$ 交 $\text{[math]}$ 轴于点M，若点N是直线 $\text{[math]}$ 上一点，且点N是点M关于点P的“等直点”，求直线 $\text{[math]}$ 的解析式：
2. （2）如图3，已知点A的坐标为（2，0），点B在直线 $\text{[math]}$ ： $\text{[math]}$ 上，若点B关于点A的“正等直点”C在坐标轴上，D是平面内一点，若四边形ABCD是平行四边形，直接写出点D的坐标.
答案解析收藏纠错 + 选题
18. (2022八下·梁溪期中) 如图，点E，F分别在正方形ABCD的边CD，BC上，且DE=CF，点P在射线BC上（点P不与点F重合）.将线段EP绕点E顺时针旋转90得到线段EG，过点E作GD的垂线QH，垂足为点H，交射线BC于点Q.
1. （1）如图①，若点E是CD的中点，点P在线段BF上，则线段BP，QC，EC的数量关系为；
2. （2）如图②，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立.若成立，请写出证明过程；若不成立，请说明理由；
3. （3）若正方形ABCD的边长为6，AB=3DE，CQ=1，请直接写出线段BP的长.
答案解析收藏纠错 + 选题
19. (2022八下·厦门期中) 已知，点E在正方形ABCD的AB边上（不与点A，B重合），BD是对角线，延长AB到点F，使BF＝AE，过点E作BD的垂线，垂足为M，连接AM，CF.
1. （1）根据题意补全图形，并证明：MB＝ME；
2. （2）若AM＝ $\text{[math]}$ ，求CF的长；
3. （3）用等式表示线段AM， BM， DM之间的数量关系，并证明.
答案解析收藏纠错 + 选题
20. (2022八下·厦门期中) 已知正方形ABCD， E、F分别在DC、BC上，DE＝CF， AE、 DF相交于点G.
1. （1）求证：AE⊥DF；
2. （2）当E是DC中点时，求证：AB＝BG.
答案解析收藏纠错 + 选题
21. (2022八下·厦门期中) 如图1，已知 $\text{[math]}$ ABCD，∠A＝∠BEF＝a，E为AD边上一点，F为DC边上一点，BE＝EF.
1. （1）求证：∠ABE＝∠DEF
2. （2）如图1，若a＝45°，AE＝5， DE＝1，求 $\text{[math]}$ ABCD的面积；
3. （3）如图2，若a＝30°，AE＝4，DE＝2 $\text{[math]}$ .求线段BE的长.
答案解析收藏纠错 + 选题
22. (2022八下·重庆月考) 如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4.
1. （1）如图1，当∠DAG＝30°时，求BE的长；
2. （2）如图2，当点E是BC的中点时，求线段GC的长；
3. （3）如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长.
答案解析收藏纠错 + 选题
23. (2022八下·哈尔滨开学考) 已知在等边三角形ABC中，E、F分别是BC、AC上的两点，连结AE、BF交于D， $\text{[math]}$ ．
1. （1）如图1，求 $\text{[math]}$ 的度数；
2. （2）如图2，G是AB上一点，连结CG交AE、BF于点H、I，若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）在（2）的条件下， $\text{[math]}$ ， $\text{[math]}$ ，求AH的长．
答案解析收藏纠错 + 选题
24. (2022八下·金华月考) 如图，在平行四边形ABCD中，∠BAC＝90°，∠ABC＝45°，在射线CB上取一点E，使得BE＝2BC＝20，当点P从点A匀速运动到点D时，点Q恰好从点C匀速运动到点E. 在线段QC上取点F，使得QF＝2，连结PF，记AP＝ $\text{[math]}$ （ $\text{[math]}$ ）.
1. （1） ①CF＝ ▲（用含 $\text{[math]}$ 的式子表示）
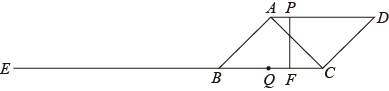
  ②若PF⊥BC，求BQ的长.
2. （2）若以A，B，F，P为顶点的四边形是平行四边形，请求出 $\text{[math]}$ 的值.
3. （3）当点P关于直线AF对称的点恰好落在直线AB上，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
25. (2022八下·长沙月考) 正方形ABCD边长为6，点E在边AB上（点E与点A、B不重合），点F、G分别在边BC、AD上（点F与点B、C不重合），直线FG与DE相交于点H.
1. （1）如图1，若∠GHD=90°，求证：GF=DE；
2. （2）在（1）的条件下，平移直线FG，使点G与点A重合，如图2.联结DF、EF.设CF=x，△DEF的面积为y，用含x的代数式表示y；
3. （3）如图3，若∠GHD=45°，且BE=2AE，求FG的长.
答案解析收藏纠错 + 选题
26. (2022八下·金华月考) 我们规定：有一组邻边相等，且这组邻边的夹角为60°的凸四边形叫做“准筝形”.
1. （1）如图1，在四边形ABCD中，∠A+∠C＝270°，∠D＝30°，AB＝CB，求证：四边形ABCD是“准筝形”；
2. （2）如图2，在“准筝形”ABCD中，AB＝AD，∠BAD＝∠BCD＝60°，BC＝4，CD＝3，求AC的长；
3. （3）如图3，在△ABC中，∠A＝45°，∠ABC＝120°，AB＝3－ $\text{[math]}$ ，设D是△ABC所在平面内一点，当四边形ABCD是“准筝形”时，请直接写出四边形ABCD的面积.
答案解析收藏纠错 + 选题
27. 如图，将△ABC放在每个小正方形的边长为1的网格中，点A、点B、点C均落在格点上
1. （1）线段AB的长度＝；
2. （2）请在如图所示的网格中，用无刻度的直尺，在∠ABC的平分线上找一点P，在BC上找一点Q，使CP+PQ的值最小，并简要说明点P，Q的位置是如何找到的 ▲ （不要求证明）.
答案解析收藏纠错 + 选题
28. 如图，在平面直角坐标系中， $\text{[math]}$ 的边 $\text{[math]}$ 2，且 $\text{[math]}$ 轴，顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .
1. （1）点 $\text{[math]}$ 的坐标是，点 $\text{[math]}$ 的坐标是；(用含 $\text{[math]}$ 的式子表示)
2. （2）若双曲线 $\text{[math]}$ 过 $\text{[math]}$ 的顶点 $\text{[math]}$ 和 $\text{[math]}$ ，求该双曲线的表达式；
3. （3）若 $\text{[math]}$ 与双曲线 $\text{[math]}$ 总有公共点，写出 $\text{[math]}$ 的取值范闱.
答案解析收藏纠错 + 选题
29. (2022八下·浙江) 正方形ABCD中，E是对角线BD 上一点，过点E作EF⊥AE交射线CB于点F，连结CE.
1. （1）如图，已知点F在线段BC上，①若AB=BE，求∠DAE度数；②求证：CE=EF.
2. （2）已知正方形的边长为2，且BC=2BF，请直接写出线段 DE的长.
答案解析收藏纠错 + 选题
30. 如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG//CD交BE于点G，连结CG.
1. （1）求证：四边形CEFG是菱形；
2. （2）若AB=6，AD=10，求四边形CEFG的面积.
答案解析收藏纠错 + 选题

试卷信息