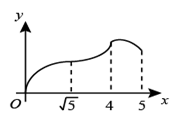
①求m的取值范围;
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单长度后得到的点Q' 也在G上时,求G在≤
≤
的图象的最高点的坐标.
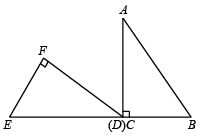
①倘若 , 且在
的右侧,两抛物线都上升,求
的取值范围;
②在原抛物线上,新抛物线与
轴交于
,
时,求
点坐标.
(参考数据: ,
)
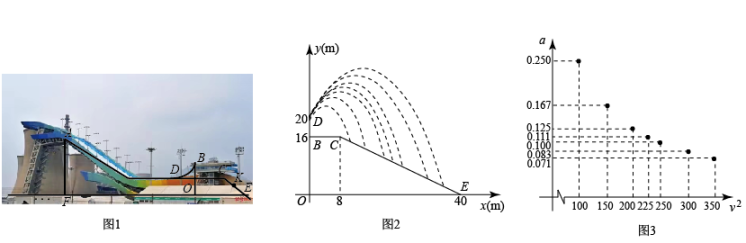
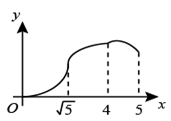
①猜想a关于的函数类型,求函数表达式,并任选一对对应值验证.
②当v为多少m/s时,运动员的成绩恰能达标(精确到1m/s)?

 B .
B .  C .
C .  D .
D . 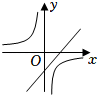


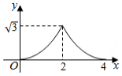 B .
B . 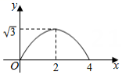 C .
C . 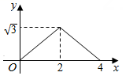 D .
D . 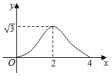
 B .
B . 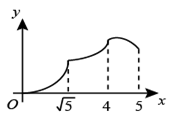 C .
C .  D .
D .