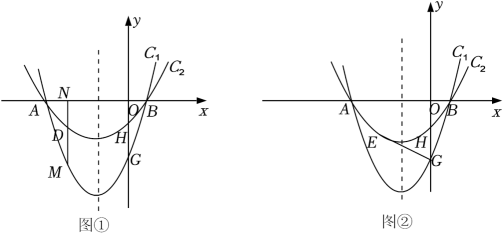

①求点和点
的坐标;
②若点 ,
分别为抛物线
和抛物线
上
,
之间的动点(点
,
与点
,
不重合),试求四边形
面积的最大值.
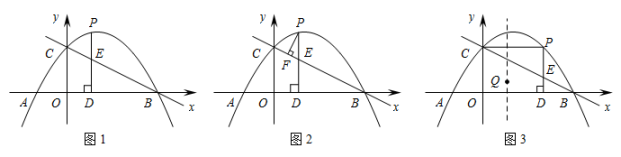
①如图1,直线DC交直线x=1于点E,连接OE.求证:AD∥OE;
②如图2,点P(2,﹣5)为抛物线y=ax2+bx+3(a≠0)上一点,过点P作PG⊥x轴,垂足为点G.直线DP交直线x=1于点H,连接HG.求证:AD∥HG;
猜想:作MN⊥x轴于N,直线DM交直线x=1于Q,则QN∥AD,证明见解析

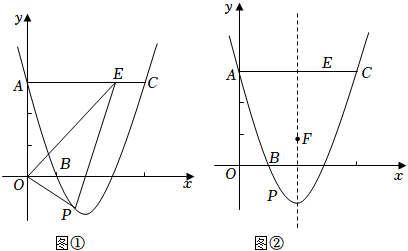
(Ⅰ)求该抛物线所表示的二次函数表达式;
(Ⅱ)若点P是抛物线上一动点(与点A不重合),过点P作PH⊥x轴于点H,与线段AB交于点M,是否存在点P使得点M是线段PH的三等分点?若存在,请求出点P的坐标:若不存在,请说明理由.
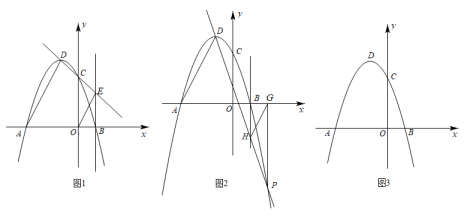
①求点P的坐标;
②直线(m是常数,
)与抛物线相交于点M,与
相交于点G,当
取得最大值时,求点M,G的坐标;