备考2023年中考数学绍兴卷变式阶梯训练：17-20题

更新时间：2023-04-06 浏览次数：223 类型：三轮冲刺

一、第十七题

1. (2022·绍兴)
1. （1）计算： $\text{[math]}$ ．
2. （2）解方程组 $\text{[math]}$
答案解析收藏纠错 + 选题
2. (2022·秀洲模拟)
1. （1）计算：2^-1-2022⁰+ sin30°
2. （2）解方程组： $\text{[math]}$
答案解析收藏纠错 + 选题
3. (2023·江北模拟)
1. （1）计算：sin30°-（ $\text{[math]}$ -2）⁰+2^-¹；
2. （2）解方程组： $\text{[math]}$ .
答案解析收藏纠错 + 选题
4. (2022·锡山模拟) 计算：
1. （1）计算： $\text{[math]}$ ﹣3tan60°+（π﹣2）⁰；
2. （2）解方程组： $\text{[math]}$ .
答案解析收藏纠错 + 选题
5. (2022·龙游模拟)
1. （1）计算： $\text{[math]}$
2. （2）解方程组： $\text{[math]}$
答案解析收藏纠错 + 选题
6. (2021·萧山模拟)
1. （1）计算： $\text{[math]}$ ﹣|﹣2|﹣tan30°+（ $\text{[math]}$ ）^﹣¹；
2. （2）解方程组： $\text{[math]}$ .
答案解析收藏纠错 + 选题
7. (2019·越城模拟)
1. （1）计算： $\text{[math]}$ ；
2. （2）解方程组： $\text{[math]}$
答案解析收藏纠错 + 选题

二、第十八题

8. (2022·绍兴) 双减政策实施后，学校为了解八年级学生每日完成书面作业所需时长x（单位：小时）的情况，在全校范围内随机抽取了八年级若干名学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息解答下列问题．

八年级学生每日完成书面作业所需时长情况的统计表

组别	所需时长（小时）	学生人数（人）
A	$\text{[math]}$	15
B	$\text{[math]}$	m
C	$\text{[math]}$	n
D	$\text{[math]}$	5

八年级学生每日完成书面作业所需时长情况的扇形统计图

（1）求统计表中m，n的值．
（2）已知该校八年级学生有800人，试估计该校八年级学生中每日完成书面作业所需时长满足 $\text{[math]}$ 的共有多少人．

答案解析收藏纠错 + 选题

9. (2023·青岛模拟) 2022年末，中国迎来第一波疫情高峰．为加强同学们的防护意识，某校举行了以“疫情防护”为主题的知识竞赛活动．发现该校全体学生的竞赛成绩（百分制）均不低于60分，现从中随机抽取n名学生的竞赛成绩进行整理和分析（成绩得分用x表示，共分成四组），并绘制成如下的竞赛成绩分组统计表和扇形统计图，下面为部分数据：其中“ $\text{[math]}$ ”这组的部分数据（从小到大排序）如下：80，82，82，83，83，84，85，85，85，86，87，87，87，88，88……其中“ $\text{[math]}$ ”这组的数据如下：90，92，93，95，95，96，96，96，97，100．
竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分
1
$\text{[math]}$
8
65
2
$\text{[math]}$
a
75
3
$\text{[math]}$
b
88
4
$\text{[math]}$
10
95
根据以上信息，回答下列问题：
1. （1）下列说法正确的是____．
  
  A . 样本为n名学生 B . a＝12 C . m＝40
2. （2） “ $\text{[math]}$ ”这组的数据的众数是．
3. （3）随机抽取的这n名学生竞赛成绩的中位数是；平均分是；
4. （4）若学生竞赛成绩达到96分以上（含96分）获奖，请你估计全校1200名学生中获奖的人数．
答案解析收藏纠错 + 选题
10. (2023·岳阳楼模拟) 在体育活动课中，体育老师随机抽取了九年级甲、乙两班部分学生进行某体育项目的测试，并对成绩进行统计分析，绘制了频数分布表，请你根据表中的信息完成下列问题：
分组
频数
频率
第一组（不及格）
3
0.15
第二组（中）
b
0.20
第三组（良）
7
0.35
第四组（优）
6
a
1. （1）频数分布表中 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）如果该校九年级共有学生900人，估计该校该体育项目的成绩为良和优的学生有多少人？
3. （3）已知第一组中有两个甲班学生，第二组中只有一个乙班学生，老师随机从这两个组中各选一名学生对体育活动课提出建议，则所选两人正好是甲班和乙班各一人的概率是多少？
答案解析收藏纠错 + 选题

11. (2022·江干模拟) 针对新型冠状病毒事件，九（1）班全体学生参加学校举行的“珍惜生命，远离病毒”知识竞赛后，班长对本班成绩进行分析，制作如下的频数分布表和频数分布条形统计图 $\text{[math]}$ 未完成 $\text{[math]}$ 除了60到70之间学生成绩尚未统计，还有6名学生成绩如下：90，96，98，99，99，99班长根据情况画出的扇形统计图如下：

类别	分数段	频数 $\text{[math]}$ 人数 $\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	16
$\text{[math]}$	$\text{[math]}$	24
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

（1）九（1）班有多少名学生？
（2）求出 $\text{[math]}$ 、 $\text{[math]}$ 的值？并请补全条形统计图.
（3）全校共有720名学生参加初赛，估计该校成绩 $\text{[math]}$ 范围内的学生有多少人？
（4）九（1）班甲、乙、丙三位同学的成绩并列第一，现选两人参加决赛，求恰好选中甲，乙两位同学的概率.

答案解析收藏纠错 + 选题

12. (2023·茂南模拟) 某校为了了解七年级800名学生跳绳情况，从七年级学生中随机抽取部分学生进行1分钟跳绳测试，并对测试成绩进行统计分析，得到如下所示的频数分布表：
跳绳个数 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
频数
16
30
50
$\text{[math]}$
24
所占百分比
8%
15%
25%
40%
$\text{[math]}$
请根据尚未完成的表格，解答下列问题：
1. （1）本次随机抽取了名学生进行1分钟跳绳测试，表中a=，b=；
2. （2）补全频数直方图；
3. （3）若绘制“七年级学生1分钟跳绳测试成绩扇形统计图”，则测试成绩在 $\text{[math]}$ 个所对应扇形的圆心角的度数是；
4. （4）若跳绳个数超过140个为优秀，则该校七年级学生1分钟跳绳成绩优秀的约有多少人？
答案解析收藏纠错 + 选题
13. (2022九上·南城期中) 为了有效落实“双减”政策，某校随机抽取部分学生，开展了“书面作业完成时间”问卷调查．根据调查结果，绘制了如下不完整的统计图表：
频数分布统计表
组别
时间 $\text{[math]}$ 分钟 $\text{[math]}$
频数
$\text{[math]}$
$\text{[math]}$
6
$\text{[math]}$
$\text{[math]}$
14
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
4
根据统计图表提供的信息解答下列问题：
1. （1）频数分布统计表中的 $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ；并补全频数分布直方图；
2. （2）已知该校有1000名学生，估计书面作业完成时间在60分钟以上(含60分钟)的学生有多少人？
3. （3）若 $\text{[math]}$ 组有两名男同学、两名女同学，从中随机抽取两名学生了解情况，请用列表或画树状图的方法，求出抽取的两名同学恰好是一男一女的概率．
答案解析收藏纠错 + 选题

14. (2022·顺城模拟) 为庆祝中国共产党建党100周年，某校开展了党史知识竞赛．某年级随机选出了一个班的初赛成绩进行统计，得到如下统计图表，已知在扇形统计图 $\text{[math]}$ 分数段对应的扇形六圆心角为 $\text{[math]}$ ．某校组织读书征文比赛活动，评选出一、二、三等奖若干名，并绘成如图所示的统计表和扇形统计图（不完整），请你根据图中信息解答下列问题：

统计表

分段	成绩范围（分）	频数	频率
$\text{[math]}$	90~100	$\text{[math]}$	0.1
$\text{[math]}$	80~89	20	$\text{[math]}$
$\text{[math]}$	70~79	$\text{[math]}$	0.3
$\text{[math]}$	70分以下	10	$\text{[math]}$

注：90~100表示成绩 $\text{[math]}$ ，满足 $\text{[math]}$ ，以下相同．

扇形统计图

（1）在统计表中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
（2）若该年级参加初赛的学生共有2000人，根据以上统计数据估计该年级成绩在90分及以上的学生人数；
（3）若统计表 $\text{[math]}$ 分数段的男生比女生少1人，从 $\text{[math]}$ 段中任选2人参加复赛，请用列表法或画树状图的方法，求出恰好抽到1名男生和1名女生的概率．

答案解析收藏纠错 + 选题

三、第十九题

15. 一个深为6米的水池积存着少量水，现在打开水阀进水，下表记录了2小时内5个时刻的水位高度，其中x表示进水用时（单位：小时），y表示水位高度（单位：米）．

x

0

0.5

1

1.5

2

y

1

1.5

2

2.5

3

为了描述水池水位高度与进水用时的关系，现有以下三种函数模型供选择： $\text{[math]}$ （ $\text{[math]}$ ），y=ax²+bx+c ( $\text{[math]}$ )， $\text{[math]}$ （ $\text{[math]}$ ）．
1. （1）在平面直角坐标系中描出表中数据对应的点，再选出最符合实际的函数模型，求出相应的函数表达式，并画出这个函数的图象．
2. （2）当水位高度达到5米时，求进水用时x．
答案解析收藏纠错 + 选题
16. (2021·嵊州模拟) 某太阳能热水器水箱的最大蓄水量为160升，在没有放水的情况下匀速注水.已知水箱的蓄水量y（升）与注水时间x（分）

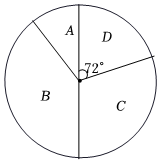
x（分）

0

4

8

12

……

y（升）

20

60

100

140

……
1. （1）通过描点法判断变量x，y是否满足或近似地满足一次函数关系式.如果是，求y关于x的函数表达式.
2. （2）按上述速度注满水箱，需要多少分钟？
答案解析收藏纠错 + 选题
17. (2022九上·嘉兴期中) 习近平总书记在全国劳动模范和先进工作者表彰大会上讲话：劳动教育应纳入人才培养全过程.为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，发现其平均单株产量 $\text{[math]}$ 千克与每平方米种植的株数 $\text{[math]}$ ，且 $\text{[math]}$ 为整数 $\text{[math]}$ 构成一种函数关系；每平方米种植2株时，平均单株产量为5千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量将减少0.5千克.
1. （1）求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式；
2. （2）每平方米种植多少株时，能获得最大的产量？最大产量为多少千克？
答案解析收藏纠错 + 选题
18. (2022九上·舟山月考) 某超市经销一种销售成本为每件40元的商品，据市场调查分析，如果按每件50元销售，一周能售出500件，若销售单价每涨1元，每周销量就减少10件，设销售单价为x元（ $\text{[math]}$ ），一周的销售量为y件．
1. （1）写出y与x的函数关系式：（标明x的取值范围）；
2. （2）设一周的销售利润为S，写出S与x的函数关系式，并确定当单价是多少时利润最大；
3. （3）在超市对该种商品投入不超过12000元的情况下，使得一周销售利润为8000元，销售单价应定为多少元？
答案解析收藏纠错 + 选题
19. (2022·路南模拟) 小明、小亮利用遥控器在电子屏上分别玩甲、乙两个小飞机，甲、乙两个小飞机分别从水平线起点和距水平线起点高15m处同时出发，匀速上升60min．如图是甲、乙两个小飞机所在位置的高度y（单位：m）与飞机上升时间x（单位：min）的函数图象．
1. （1）求这两个小飞机在上升过程中y关于x的函数解析式；
2. （2）当这两个小飞机的高度相差18m时，求上升的时间．
答案解析收藏纠错 + 选题
20. (2022·富拉尔基) 甲、乙两车分别从相距360km的富区、哈市两地出发，匀速行驶，先相向而行，乙车在甲车出发1h后出发，到达富区后停止行驶，甲车到达哈市后，立即按原路原速返回富区（甲车调头的时间忽略不计），甲、乙两车距哈市的路程 $\text{[math]}$ （单位：km）， $\text{[math]}$ （单位：km）与甲车出发时间x（单位：h）之间的函数图象如图所示，请结合图象信息解答下列问题：
1. （1）乙车的行驶速度是， $\text{[math]}$ ；乙车距哈市的路程 $\text{[math]}$ 与甲车出发时间x之间的函数解析式是（不写自变量的取值范围）
2. （2）甲车与乙车第一次相遇时，距离富区的路程是多少千米？
3. （3）甲车出发多少小时后两车相距为100km？请直接写出答案．
答案解析收藏纠错 + 选题
21. (2022·温州模拟) 某中学为筹备校庆，准备印制一批纪念册.该纪念册每册需要10张纸，其中4张彩色页，6张黑白页.印刷该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为2200元，印刷费与印数的关系见表.

印数a（千册）

$\text{[math]}$

$\text{[math]}$

彩色（元/张）

2.1

2

黑白（元/张）

0.8

0.5
1. （1）若印制2千册，则共需多少元？
2. （2）该校先印制了x千册纪念册，后发现统计失误，补印了y（ $\text{[math]}$ ）千册纪念册，且补印时无需再次缴纳制版费，学校发现补印的单册造价便宜了，但两次缴纳费用恰好相同.
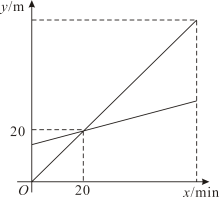
  ①用含x的代数式表示y.
  
  ②若该校没有统计错误，一次性打印全部纪念册，最少需要多少钱？
答案解析收藏纠错 + 选题

四、第二十题

22. (2023·铜仁模拟) 圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至.图2是一个根据某市地理位置设计的圭表平面示意图，表 AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37° ，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．
1. （1）求∠BAD的度数．
2. （2）求表AC的长（最后结果精确到0.1米）．
  （参考数据：sin37°≈ $\text{[math]}$ ，cos37°≈ $\text{[math]}$ ，tan37°≈ $\text{[math]}$ ，tan84°≈ $\text{[math]}$ ）
答案解析收藏纠错 + 选题
23. (2023九下·南昌期中) 如图1是一张折叠型方桌子，图2是其侧面结构示意图，支架 $\text{[math]}$ 与 $\text{[math]}$ 交于点O，测得 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）将桌子放平后，要使 $\text{[math]}$ 距离地面的高为 $\text{[math]}$ ，求两条桌腿需叉开角度 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2022·南开模拟) 随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量翡翠湖某处东西岸边 $\text{[math]}$ ， $\text{[math]}$ 两点之间的距离．如图所示，小星站在湖边的 $\text{[math]}$ 处遥控无人机，无人机在 $\text{[math]}$ 处距离地面的飞行高度是 $\text{[math]}$ ，此时从无人机测得岸边 $\text{[math]}$ 处的俯角为 $\text{[math]}$ ，他抬头仰视无人机时，仰角为 $\text{[math]}$ ，若小星的身高 $\text{[math]}$ ， $\text{[math]}$ （点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一平面内）．
1. （1）求仰角 $\text{[math]}$ 的正弦值；
2. （2）求 $\text{[math]}$ ， $\text{[math]}$ 两点之间的距离（结果精确到 $\text{[math]}$ ）．（ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
25. (2023·泗洪模拟) 如图，梯形 $\text{[math]}$ 是某水坝的横截面示意图，其中 $\text{[math]}$ ，坝顶 $\text{[math]}$ ，坝高 $\text{[math]}$ ，迎水坡 $\text{[math]}$ 的坡度为 $\text{[math]}$ .
1. （1）求坝底 $\text{[math]}$ 的长；
2. （2）为了提高堤坝防洪抗洪能力，防汛指挥部决定在背水坡加固该堤坝，要求坝顶加宽 $\text{[math]}$ ，背水坡坡角改为 $\text{[math]}$ .求加固总长5千米的堤坝共需多少土方？（参考数据： $\text{[math]}$ ；结果精确到 $\text{[math]}$ ）
答案解析收藏纠错 + 选题
26. (2023·商河模拟) 图1是某型号挖掘机，该挖掘机是由基座、主臂和伸展臂构成．图2是某种工作状态下的侧面结构示意图（ $\text{[math]}$ 是基座的高， $\text{[math]}$ 是主臂， $\text{[math]}$ 是伸展臂， $\text{[math]}$ ）．已知基座高度 $\text{[math]}$ 为 $\text{[math]}$ ，主臂 $\text{[math]}$ 长为 $\text{[math]}$ ，测得主臂伸展角 $\text{[math]}$ ．
（参考数据： $\text{[math]}$ ）
1. （1）求点P到地面的高度；
2. （2）若挖掘机能挖的最远处点Q到点N的距离为 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
27. (2023·徐汇模拟) 如图，是一个放置于水平桌面的平板支架的示意图，底座的高 $\text{[math]}$ 为 $\text{[math]}$ ，宽 $\text{[math]}$ 为 $\text{[math]}$ ，点A是 $\text{[math]}$ 的中点，连杆 $\text{[math]}$ 的长度分别为 $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ ，且连杆 $\text{[math]}$ 与 $\text{[math]}$ 始终在同一平面内．
1. （1）求点C到水平桌面的距离；
2. （2）产品说明书提示，若点D与A的水平距离超过 $\text{[math]}$ 的长度，则该支架会倾倒．现将 $\text{[math]}$ 调节为 $\text{[math]}$ ，此时支架会倾倒吗？（参考数据∶ $\text{[math]}$ ）
答案解析收藏纠错 + 选题
28. (2022·坪山模拟) 如图1，某学校开展“交通安全日”活动．在活动中，交警叔叔向同学们展示了大货车盲区的分布情况，并提醒大家：坐在驾驶室的司机根本看不到在盲区中的同学们，所以一定要远离大货车的盲区，保护自身安全．小刚所在的学习小组为了更好的分析大货车盲区的问题，将图1用平面图形进行表示，并标注了测量出的数据，如图2．在图2中大货车的形状为矩形，而盲区1为梯形，盲区2、盲区3为直角三角形，盲区4为正方形．

请你帮助小刚的学习小组解决下面的问题：
1. （1）盲区1的面积约是m²；盲区2的面积约是m²；（ $\text{[math]}$ ≈1.4， $\text{[math]}$ ≈1.7，sin25°≈0.4，cos25°≈0.9，tan25°≈0.5，结果保留整数）
2. （2）如果以大货车的中心A点为圆心，覆盖所有盲区的半径最小的圆为大货车的危险区域，请在图2中画出大货车的危险区域．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

备考2023年中考数学绍兴卷变式阶梯训练：17-20题

副标题：

*注意事项：

备考2023年中考数学绍兴卷变式阶梯训练：17-20题

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

组别	竞赛成绩分组	频数	平均分
1	$\text{[math]}$	8	65
2	$\text{[math]}$	a	75
3	$\text{[math]}$	b	88
4	$\text{[math]}$	10	95

分组	频数	频率
第一组（不及格）	3	0.15
第二组（中）	b	0.20
第三组（良）	7	0.35
第四组（优）	6	a

跳绳个数 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
频数	16	30	50	$\text{[math]}$	24
所占百分比	8%	15%	25%	40%	$\text{[math]}$

组别	时间 $\text{[math]}$ 分钟 $\text{[math]}$	频数
$\text{[math]}$	$\text{[math]}$	6
$\text{[math]}$	$\text{[math]}$	14
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	4

印数a（千册）	$\text{[math]}$	$\text{[math]}$
彩色（元/张）	2.1	2
黑白（元/张）	0.8	0.5

x	0	0.5	1	1.5	2
y	1	1.5	2	2.5	3

x（分）	0	4	8	12	……
y（升）	20	60	100	140	……