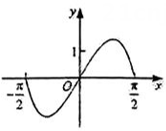
 B .
B . 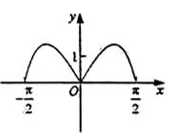 C .
C . 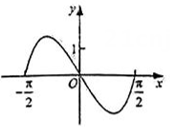 D .
D . 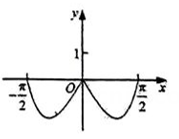
①;
②;
③在
上单调递增;
④为了得到的图象,只需将
的图象向右平移
个单位长度.
以上四个说法中,正确的个数为( )
① ;
② .

参考数据: ,
,
.参考公式:对于一组数据
,
,…,
,回归方程
中的斜率和截距的最小二乘估计公式分别为
,
.
| 培养基质量x(克) | 20 | 40 | 50 | 60 | 80 |
| 细菌A的最大承载量Y(单位) | 300 | 400 | 500 | 600 | 700 |

参考数据: ,
,
,
.参考公式:回归方程
中斜率和截距的最小二乘估计公式分别为:
,
.
附:回归直线的斜率和截距的最小二乘估计公式分别为: .
②向量 ,
,且
,
;
③函数 的图象经过点
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知_________________,且函数 的图象相邻两条对称轴之间的距离为
.
注:如果选择多个条件分别解答,按第一个解答计分.