备战2024年中考数学细点逐一突破真题训练第16章概率统计初...

更新时间：2024-03-13 浏览次数：70 类型：一轮复习

一、数据的收集与整理

1. (2024九下·福州开学考) 下列事件中，不是随机事件的是（）

A . 射击运动员射击一次，命中靶心 B . 打开电视机，它正在播广告 C . 购买一张彩票，中奖 D . 从只装有红球的布袋中，任意摸出一个球，恰是白球

答案解析收藏纠错 + 选题
2. (2024九下·珠晖模拟) 下列事件为必然事件的是（）

A . 中秋节晚上一定能看到月亮 B . 明天的气温一定会比今天的高 C . 某彩票中奖率是1％，买100张彩票一定会中奖。 D . 地球上，上抛的篮球一定会下落

答案解析收藏纠错 + 选题
3. (2023·咸宁模拟) 下列说法正确的是（）

A . 打开电视机，它正在播广告是必然事件 B . 掷一枚质地均匀的硬币，正面朝上的概率可能为0 C . 一组数据“5，4，6，2，7，4，3”的众数是4，中位数是2 D . 从全校1500名学生中抽取100名调查了解寒假阅读情况，抽取的样本容量为100

答案解析收藏纠错 + 选题
4. (2024七上·安乡县期末) 下列调查方式中，适合的是（）

A . 《新闻联播》电视栏目的收视率，采用普查方式 B . 某小型企业给在职员工做工作服前进行尺寸大小调查，采用抽样调查方式 C . 一批灯泡的使用寿命，采用普查方式 D . 环保部门对安乡珊泊湖水质情况的调查，采用抽样调查方式

答案解析收藏纠错 + 选题
5. (2024七上·光明期末) 学习了频数分布直方图后，光明区某数学兴趣小组对某农场的西红柿大棚中每株西红柿秧结的小西红柿的个数做了调查.兴趣小组随机收集了这个农场西红柿大棚其中30株西红柿秧上结的小西红柿的个数如下：
28
62
54
39
32
47
68
27
65
43
52
59
67
59
45
42
79
51
54
25
82
18
39
32
64
74
49
37
39
52
1. （1）数学兴趣小组采用的调查方式是；（填“普查”或“抽样调查”）
2. （2）将调查的30株西红柿秧上小西红柿的个数按组距为10将数据分组，列表如下：
  分组
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  频数
  2
  $\text{[math]}$
  7
  $\text{[math]}$
  5
  3
  2
  （16～26表示大于等于16同时小于26，其它分组中的“～”均表示这一含义）写出表中 $\text{[math]}$ 和 $\text{[math]}$ 的值；
3. （3）根据以上的分组，画出频数分布直方图.
答案解析收藏纠错 + 选题

二、常规概率题型

6. (2024九下·哈尔滨模拟) 在一个不透明的袋子里装有2个红球和5个白球，它们除颜色外都相同，从中任意摸出1个球，则摸出的球为红球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·长沙月考) 从正三角形、正方形、正五边形、正六边形中任选一个，选中的恰好既是轴对称图形，又是中心对称图形的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. 甲、乙两位同学相约打乒乓球．
1. （1）有款式完全相同的4个乒乓球拍 $\text{[math]}$ 分别记为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若甲先从中随机选取1个，乙再从余下的球拍中随机选取1个，求乙选中球拍C的概率；
2. （2）双方约定：两人各投掷一枚质地均匀的硬币，如果两枚硬币全部正面向上或全部反面向上，那么甲先发球，否则乙先发球 $\text{[math]}$ 这个约定是否公平？为什么？
答案解析收藏纠错 + 选题

三、跨学科概率问题

9. (2023九下·淮北月考) 将分别写有“魅”“力”“安”“徽”四个汉字的小球装在一个不透明的口袋中，这些球除汉字不同外其他完全相同，每次摸球前先搅匀，随机摸出 $\text{[math]}$ 个球，放回后再随机摸出 $\text{[math]}$ 个球，两次摸出的球上的汉字可以组成“安徽”的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023·随州模拟) 看了《田忌赛马》故事后，数学兴趣小组用数学模型来分析：齐王与田忌的上中下三个等级的三匹马综合指标数如表，每匹马只赛一场，综合指标的两数相比，大数为胜，三场两胜则赢，已知齐王的三匹马出场顺序为6、4、2，若田忌的三匹马随机出场，则田忌能赢得比赛的概率为（）
马匹等级
下等马
中等马
上等马
齐王
2
4
6
田忌
1
3
5

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023·安庆模拟) 如图是某电路图，随机闭合开关 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中的任意 $\text{[math]}$ 个，能同时使两盏小灯泡发光的概率是（）

A . $\text{[math]}$
B . $\text{[math]}$
C . $\text{[math]}$
D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023·合肥模拟) 同一元素中质子数相同，中子数不同的各种原子互为同位素，如 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 与 $\text{[math]}$ ．在一次制取 $\text{[math]}$ 的实验中， $\text{[math]}$ 与 $\text{[math]}$ 的原子个数比为 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的原子个数比为 $\text{[math]}$ ，若实验恰好完全反应生成 $\text{[math]}$ ，则反应生成 $\text{[math]}$ 的概率（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2024·安顺模拟) 如图，电路图有4只未闭合的开关，一个电源和一个小灯泡，已知电路图上的每个部分都能正常工作，任意闭合其中两只开关，使得小灯泡发光的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2023·蚌埠模拟) 如图，在正六边形转盘中，有两个正三角形涂有阴影， $\text{[math]}$ 为可绕点O自由转动的指针，转动指针（若指针恰好停在分界线上，则重新转动），指针落在有阴影的区域内的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2023·太和模拟) 如图所示的电路图中，当随机闭合 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中的两个开关时，灯泡能发光的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

四、平均数、众数、中位数、方差性质应用

16. (2024八上·福田期末) 甲、乙两名射击运动员分别进行了相同次数的射击训练，如果将甲、乙两人射击环数的平均数分别记作 $\text{[math]}$ 和 $\text{[math]}$ ，方差分别记作 $\text{[math]}$ 和 $\text{[math]}$ ，那么下列描述能说明甲运动员成绩较好且更稳定的是（）

A . $\text{[math]}$ 且 $\text{[math]}$ B . $\text{[math]}$ 且 $\text{[math]}$ C . $\text{[math]}$ 且 $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2024·德阳模拟) 甲、乙两人在相同条件下，各射击10次，经计算，甲射击成绩的平均数是8环，方差是 $\text{[math]}$ $\text{[math]}$ ；乙射击成绩的平均数是8环，方差是 $\text{[math]}$ $\text{[math]}$ ．下列说法不一定正确的是（）

A . 甲、乙成绩的总环数相同 B . 甲的成绩比乙的成绩稳定 C . 甲、乙成绩的中位数可能相同 D . 甲、乙成绩的众数一定相同

答案解析收藏纠错 + 选题
18. 已知一组数据x₁，x₂，x₃，平均数是2，方差是3，则另一组数2x₁-1，2x₂-1，2x₃-1的平均数和方差分别是（）

A . 2， $\text{[math]}$ B . 3，3 C . 3，12 D . 3，4

答案解析收藏纠错 + 选题
19. (2024八上·福田期末) 为了解八年级学生的体质健康状况，某校对八年级 $\text{[math]}$ 班 $\text{[math]}$ 名同学进行了体质检测 $\text{[math]}$ 满分 $\text{[math]}$ 分，最低 $\text{[math]}$ 分 $\text{[math]}$ ，并按照男女把成绩整理如图：

八年级 $\text{[math]}$ 班体质检测成绩分析表

平均数
中位数
众数
方差
男生
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
女生
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
1. （1）求八年级 $\text{[math]}$ 班的女生人数；
2. （2）根据统计图可知， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
3. （3）若该校八年级一共有 $\text{[math]}$ 人，则估计得分在 $\text{[math]}$ 分及 $\text{[math]}$ 分以上的人数共有多少人？
答案解析收藏纠错 + 选题
20. 有下列说法：①数据7，7，6，5，4的众数是2；②若数据 $\text{[math]}$ 的平均数是 $\text{[math]}$ ，则 $\text{[math]}$ ③数据1，2，3，4，5，6的中位数是3和4；④数据21，22，23，24，25的方差是2.其中正确的是（）

A . ①③ B . ②④ C . ①②④ D . ②③④

答案解析收藏纠错 + 选题
21. 某校举行了“少年强则国强”作文大赛，并组织七、八年级各200名学生参加.现分别在七、八两个年级中各随机抽取10名学生，记录并整理了这部分学生的比赛成绩.
【收集数据】
七年级10名同学的比赛成绩分别为72，83，72，92，79，69，78，85，76，94；
八年级10名同学的比赛成绩分别为86，71，93，83，80，74，75，80，76，82.
【整理数据】
两组数据各分数段人数如下表所示：
成绩x(分)
60≤x<70
70≤x<80
80≤x<90
90≤x<100
七年级
1
5
a
2
八年级
0
4
5
1
【分析数据】
两组数据的平均数、中位数、众数、方差如下表所示：

平均数(分)
中位数(分)
众数(分)
方差(分²)
七年级
80
c
72
64.4
八年级
b
80
d
37.6
【问题解决】
根据以上信息解答下列问题：
1. （1） a=，c=，b=，d=.
2. （2）请你估计哪个年级的比赛成绩更稳定.
3. （3）按照比赛规定，90分及以上算优秀，请估计这两个年级比赛成绩达到优秀的学生人数是多少.
答案解析收藏纠错 + 选题

五、树状图、列表法概率应用

22. (2023九上·南山期中) 某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况，进行了统计调查 $\text{[math]}$ 随机调查了某班所有同学最喜欢的节目 $\text{[math]}$ 每名学生必选且只能选择四类节目中的一类 $\text{[math]}$ 并将调查结果绘成如下不完整的统计图 $\text{[math]}$ 根据两图提供的信息，回答下列问题：
1. （1）最喜欢娱乐类节目的有人，图中 $\text{[math]}$ ；
2. （2）请补全条形统计图；
3. （3）根据抽样调查结果，若该校有1800名学生，请你估计该校有多少名学生最喜欢娱乐类节目；
4. （4）在全班同学中，有甲、乙、丙、丁等同学最喜欢体育类节目，班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛，请用列表法或树状图求同时选中甲、乙两同学的概率．
答案解析收藏纠错 + 选题
23. (2023九上·新津月考) 某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：
1. （1）在这次调查中，喜欢篮球项目的同学有人，在扇形统计图中，“乒乓球”的百分比为%，如果学校有800名学生，估计全校学生中有人喜欢篮球项目.
2. （2）请将条形统计图补充完整.
3. （3）在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
答案解析收藏纠错 + 选题

24. (2023·酒泉模拟) 4月23日是世界读书日，习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气．”某校响应号召，鼓励师生利用课余时间广泛阅读，该校文学社为了解学生课外阅读情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：

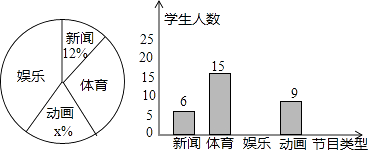
一、数据收集，从全校随机抽取20学生，进行每周用于课外阅读时间的调查，数据如下（单位： $\text{[math]}$ ）：

30	60	81	50	44	110	130	146	80	100
60	80	120	140	75	81	10	30	81	92

二、整理数据，按如下分段整理样本数据并补全表格：

课外阅读时间 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
等级	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
人数	3	$\text{[math]}$	8	$\text{[math]}$

三、分析数据，补全下列表格中的统计量：

平均数	中位数	众数
80	$\text{[math]}$	81

四、得出结论：

①表格中的数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；

②用样本中的统计量估计该校学生每周用于课外阅读时间的等级为；

③如果该校现有学生400人，估计等级为“ $\text{[math]}$ ”的学生有人；

④假设平均阅读一本课外书的时间为320分钟，请你用样本平均数估计该校学生每人一年（按52周计算）

平均阅读本课外书．

答案解析收藏纠错 + 选题

25. (2023·长沙模拟) 某校以中国传统节日端午节为契机，组织全体学生参加包粽子劳动体验活动，随机调查了部分学生，对他们每个人平均包一个粽子的时长进行统计，并根据统计结果绘制成如下不完整的统计图表．

等级	时长（单位：分种）	人数	所占百分比
A	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
B	$\text{[math]}$	$\text{[math]}$
C	$\text{[math]}$		$\text{[math]}$
D	$\text{[math]}$		$\text{[math]}$

根据图表信息，解答下列问题：

（1）本次调查的学生总人数为，表中x的值为；
（2）该校共有500名学生，请你估计等级为B的学生人数；
（3）本次调查中，等级为A的4人中有两名男生和两名女生，若从中随机抽取两人进行活动感想交流，请利用画树状图或列表的方法，求恰好抽到一名男生和一名女生的概率．

答案解析收藏纠错 + 选题

26. (2023·长沙模拟) 近几年，新型冠状病毒感染的肺炎疫情牵动着全国人民的心，为了提高意识，共克时艰，共渡难关，某校开展了“全民行动·共同抗疫”的自我防护知识网上答题竞赛，现从该校七、八年级中各随机抽取 $\text{[math]}$ 名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组： $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ），下面给出了部分信息：
七年级 $\text{[math]}$ 名学生的竞赛成绩是； $\text{[math]}$
八年级 $\text{[math]}$ 名学生的竞赛成绩在 $\text{[math]}$ 组中的数据是： $\text{[math]}$
八年级抽取的学生竞赛成绩扇形统计图

七、八年级抽取的学生竞赛成绩统计表
年级
七年级
八年级
平均数
$\text{[math]}$
$\text{[math]}$
中位数
$\text{[math]}$
$\text{[math]}$
方差
$\text{[math]}$
$\text{[math]}$
根据以上信息，解答下列问题；
1. （1） $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）该校七、八年级共 $\text{[math]}$ 人参加了此次网上答题竞赛活动，估计参加竞赛活动成绩优秀（ $\text{[math]}$ ）的学生人数是多少？
3. （3）如果从七年级 $\text{[math]}$ 分（含 $\text{[math]}$ 分）以上的四名学生中抽取两名学生参加市里的知识竞赛，请用列表法或树状图法求恰好抽中 $\text{[math]}$ 分的学生参赛的概率是多少？（用 $\text{[math]}$ 表示 $\text{[math]}$ 分， $\text{[math]}$ 表示 $\text{[math]}$ 分）
答案解析收藏纠错 + 选题
27. (2023·黄冈模拟) 前两年，“碳中和，碳达峰”成为高频热词，为了解学生对“碳中和、碳达峰”知识的知晓情况，某校团委随机对该校九年级部分学生进行了问卷调查，调查结果共分成四个类别：A表示“从未听说过”，B表示“不太了解”，C表示“比较了解”，D表示“非常了解”．根据调查统计结果，绘制成两种不完整的统计图，请结合统计图，回答下列问题：
1. （1）参加这次调查的学生总人数为▲ 人；将条形统计图补充完整；
2. （2）扇形统计图中，B部分扇形所对应的圆心角是；
3. （3）若该中学共有学生2000人，请根据上述调查结果，估计该中学学生中对“碳中和、碳达峰”知识达到“比较了解”和“非常了解”程度的总人数；
4. （4）在D类的学生中，有2名男生和2名女生，现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员，请利用画树状图或列表的方法，求所抽取的2名学生恰好是1名男生和1名女生的概率．
答案解析收藏纠错 + 选题

28. (2023·曾都模拟) 数字正在改变人们的生活．某校开展了一次数字科技知识测试，并从中随机抽取部分学生的测试成绩进行统计，绘制了如图所示的不完整的统计表和统计图（测试结果共分四个等级：A．优秀；B．良好；C．及格；D．不及格）．

测试等级	A优秀	B良好	C及格	D不及格
人数	20	60		140
百分比	5%		45%	m

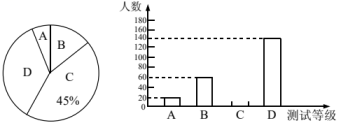
根据以上信息，回答下列问题：

（1）本次参与调查的学生人数为，m的值为；
（2）扇形统计图中“B良好”对应的圆心角的度数为 ▲ ，并补全条形统计图；
（3）本次测试前4名学生中，七、八年级各1人，九年级2人，学校准备从这4名学生中，随机抽取两人报名参加全市创意编程大赛，请用画树状图或列表的方法，求恰好抽到两名九年级学生的概率．

答案解析收藏纠错 + 选题

六、新定义统计概率应用

29. (2024·从江模拟) 如果一个三位数中任意两个相邻数字之差的绝对值不超过1，则称该三位数为“平稳数”．用 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 这三个数字随机组成一个无重复数字的三位数，恰好是“平稳数”的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

30. (2023·黄石) 健康医疗大数据蕴藏了丰富的居民健康状况、卫生服务利用等海量信息，是人民健康保障的数据金矿和证据源泉 $\text{[math]}$ 目前，体质健康测试已成为中学生的必测项目之一 $\text{[math]}$ 某校某班学生针对该班体质健康测试数据开展调查活动，先收集本班学生八年级的 $\text{[math]}$ 体质健康标准登记表 $\text{[math]}$ ，再算出每位学生的最后得分，最后得分记为 $\text{[math]}$ ，得到下表：

成绩	频数	频率
不及格 $\text{[math]}$	$\text{[math]}$
及格 $\text{[math]}$		$\text{[math]}$
良好 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$
优秀 $\text{[math]}$	$\text{[math]}$

（1）请求出该班总人数；
（2）该班有三名学生的最后得分分别是 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将他们的成绩随机填入表格，求恰好得到的表格是的概率；
（3）设该班学生的最后得分落在不及格，及格，良好，优秀范围内的平均分分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，请求出该班全体学生最后得分的平均分，并估计该校八年级学生体质健康状况．

答案解析收藏纠错 + 选题

31. (2023·盘锦) 某校为了解学生平均每天阅读时长情况，随机抽取了部分学生进行抽样调查，将调查结果整理后绘制了以下不完整的统计图表 $\text{[math]}$ 如图所示 $\text{[math]}$

学生平均每天阅读时长情况统计表

平均每天阅读时长 $\text{[math]}$	人数
$\text{[math]}$	20
$\text{[math]}$	a
$\text{[math]}$	25
$\text{[math]}$	15
$\text{[math]}$	10

根据以上提供的信息，解答下列问题：

（1）本次调查共抽取了名学生，统计表中 $\text{[math]}$ .
（2）求扇形统计图中学生平均每天阅读时长为“ $\text{[math]}$ ”所对应的圆心角度数.
（3）若全校共有1400名学生，请估计平均每天阅读时长为“ $\text{[math]}$ ”的学生人数.
（4）该校某同学从《朝花夕拾》《红岩》《骆驼祥子》《西游记》四本书中选择两本进行阅读，这四本书分别用相同的卡片A ， B ， C ， D标记，先随机抽取一张卡片后不放回，再随机抽取一张卡片，请用列表法或画树状图法，求该同学恰好抽到《朝花夕拾》和《西游记》的概率.

答案解析收藏纠错 + 选题

32. (2021·徐州) 如图，是一个竖直放置的钉板，其中，黑色圆面表示钉板上的钉子， $\text{[math]}$ 分别表示相邻两颗钉子之间的空隙，这些空隙大小均相等，从入口 $\text{[math]}$ 处投放一个直径略小于两颗钉子之间空隙的圆球，圆球下落过程中，总是碰到空隙正下方的钉子，且沿该钉子左右两个相邻空隙继续下落的机会相等，直至圆球落入下面的某个槽内.用画树状图的方法，求圆球落入③号槽内的概率.

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

备战2024年中考数学细点逐一突破真题训练第16章概率统计初...

副标题：

*注意事项：

备战2024年中考数学细点逐一突破真题训练第16章概率统计初...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

28	62	54	39	32	47	68	27	65	43
52	59	67	59	45	42	79	51	54	25
82	18	39	32	64	74	49	37	39	52

分组	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
频数	2	$\text{[math]}$	7	$\text{[math]}$	5	3	2

成绩x(分)	60≤x<70	70≤x<80	80≤x<90	90≤x<100
七年级	1	5	a	2
八年级	0	4	5	1

	平均数(分)	中位数(分)	众数(分)	方差(分²)
七年级	80	c	72	64.4
八年级	b	80	d	37.6

年级	七年级	八年级
平均数	$\text{[math]}$	$\text{[math]}$
中位数	$\text{[math]}$	$\text{[math]}$
方差	$\text{[math]}$	$\text{[math]}$

马匹等级	下等马	中等马	上等马
齐王	2	4	6
田忌	1	3	5

28	62	54	39	32	47	68	27	65	43
52	59	67	59	45	42	79	51	54	25
82	18	39	32	64	74	49	37	39	52

28	62	54	39	32	47	68	27	65	43
52	59	67	59	45	42	79	51	54	25
82	18	39	32	64	74	49	37	39	52