
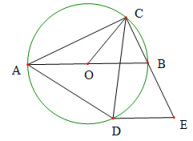
①点D是定点;
②AC•BC的最大值为50;
③D为△ABE的外心;
④CA+CB的最大值为 .
其中正确的有( )


如何确定拍照打卡板 | ||
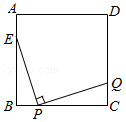
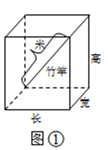
素材一 | 设计师小聪为某商场设计拍照打卡板(如图1),图2为其平面设计图.该打卡板是轴对称图形,由长方形DEFG和等腰三角形ABC组成,且点B , F , G , C四点共线.其中,点A到BC的距离为1.2米, |
|
素材二 | 因考虑牢固耐用,小聪打算选用甲、乙两种材料分别制作长方形DEFG与等腰三角形ABC(两种图形无缝隙拼接),且甲材料的单价为85元/平方米,乙材料的单价为100元/平方米. |
|
问题解决 | ||
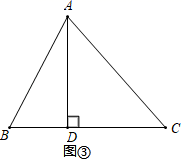
任务一 | 推理最大高度 | 小聪说:“如果我设计的方案中CB长与C , D两点间的距离相等,那么最高点B到地面的距离就是线段DG长”,他的说法对吗?请判断并说明理由. |
任务二 | 探究等腰三角形ABC面积 | 假设CG长度为x米,等腰三角形ABC的面积为S , 求S关于x的函数表达式. |
任务三 | 确定拍照打卡板 | 小聪发现他设计的方案中,制作拍照打卡板的总费用不超过180元,请你确定CG长度的最大值. |
配方法是数学中一种很重要的恒等变形方法,我们已经学习了用配方法解一元二次方程,并在此基础上得出了一元二次方程的求根公式.其实配方法还有很多重要的应用.例如我们可以用配方法求代数式的最值及取得最值的条件,如下面的例子:
例:求多项式的最小值
解:
,
多项式的最小值为−7,此时,
.
仿照上面的方法,解决下面的问题:

素材一 | 如图,在Rt |
|
素材二 | 如图,在Rt△ABC中, |
|
素材三 | 如图,矩形ABCD是某实验室侧截面示意图,现需要在室内安装一块长1米的遮光板EF,且EF//AB,点 |
|
任务一 | 若素材一中的AB=4,求CD的最大值. | |
任务二 | 若素材二中的CD=6,求AB的最小值. | |
任务三 | 若任务二中的∠ACB=90°改成∠ACB=60°,其余条件不变,请直接写出AB的最小值. |
|
任务四 | 若任务二中的∠ACB=90°,CD=6改成∠ACB=α,CD=m,请直接出AB的最小值. | |
任务五 | 当素材三中的实验室“可利用比”最高,求此时BM+BN的值 |
(类比探究)为了解决这个实际问题,我们首先探究下面的数学问题.
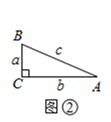
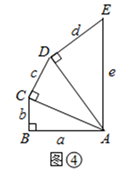
探究:如图②,在 中,
.若
,
,
,则
与
之有什么数量关系?
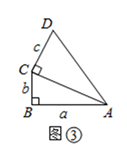
解:在 中,
,
,即
.
,
,
,
,
.
.
,
,
均大于
,
与
之间的数量关系是
.
解:
,
,
,
.
,
,
,
,
,
.
将上面三式相加得, ,
.
.
.
,
,
,
均大于
,
与
之间有这样的数量关系:
.
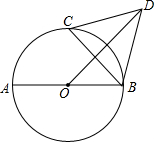
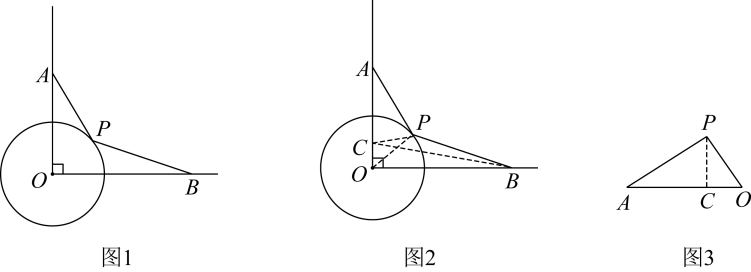
【问题呈现】如图1,∠AOB=90°, OA=4,OB=5,点P在半径为2的⊙O上,求的最小值.
【问题解决】小明是这样做的:如图2,在OA上取一点C使得OC=1,这样可得 , 又因为∠COP=∠POA,所以可得△COP ∽△POA,所以
, 得
所以
.
又因为 , 所以
最小值为 ▲ .
【思路点拨】小明通过构造相似形(图3),将转化成CP,再利用“两点之间线段”最短”求出CP+ BP的最小值.
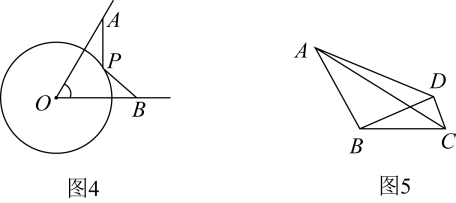
【尝试应用】如图4,∠AOB=60°, OA=10,OB=9,点P是半径为6的⊙O上一动点,求的最小值.
【能力提升】如图5,∠ABC=120°, BA= BC=8,点D为平面内一点且BD= 3CD,连接AD,则△ABD面积的最大值为 ▲ .
|
初步探索 |
素材1:
如图①,连接对应点 |
素材2:
如图②,以 |
|
问题解决 |
(1)(ⅰ)请证明素材1所发现的结论. (ⅱ)如图2,过点
|
|
|
深入研究 |
(2)在 (ⅰ)如图③,当边 (ⅱ)若一时边 (3)在(2)的条件下,如图⑤,在旋转过程中,直线 |
|
|
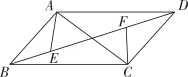
数学活动课上,老师提出如下问题: 如图①,在四边形ABCD中,AB⊥BC,DC⊥BC,AB=2,DC=4,BC=8,点P为BC边上的动点,求当BP的值是多少时,AP+DP有最小值,最小值是多少. 小丽和小明对老师提出的问题进行了合作探究: 小丽:设BP=x,则CP=8﹣x,根据勾股定理,可得AP+DP= 小明:利用轴对称作图,如图②,作点A关于直线BC的对称点A′,连接A′D,与BC交于点P,根据两点之间线段最短,将求AP+DP的最小值转化为求线段A'D的长. 由△A′BP∽△DCP,得 所以BP= 过点A′作A′H⊥DC,交DC的延长线于点H,再由勾股定理,可得A′D= 所以当BP= |
任务: