
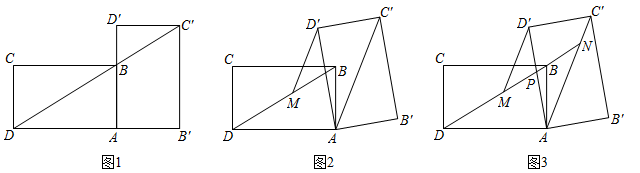
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.

① ② ③
如图①所示,连接BE,DE.求证:BE=DE;
如图②所示,F是DE延长线上一点,EF交AB于点G,FB⊥BE,判断△FBG的形状,并说明理由;
如图③所示,F是DE延长线上一点,EF交AB于点G,FB⊥BE,BE=BF,求证:GE=(-1)DE.
当时,将
绕点C旋转,使
三点恰好在同一直线上,求
的长.

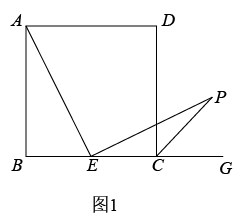
如图1,在正方形ABCD中,点P在边AB的延长线上,连结PD , 过点D作DM⊥PD , 交BC的延长线于点M . 求证:△DAP≌△DCM .
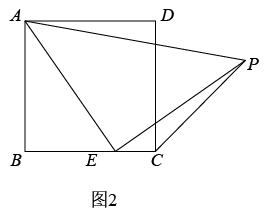
如图2,在Rt△ABC中,∠ABC=90°,点D在边AB上,过点D作DQ⊥AB , 交AC于点Q , 点P在边AB的延长线上,连结PQ , 过点Q作QM⊥PQ , 交射线BC于点M . 已知BC=8,AC=10,AD=2DB , 求的值.
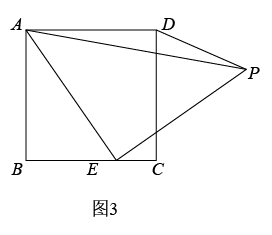
如图3,在Rt△ABC中,∠BAC=90°,点P在边AB的延长线上,点Q在边AC上(不与点A , C重合),连结PQ , 以Q为顶点作∠PQM=∠PBC , ∠PQM的边QM交射线BC于点M . 若AC=mAB , CQ=nAC(m , n是常数),求的值(用含m , n的代数式表示).
人教版八年级下册数学教材第63页“实验与探究”问题1如下:如图,正方形的对角线相交于点
, 点
又是正方形
的一个顶点,而且这两个正方形的边长相等,无论正方形
绕点
怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的
. 想一想,这是为什么?(此问题不需要作答)
九年级数学兴趣小组对上面的问题又进行了拓展探究、内容如下:正方形的对角线相交于点
, 点
落在线段
上,
为常数).

如图1,将的直角顶点
与点
重合,两直角边分别与边
,
相交于点
,
.
①填空: ▲ ;
②求证: . (提示:借鉴解决【问题背景】的思路和方法,可直接证明
;也可过点
分别作
,
的垂线构造全等三角形证明.请选择其中一种方法解答问题②.
如图2,将图1中的沿
方向平移,判断
与
的数量关系(用含
的式子表示),并说明理由.
如图3,点在边
上,
, 延长
交边
于点
, 若
, 求
的值.
2.如图,在正方形ABCD中, 证明:设CE与DF交于点O, ∵四边形ABCD是正方形, ∴ ∴ ∵ ∴ ∴ ∴ ∴ ∴
|
某数学兴趣小组在完成了以上解答后,决定对该问题进一步探究





①求A,B两点的坐标;
②求ME的长.
如图1,在正方形中,对角线
相交于点O.在线段
上任取一点P(端点除外),连接
.
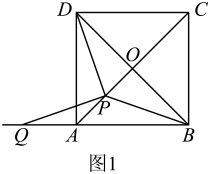
①求证:;
②将线段绕点P逆时针旋转,使点D落在
的延长线上的点Q处.当点P在线段
上的位置发生变化时,
的大小是否发生变化?请说明理由;
③探究与
的数量关系,并说明理由.
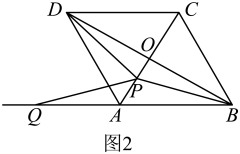
如图2,将正方形换成菱形
, 且
, 其他条件不变.试探究
与
的数量关系,并说明理由.
拓展应用:
当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图1中的是黄金三角形.如图2,在菱形
中,
,
. 求这个菱形较长对角线的长.

当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图1中的是黄金三角形.如图2,在菱形
中,
,
. 求这个菱形较长对角线的长.
