2024-2025学年浙教版数学九上第1章二次函数三阶单...

更新时间：2024-07-24 浏览次数：49 类型：单元试卷

一、选择题（本题有10小题，每小题3分，共30分）

1. (2024·江汉模拟) 已知点A（x₁ ， y₁）在抛物线y₁＝nx²﹣2nx+n上，点B（x₂ ， y₂）在直线y₂＝﹣nx+n，当n＞0时，下列判断正确的是（　　）

A . 当x₁＝x₂＜1时，y₁＜y₂ B . 当x₁＝x₂＞1时，y₁＜y₂ C . 当y₁＝y₂＞n时，x₁＞x₂ D . 当y₁＝y₂＜n时，x₁＞x₂

答案解析收藏纠错 + 选题
2. (2024·拱墅模拟) 定义符号min{a，b}的含义为：当a≥b时min{a，b}＝b；当a＜b时min{a，b}＝a．如min{1，﹣3}＝﹣3，min{﹣4，﹣2}＝﹣4．则min（﹣x²+3，﹣2x}的最大值是（）

A . 3 B . 2 C . 1 D . 0

答案解析收藏纠错 + 选题
3. (2024·南海模拟) 据科学计算，运载“神十八”的“长征二号” $\text{[math]}$ 火箭，在点火第一秒钟通过的路程为 $\text{[math]}$ ，第二秒时共通过了 $\text{[math]}$ 的路程，第三秒时共通过了 $\text{[math]}$ 的路程，在这一过程中路程与时间成二次函数关系，在达到离地面 $\text{[math]}$ 的高度时，火箭程序拐弯，则这一过程需要的时间大约是（）．

A . 10秒钟 B . 13秒钟 C . 15秒钟 D . 20秒钟

答案解析收藏纠错 + 选题
4. (2020九下·金溪月考) 反比例函数 $\text{[math]}$ 的图象如图所示，则二次函数y＝2kx²﹣4x+k²的图象大致是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024·柳州三模) 在平面直角坐标系中，二次函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象与x轴的一个交点的横坐标为 $\text{[math]}$ ，则另一个交点的横坐标为（）

A . 5 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·仪陇模拟) 已知点 $\text{[math]}$ ， $\text{[math]}$ 都在抛物线 $\text{[math]}$ 上，若当 $\text{[math]}$ 时，都有 $\text{[math]}$ ，则实数k的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·台州) 抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，若 $\text{[math]}$ ，则直线 $\text{[math]}$ 一定经过（）．

A . 第一、二象限 B . 第二、三象限 C . 第三、四象限 D . 第一、四象限

答案解析收藏纠错 + 选题
8. (2024·湖南模拟) 如图，四边形 $\text{[math]}$ 为菱形， $\text{[math]}$ 为 $\text{[math]}$ 上一点， $\text{[math]}$ 的垂直平分线交 $\text{[math]}$ 于点F ，若 $\text{[math]}$ ，记 $\text{[math]}$ 的面积最大值为S ，周长最小值为l ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 关于一元二次方程 $\text{[math]}$ 有以下命题：①若a+b+c=0，则( $\text{[math]}$ ≥0；②若方程( $\text{[math]}$ 的两根为-1和2，则2a+c=0；③若方程( $\text{[math]}$ 有两个不相等的实数根，则方程 $\text{[math]}$ =0必有两个不相等的实数根；④若方程 $\text{[math]}$ 有两个相等的实数根，则 $\text{[math]}$ 无实数根.其中真命题是（）

A . ①② B . ①②③ C . ②③④ D . ①③④

答案解析收藏纠错 + 选题
10. (2024九下·南山开学考) 如图，是二次函数 $\text{[math]}$ 图象的一部分，图象过点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④若 $\text{[math]}$ ， $\text{[math]}$ 为函数图象上的两点，则 $\text{[math]}$ ．其中正确的结论有　　

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2024·武威) 如图1为一汽车停车棚，其棚顶的横截面可以看作是抛物线的一部分，如图2是棚顶的竖直高度y(单位：m)与距离停车棚支柱AO的水平距离x(单位：m)近似满足函数关系 $\text{[math]}$ 的图象，点 $\text{[math]}$ 在图象上.若一辆箱式货车需在停车棚下避雨，货车截面看作长 $\text{[math]}$ ，高 $\text{[math]}$ 的矩形，则可判定货车完全停到车棚内（填“能”或“不能”）.

答案解析收藏纠错 + 选题
12. (2020九上·高淳期中) 如图，平面直角坐标系中，桥孔抛物线对应的二次函数关系式是y＝﹣ $\text{[math]}$ x² ，桥下的水面宽AB为6m，当水位上涨2m时，水面宽CD为m（结果保留根号）.

答案解析收藏纠错 + 选题
13. (2024八下·百色期中) 从地面竖直向上抛出一个小球，若小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系满足 $\text{[math]}$ ，则小球从抛出到落地共用时s．

答案解析收藏纠错 + 选题
14. (2024·义乌模拟) 如图，抛物线 $\text{[math]}$ 的图象与x轴交于点A ，与y轴交于点B ，且 $\text{[math]}$ ．
1. （1） $\text{[math]}$ ．
2. （2）已知点P为该抛物线上一点且设其横坐标为 $\text{[math]}$ ，记该抛物线在点B与点P之间（包含点B和点P）这部分图象的最高点和最低点到x轴的距离分别为 $\text{[math]}$ ．若 $\text{[math]}$ ，则t的取值范围为．
答案解析收藏纠错 + 选题
15. (2023九上·龙湾期中) 图1是一个瓷碗，图 2 是其截面图，碗体 DEC 呈抛物线状（碗体厚度不计），碗口宽CD＝12cm，此时面汤最大深度EG＝8cm．
1. （1）当面汤的深度ET为4cm时，汤面的直径PQ长为；
2. （2）如图3，把瓷碗绕点B缓缓倾斜倒出部分面汤，当∠ABM=45°时停止，此时碗中液面宽度CH=．
答案解析收藏纠错 + 选题
16. (2023·惠山模拟) 抛物线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 是常数且 $\text{[math]}$ ， $\text{[math]}$ ）经过点 $\text{[math]}$ ．下列四个结论：①该抛物线一定经过 $\text{[math]}$ ；② $\text{[math]}$ ；③点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线上，且 $\text{[math]}$ ，则 $\text{[math]}$ ④若 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两个根，其中 $\text{[math]}$ ，则 $\text{[math]}$ ．其中正确的结论是（填写序号）．

答案解析收藏纠错 + 选题

三、解答题（本题共8小题，第17题9分，第18题9分，第19题6分，第20题9分，第21题9分，第22题4分，第23题10分，第24题10分，共66分）

17. (2024·温岭二模) 已知，关于 $\text{[math]}$ 的二次函数 $\text{[math]}$ ．
1. （1）若函数 $\text{[math]}$ 经过点 $\text{[math]}$ ，求拋物线的对称轴．
2. （2）若点P(t-2，p)，Q(t+3，q)均在抛物钱y=2x²-4tx-3上，则pq(填">"，“<"或"=”).
3. （3）记 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 始终成立，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
18. (2024·新乐模拟) 已知二次函数的图象L过点 $\text{[math]}$ ，顶点坐标为 $\text{[math]}$ ．
1. （1）求这个二次函数的表达式；
2. （2） L与x轴相交于A ， B两点（点A在点B左侧），求A ， B两点坐标；
3. （3）将L向上平移个 $\text{[math]}$ 单位长度，与x轴相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，若点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，求k的取值范围．
答案解析收藏纠错 + 选题
19. (2024·官渡模拟) 已知二次函数 $\text{[math]}$ （ $\text{[math]}$ 为常数且 $\text{[math]}$ ）的顶点在 $\text{[math]}$ 轴上方，且到 $\text{[math]}$ 轴的距离为4．
1. （1）求二次函数的解析式；
2. （2）将二次函数 $\text{[math]}$ 的图象记为 $\text{[math]}$ ，将 $\text{[math]}$ 关于原点对称的图象记为 $\text{[math]}$ 与 $\text{[math]}$ 合起来得到的图象记为 $\text{[math]}$ ，完成以下问题：
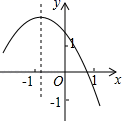
  ①在网格中画出函数 $\text{[math]}$ 的图象；
  ②若对于函数 $\text{[math]}$ 上的两点 $\text{[math]}$ ，当 $\text{[math]}$ 时，总有 $\text{[math]}$ ，求出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
20. (2024·利川模拟) 某商品每件进价25元，在试销阶段该商品的日销售量y（件）与每件商品的日销售价x（元）之间的关系如图中的折线ABC所示（物价局规定，该商品每件的销售价不得低于进价且不得高于50元）．
1. （1）直接写出y与x的函数关系式；
2. （2）若日销售单价x（元）为整数，则当日销售单价x（元）为多少时，该商品每天的销售利润最大？最大利润是多少；
3. （3）若该商品每天的销售利润不低于1200元，求销售单价x的取值范围．
答案解析收藏纠错 + 选题
21. (2024·罗湖模拟) 【项目式学习】
项目主题：如何拟定运动员拍照记录的方案？
项目背景：
1. （1）任务一：确定滑道的形状
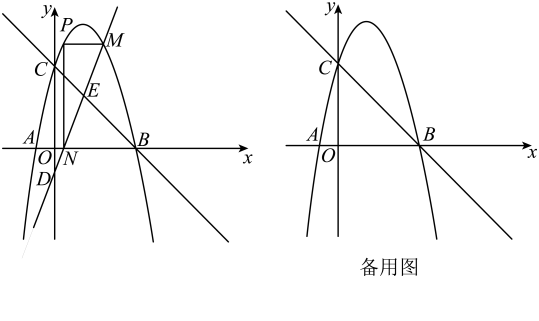
  图1是单板滑雪运动员从大跳台滑雪场地滑出的场景，图2是跳台滑雪场地的横截面示意图．AC垂直于水平底面BC，点D到A之间的滑道呈抛物线型，已知 $\text{[math]}$ m， $\text{[math]}$ m，且点B处于跳台滑道的最低处，在图2中建立适当的平面直角坐标系，求滑道所在抛物线的函数表达式．
2. （2）任务二：确定运动员达到最高点的位置
  如图3，某运动员从点A滑出后的路径满足以下条件：
  ①运动员滑出路径与D、A之间的抛物线形状相同，
  ②该运动员在底面BC上方竖直距离9.75m处达到最高点P
  ③落点Q在底面BC下方竖直距离2.25m．
  在同一平面直角坐标系中，求运动员到达最高处时与点A的水平距离．
3. （3）任务三：确定拍摄俯角 $\text{[math]}$
  高速摄像机能高度还原运动员的精彩瞬间，如图4，有一台摄像机M进行跟踪拍摄：
  ①它与点B位于同一高度，且与点B距离25.5m；
  ②运动过程需在摄像头视角范围内才能记录，记摄像头的俯角为 $\text{[math]}$ ；
  ③在平面直角坐标系中，设射线MN的解析式为 $\text{[math]}$ ，其比例系数k和俯角 $\text{[math]}$ 的函数关系如图5所示．
  若要求运动员的落点Q必须在摄像机M的视角范围内，则俯角 $\text{[math]}$ 至少多少度（精确到个位）？
答案解析收藏纠错 + 选题

22. (2024·义乌模拟)

草莓种植大棚的设计
生活背景	草莓种植大棚是一种具有保温性能的框架结构．如图示，一般使用钢结构作为骨架，上面覆上一层或多层塑料膜，这样就形成了一个温室空间．大棚的设计要保证通风性且利于采光．
建立模型	$\text{[math]}$ 如图1，已知某草莓园的种植大棚横截面可以看作抛物线 $\text{[math]}$ ，其中点P为抛物线的顶点，大棚高 $\text{[math]}$ ，宽 $\text{[math]}$ ．现以点O为坐标原点， $\text{[math]}$ 所在直线为x轴，过点O且垂直于 $\text{[math]}$ 的直线为y轴建立平面直角坐标系．求此抛物线的解析式．图1
解决问题	$\text{[math]}$ 如图2，为方便进出，在大棚横截面中间开了两扇正方形的门，其中 $\text{[math]}$ ．求门高 $\text{[math]}$ 的值． $\text{[math]}$ 若在某一时刻，太阳光线（假设太阳光线为平行线）透过A点恰好照射到N点，此时大棚横截面在地面上的阴影为线段 $\text{[math]}$ ，求此时 $\text{[math]}$ 的长．图2

答案解析收藏纠错 + 选题

23. (2023·济宁) 如图，直线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，对称轴为 $\text{[math]}$ 的抛物线经过 $\text{[math]}$ 两点，交 $\text{[math]}$ 轴负半轴于点 $\text{[math]}$ ． $\text{[math]}$ 为抛物线上一动点，点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴的平行线交抛物线于另一点 $\text{[math]}$ ，作 $\text{[math]}$ 轴的垂线 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，直线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．
1. （1）求抛物线的解析式；
2. （2）若 $\text{[math]}$ ，当 $\text{[math]}$ 为何值时，四边形 $\text{[math]}$ 是平行四边形？
3. （3）若 $\text{[math]}$ ，设直线 $\text{[math]}$ 交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，是否存在这样的 $\text{[math]}$ 值，使 $\text{[math]}$ ？若存在，求出此时 $\text{[math]}$ 的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
24. (2024·威远模拟) 如图，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 、 $\text{[math]}$ 两点， $\text{[math]}$ 为抛物线上第一象限内的一个动点．
1. （1）求抛物线所对应的函数表达式；
2. （2）当 $\text{[math]}$ 的面积最大时，求点 $\text{[math]}$ 的坐标；
3. （3）过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ ，若存在，求点 $\text{[math]}$ 的横坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题