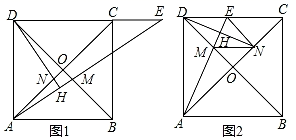
⑴EF= OE;
⑵S四边形OEBF:S正方形ABCD=1:4;
⑶BE+BF= OA;
⑷在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;
⑸OG•BD=AE2+CF2 .

① ;②
;③
;④不等式
的取值范围是
.其中正确的结论有( )





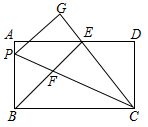
①BP=BF;②若点E是AD的中点,那么△AEB≌△DEC;③当AD=25,且AE<DE时,则DE=16;④在③的条件下,可得sin∠PCB= ;⑤当BP=9时,BE•EF=108.


①点O与 的距离为4;②
;③
;④
.



①求证:CA=CF;
②若 的半径为3,BF=2,求AC的长.

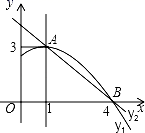
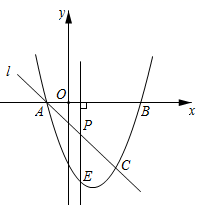
①求抛物线L的解析式;
②若直线PC交抛物线L于点E(x1 , y1)、F(x2 , y2),交y轴于点Q,平面内一点H坐标为H(4 ,2),记d=|x1﹣x2|,当点P在⊙B上运动时,求(
)2的取值范围.
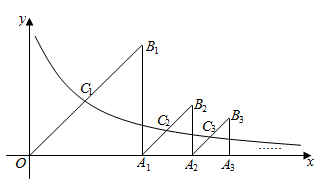
①求C1关于点R(1,0)的对称函数图象C2的函数解析式;
②若两抛物线与y轴分别交于A、B两点,当AB=16时,求a的值;

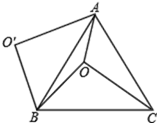
如图1,在 中,
为
上一点,
.求证:
.
如图2,在 中,
为
上一点,
为
延长线上一点,
,若
,
,求
的长.
如图3,在菱形 中,
是
上一点,
是
内一点,
,
,
,
,
,求菱形
的边长.
①点P在运动过程中,线段PD的长度是否存在最大值?若存在,请求出点D的坐标;若不存在,请说明理由;
②以P、D、C为顶点的三角形与△COA相似时,求出点P的坐标.
① ;②
;③
①求 的值;
②如图2,若该抛物线经过点(0,6),∠BAD的平分线交BD于点P,点M为射线AB上一点.连接直线PM交射线AD于点N,求 的值.

求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式,求解二元一次方程组,把它转化为一元一次方程来解;类似的,三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为 ,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.