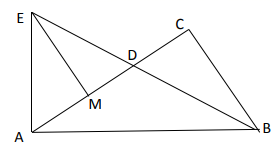
①若E是AB的中点,求△OEF的面积.
②连结DE,当△DEF是以DE为腰的等腰三角形时,求CF的长.
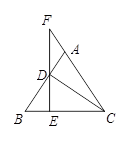



①若∠MON=50°,则∠GOH= ▲ ;
②若PO=5,连接GH,请说明当∠MON为多少度时,GH=10;



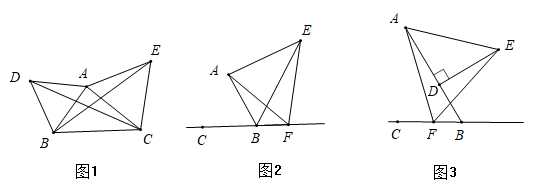
(小试牛刀)把两个全等的直角三角形△ABC和△DAE如图1放置,其三边长分别为a , b , c . 显然,∠DAB=∠B=90°,AC⊥DE . 请用a , b , c分别表示出梯形ABCD , 四边形AECD , △EBC的面积:
S梯形ABCD=,
S△EBC=,
S四边形AECD=,
再探究这三个图形面积之间的关系,它们满足的关系式为,化简后,可得到勾股定理.
(知识运用)
如图2,河道上A , B两点(看作直线上的两点)相距200米,C , D为两个菜园(看作两个点),AD⊥AB , BC⊥AB , 垂足分别为A , B , AD=80米,BC=70米,现在菜农要在AB上确定一个抽水点P , 使得抽水点P到两个菜园C , D的距离和最短,则该最短距离为米.
(知识迁移)
借助上面的思考过程,请直接写出当0<x<15时,代数式 的最小值=.

如图2,已知 ,点F在直线BC上,以AF为边作等边三角形AEF , 连接BE , 求证:
;
在(2)的条件下,当点F运动到射线BC上时,过点E作 于点D , 请直接写出线段AB , BF与BD之间存在的数量关系.
①如图1,∠BCA=90°,∠α=90°,写出BE , EF , AF间的等量关系:.
②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立?写出∠α与∠BCA的数量关系 .

①当ΔACE的面积为12时,求t的值;
②在点E运动过程中,是否存在t的值,使ΔACE为直角三角形?若存在,请求出t的值;若不存在,请说明理由.

如图③,∠CBO= ∠DBC,∠BCO=
∠ECB,∠A=α,求∠BOC的度数(用α表示),并说明理由.