 问题情境:如图,将一个圆锥的侧面展开后可得到一个圆心角为
问题情境:如图,将一个圆锥的侧面展开后可得到一个圆心角为 , 半径为l的扇形
, 圆锥底面是一个半径为r的圆.母线
在展开图上对应的半径
经过
的中点.
请阅读下列材料,并完成相应的任务.
在《阿基米德全集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的关于圆的一些问题,其中有这样一个问题:如图1,
证明:如图2,在 ∵ ∴ ∵ ∴ ∴ …… |
任务:



①半余三角形一定是钝角三角形;
②直角三角形不可能是半余三角形;
③任何直角三角形都能分割成两个半余三角形.


①试说明△ABK是等腰三角形.
②当点G为AK中点时,求a的值.
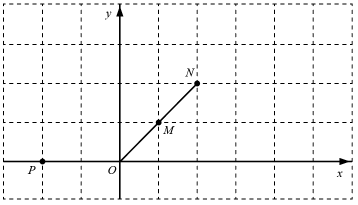
①在图中画出点;
②连接交线段
于点
求证:
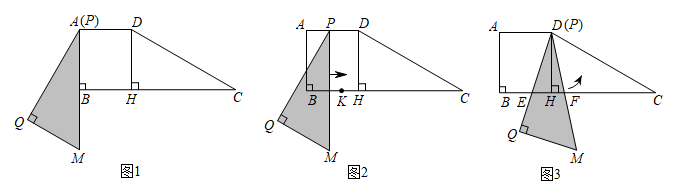
①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且 .若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3.在△PQM旋转过程中,设PQ , PM分别交BC于点E , F , 若BE=d , 直接写出CF的长(用含d的式子表示).