
 B .
B .  C .
C . 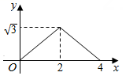 D .
D . 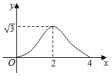
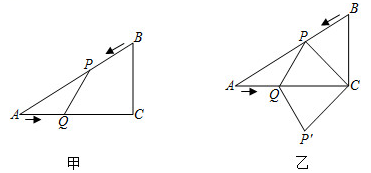
.
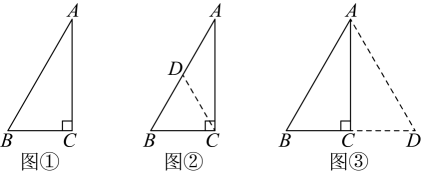
【证明】如图 , 在
中,
,
. 求证:
.
方法一:如图 , 作斜边
上的中线
, 则
.
,
.
是 ▲ 三角形.
.
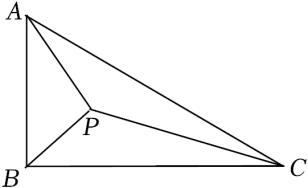
方法二:如图 , 作点
关于
的对称点
, 连接
.
,
,
.
是等边三角形.
▲ .
.
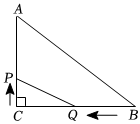
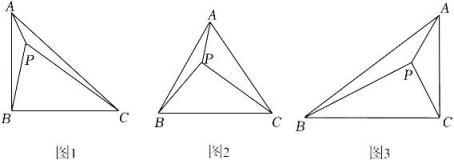
①若 , 点
到边
的距离为 ▲ .
②若 , 求点
到边
的距离.
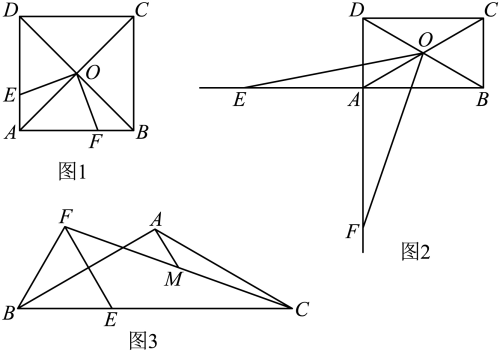
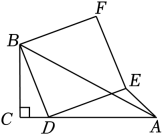
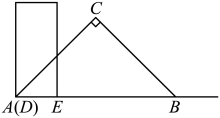
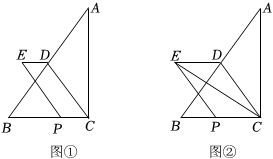
①如图1,当顶点D在边AC上时,请直接写出∠EAB与∠CBA的数量关系是 ▲ . 线段BE与线段CF的数量关系是 ▲ ;
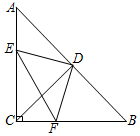
②如图2,当顶点D在边AB上时,(1)中线段BE与线段CF的数量关系是否仍然成立?若成立,请给予证明,若不成立,请说明理由;
学生经过讨论,探究出以下解决问题的思路,仅供大家参考:
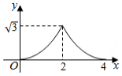
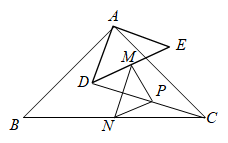
思路一:作等腰△ABC底边上的高CM , 并取BE的中点N , 再利用三角形全等或相似有关知识来解决问题;
思路二:取DE的中点G , 连接AG , CG , 并把绕点C逆时针旋转90°,再利用旋转性质、三角形全等或相似有关知识来解快问题.