备考2024年中考数学重难创新题4 与三角形有关的证明与计...

更新时间：2024-05-20 浏览次数：49 类型：二轮复习

一、新考法-跨学科

1. (2022九上·温州开学考) 如图为一块光学直角棱镜，其截面为直角三角形 $\text{[math]}$ ， $\text{[math]}$ 所在的面为不透光的磨砂面， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 现将一束单色光从 $\text{[math]}$ 边上的 $\text{[math]}$ 点入射，折射后到达 $\text{[math]}$ 边上的 $\text{[math]}$ 点，恰有 $\text{[math]}$ ，再经过反射后 $\text{[math]}$ 即 $\text{[math]}$ ，从 $\text{[math]}$ 点垂直于 $\text{[math]}$ 射出，则光线在棱镜内部经过的路径 $\text{[math]}$ 的总长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·福田模拟) 如图，⊙O的半径为r，交×轴正半轴于点A，直线l垂直平分OA交⊙O于点P，PB⊥y轴于点B．今假设在点O，A处，分别有一质量为m₁ ， m₂的天体(m₁>m₂)；天体物理中把与O，A处于同一平面，坐标为（ $\text{[math]}$ ， $\text{[math]}$ ）的点称为[O，A]系统的拉格朗日4号点，记为L₄ (若把卫星发射到L₄的位置，则卫星会处于相对静止的稳状态)．以下说法中错误的是（）

A . △AOP是等边三角形 B . L₄在线段BP上 C . ∠OL₄A>60° D . 若m₁恒定，则m₂越小，L₄离点P越近

答案解析收藏纠错 + 选题
3. (2024八下·大化月考) 小明在物理课上学习了发声物体的振动实验后，对其作了进一步的探究：在一个支架的横杆点 $\text{[math]}$ 处用一根细绳悬挂一个小球 $\text{[math]}$ ，小球 $\text{[math]}$ 可以自由摆动，如图， $\text{[math]}$ 表示小球静止时的位置．当小明用发声物体靠近小球时，小球从 $\text{[math]}$ 摆到 $\text{[math]}$ 位置，此时过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，当小球摆到 $\text{[math]}$ 位置时， $\text{[math]}$ 与 $\text{[math]}$ 恰好垂直（图中的 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一平面上），过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，测得 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）试说明： $\text{[math]}$ ；
2. （2）求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
4. (2022七下·义乌期中) 光线反射是一种常见的物理现象，在生活中有广泛地应用.例如提词器可以帮助演讲者在看演讲词的同时也能面对摄像机，自行车尾部的反光镜等就是应用了光的反射原理.
1. （1）自行车尾部的反光镜在车灯照射下，能把光线按原来的方向返回（如图②），a表示入射光线，b表示反射光线， $\text{[math]}$ .平面镜AB与BC的夹角∠ABC=α，则α=.
2. （2）如图③，若α=108°，设平面镜CD与BC的夹角∠BCD=β（90°＜β＜180°），入射光线a与平面镜AB的夹角为x（0°＜x＜90°），已知入射光线a从平面镜AB开始反射，经过2或3次反射，当反射光线b与入射光线a平行时，请直接写出β=.（可用含x的代数式表示）
答案解析收藏纠错 + 选题
5. (2023八上·衡阳期中) 【学科融合】如图1，在反射现象中，反射光线，入射光线和法线都在同一个平面内；反射光线和入射光线分别位于法线两侧；反射角r等于入射角i．这就是光的反射定律
图1 图2
【同题解决】如图2．小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜，手电简的灯泡在点G处，手电简的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处，点F到地面的高度 $\text{[math]}$ ，点A、点C到平面镜B点的距离相等．图中点A，B，C，D在同一条直线上．求灯泡到地面的高度 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
6. (2023·天门模拟) 在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，推动“连杆”带动磨盘转动，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”.
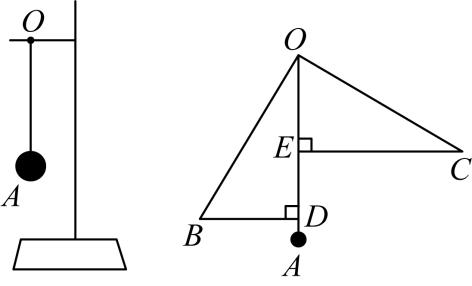
小明受此启发设计了一个“双连杆机构”，设计图如图1，两个固定长度的“连杆” $\text{[math]}$ ， $\text{[math]}$ 的连接点P在 $\text{[math]}$ 上，当点P在 $\text{[math]}$ 上转动时，带动点A，B分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上滑动， $\text{[math]}$ .当 $\text{[math]}$ 与 $\text{[math]}$ 相切时，点B恰好落在 $\text{[math]}$ 上，如图2.请仅就图2的情形解答下列问题.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 的半径为3， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
7. (2024九下·石家庄开学考) 粒子加速器是当今高能物理学中研究有关宇宙的基本问题的重要工具，图（1）、图（2）是我国某环形粒子加速器的实景图和构造原理图，图（3）是粒子加速器的俯视示意图，其中粒子真空室可看作⊙O ，粒子在A点注入，经过优弧 $\text{[math]}$ 后，在B点引出，粒子注入和引出路径都与⊙O相切，C ， D是两个加速电极，粒子在经过 $\text{[math]}$ 时被加速．已知AB＝16km ，粒子注入路径与AB的夹角α＝53°， $\text{[math]}$ 所对的圆心角是90°．
1. （1）求⊙O的直径；
2. （2）比较 $\text{[math]}$ 与AB的长度哪个更长．（相关数据： $\text{[math]}$ ）
答案解析收藏纠错 + 选题

二、新题型-项目式学习

8. (2024·浙江模拟) 根据以下素材，探索完成任务：

测算雷锋塔的高度
素材1	如图1，雷峰塔前有一斜坡 $\text{[math]}$ ，长为10米，坡度为 $\text{[math]}$ ，高为 $\text{[math]}$
素材2	利用测角仪在斜坡底的点 $\text{[math]}$ 处测得塔尖点 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，在斜坡顶的点 $\text{[math]}$ 处测得塔尖点 $\text{[math]}$ 的仰角为 $\text{[math]}$ （其中点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上，如图2）
素材3	查阅锐角三角函数表	$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
任务1	获取数据	计算斜坡的高度 $\text{[math]}$
任务2	分析计算	通过观察，计算雷峰塔的高度（结果保留整数）

答案解析收藏纠错 + 选题

9. (2024九下·汕头月考) 在综合实践课上，数学兴趣小组用所学的数学知识来解决实际问题.实践报告如下：

活动课题	测量两幢楼楼顶之间的距离
活动工具	测角仪、皮尺等
测量过程	【步骤一】如图，在楼AB和楼CD之间竖直放置测角仪MN，其中测角仪的底端M与楼的底部A，C在同一条水平直线上，图中所有点均在同一平面内；【步骤二】利用测角仪测出楼顶B的仰角∠BNE=45°，楼顶D的仰角∠DNF=68.2° 【步骤三】利用皮尺测出AM=40米，CM=20米.
解决问题	根据以上数据计算两幢楼楼顶B，D之间的距离

请你帮助兴趣小组解决以上问题.（计算结果保留整数）

参考数据：sin68.2°≈0.93，cos68.2°≈0.37，tan68.2°≈2.50， $\text{[math]}$ ≈6.08

答案解析收藏纠错 + 选题

10. (2024九下·吉林月考) 城市雕塑“摇橹人”位于吉林市吉林大街南端的江城广场，雕塑人物以几乎倾斜倒地的姿势，用尽全身力气来摆动船橹，代表着吉林人民在湍流江水之中奋力拼搏的精神.某校数学活动小组要测量“摇橹人”的高度，张明同学带领小组成员进行此项实践活动，活动步棸记录如下：
【步骤一】设计测量方案：小组成员讨论后，画出如图①的测量草图，确定需测的几何量.
【步骤二】准备测量工具：皮尺和自制测高仪.其中测高仪 $\text{[math]}$ （如图②）为正方形木板，在顶点 $\text{[math]}$ 处用细线挂一个铅锤 $\text{[math]}$ .
【步骤三】实地测量并记录数据：如图③，令测高仪上的顶点 $\text{[math]}$ ， $\text{[math]}$ 与“摇橹人”最高点 $\text{[math]}$ 在同一条直线上.通过测量得到， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
【步骤四】计算“摇橹人”高度 $\text{[math]}$ .（结果精确到0.1m）（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
现在，请你结合图③和相关数据完成【步骤四】.

答案解析收藏纠错 + 选题

11. (2024九下·定海开学考) 仁皇阁是一个著名景点，某校九年级研学期间参观了仁皇阁，数学兴趣小组对仁皇阁高度产生了浓厚的兴趣，他们想运用所学知识估算出仁皇阁的高度。

课题	估算仁皇阁高度
测量工具	测量角度的仪器，皮尺，刻度尺等
组别	测量方案示意图	测量方案说明
组1		如图1 ，先在仁皇阁底部广场的C处用仪器测得阁楼顶端A的仰角为27° ，然后从C处向阁楼底部前进10m到达D处，此时在D处测得阁楼顶端A的仰角为30° ．
组2		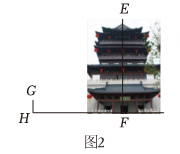如图2 ，身高1.5m的组员站在仁皇阁正门边上合影．打印出照片后量得此组员图上高度GH为0.5cm，量得仁皇阁图上高度EF为12.9cm.

（1）任务一请分别计算两组中测量得到的阁楼高度；（结果保留小数点后一位．参考数据 $\text{[math]}$ ）
（2）任务二后续经过查证后发现小组2数据更为精确，请你帮小组1分析可能产生误差的原因．（写出一条即可）

答案解析收藏纠错 + 选题

12. (2023八上·孟村期中) 廊坊某初中数学兴趣小组为测量路灯高度，设计了如下方案，请据此求出路灯高度 $\text{[math]}$ .

主题	测量路灯高度 $\text{[math]}$
工具	测角仪、皮尺等
人员	组长：xxx；组员：xxx、xxx、xxx
示意图
方案	在路灯前选一点P，并测出 $\text{[math]}$ ，然后把说明竖直竹竿 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上左右移动到某处， $\text{[math]}$ 地面， $\text{[math]}$ 地面处，并测出 $\text{[math]}$ .
数据	$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
评价

答案解析收藏纠错 + 选题

13. (2024·浙江模拟)

教学实践活动： $\text{[math]}$ 班测量雷峰塔高度实践的相关数据
活动 $\text{[math]}$	如图， $\text{[math]}$ 点为塔顶，将 $\text{[math]}$ 根木棒立在 $\text{[math]}$ 处， $\text{[math]}$ 的连线交地面于 $\text{[math]}$ 点，同理将相同长度的木棒立在 $\text{[math]}$ 处，同时得到 $\text{[math]}$ 点 $\text{[math]}$ 若移动木棒使得 $\text{[math]}$ ，在 $\text{[math]}$ 点的仰角为 $\text{[math]}$ ，则 $\text{[math]}$ ▲ ．
活动 $\text{[math]}$	如图，小组 $\text{[math]}$ 设计了此测量方法，若 $\text{[math]}$ 的长度为 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，则可以得到塔的高度大约为 ▲ $\text{[math]}$ 参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
总结与取优
老师做了一个小小的总结，并且设计了一个新的方案，已知塔前有一高 $\text{[math]}$ 米的小树 $\text{[math]}$ ，发现水平地面上点 $\text{[math]}$ 、树顶和塔顶 $\text{[math]}$ 恰好在一条直线上，测得 $\text{[math]}$ 米， $\text{[math]}$ 、 $\text{[math]}$ 之间有一个花圃无法测量，然后在 $\text{[math]}$ 处放置一个平面镜，沿 $\text{[math]}$ 后退，退到 $\text{[math]}$ 处恰好在平面中看到树顶 $\text{[math]}$ 的像，此时 $\text{[math]}$ 米，测量者眼睛到地面的距离 $\text{[math]}$ 为 $\text{[math]}$ 米，求出塔高 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、新考法-解题策略开放

14. (2023九上·房山期中) 同学们在探究学习中发现：“三角形内角的角平分线分对边所得的两条线段与这个角的两边对应成比例” $\text{[math]}$ 下面是小明同学思考出的两种不同的证明方法，请选择其中一种完成证明．
已知：如图， $\text{[math]}$ 中， $\text{[math]}$ 是角平分线．求证： $\text{[math]}$ ．
方法一证明：如图，过点 $\text{[math]}$ 作 $\text{[math]}$ ，与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ．
方法二证明：如图，过点 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

15. (2024·吴兴期末) 如图，在△ABC中，AB＝AC，D、E、F分别是BC、AB、AC的中点，连结DE、DF，求证：DE＝DF．

针对这道题，三位同学进行了如下讨论﹣﹣

小胡：“需要利用全等证明．”

小吴：“要证中线相等，我想到了直角三角形．”

小明：“我觉得你们都对，但还有别的方法．”

请你结合上述讨论，选择恰当的方法完成证明．

答案解析收藏纠错 + 选题

16. (2022九上·顺义期末) 在证明圆周角定理时，某学习小组讨论出圆心与圆周角有三种不同的位置关系（如图1，2，3所示），小敏说：当圆心O在∠ACB的边上时，只要利用三角形内角和定理的推论和等腰三角形的性质即可证明．小亮说：当圆心O在∠ACB的内部或外部时，可以通过添加直径这条辅助线，把问题转化为圆心O在∠ACB的边上时的特殊情形来解决．请选择图2或图3中的一种，完成证明．
圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半．已知：如图，在 $\text{[math]}$ 中， $\text{[math]}$ 所对的圆周角是∠ACB，圆心角是∠AOB．
求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2019·防城模拟) 如图，在△ABC中，AB＝AC，D是底边BC的中点，作DE⊥AB于E，DF⊥AC于F
求证：DE＝DF.

证明：∵AB＝AC，∴∠B＝∠C①.

在△BDE和△CDF中，∠B＝∠C，∠BED＝∠CFD，BD＝CD，∴△BDE≌△CDF②.∴DE＝DF③.
1. （1）上面的证明过程是否正确？若正确，请写出①、②和③的推理根据.
2. （2）请你写出另一种证明此题的方法.
答案解析收藏纠错 + 选题
18. (2021八上·遵义期末) 小明遇到这样一个问题

如图1，△ABC中，∠ACB=90°，点D在AB上，且BD=BC，求证：∠ABC=2∠ACD.

小明发现，除了直接用角度计算的方法外，还可以用下面两种方法：

方法2：如图2，作BE⊥CD，垂足为点E.

方法3：如图3，作CF⊥AB，垂足为点F.

根据阅读材料，从三种方法中任选一种方法，证明∠ABC=2∠ACD.

答案解析收藏纠错 + 选题
19. (2020七下·鼓楼期末) 用两种方法证明“三角形的外角和等于360°”；如图，

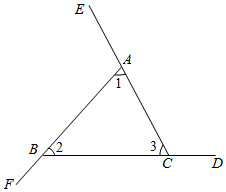
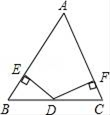
∠BAE、∠CBF、∠ACD是△ABC的三个外角.求证：∠BAE+∠CBF+∠ACD=360°

证法1：∵∠BAE、∠CBF、∠ACD是△ABC的三个外角

∴__▲_.

∴∠BAE+∠CBF+∠ACD=2（∠1+∠2+∠3）

∵_▲_.

∴∠BAE+∠CBF+∠ACD=360°

请把证法1补充完整，并用不同的方法完成证法2

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

备考2024年中考数学重难创新题4 与三角形有关的证明与计...

副标题：

*注意事项：

备考2024年中考数学重难创新题4 与三角形有关的证明与计...

试题分析

总体分析

题量分析

难度分析

知识点分析

已知：如图， $\text{[math]}$ 中， $\text{[math]}$ 是角平分线．求证： $\text{[math]}$ ．
方法一证明：如图，过点 $\text{[math]}$ 作 $\text{[math]}$ ，与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ．	方法二证明：如图，过点 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ．