2024年中考数学考前20天终极冲刺专题之四边形(二)

更新时间：2024-05-21 浏览次数：57 类型：三轮冲刺

一、选择题

1. (2019八下·腾冲期中) 如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD，AC于点E，O，连接CE，则CE的长为（）

A . 3 B . 3.5 C . 2.5 D . 2.8

答案解析收藏纠错 + 选题
2. (2024八下·潮安期中) 在矩形ABCD中，对角线AC、BD相交于点O ， AE平分∠BAD交BC于点E ， ∠CAE＝15°，连接OE ，则下面的结论中正确的有（　　）
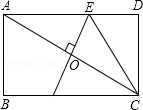
①△DOC是等边三角形；②△BOE是等腰三角形；③BC＝ $\text{[math]}$ AB；④∠AOE＝135°；⑤S_△_AOE＝S_△_BOE ．

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
3. (2017·天门) 如图，矩形ABCD中，AE⊥BD于点E，CF平分∠BCD，交EA的延长线于点F，且BC=4，CD=2，给出下列结论：①∠BAE=∠CAD；②∠DBC=30°；③AE= $\text{[math]}$ ；④AF=2 $\text{[math]}$ ，其中正确结论的个数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
4. (2024九下·深圳开学考) 如图，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④当 $\text{[math]}$ 是 $\text{[math]}$ 的中点时， $\text{[math]}$ ；⑤当 $\text{[math]}$ 时， $\text{[math]}$ ．其中正确结论的序号是 $\text{[math]}$ 　　 $\text{[math]}$

A . ①②③④ B . ①②③⑤ C . ①③④⑤ D . ②④⑤

答案解析收藏纠错 + 选题
5. (2024九下·福田开学考) 如图，在正方形ABCD中，M是边CD上一点，满足 $\text{[math]}$ ，连接BM交AC于点N，延长BN到点P使得 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·沂南模拟) 如图，已知 $\text{[math]}$ 是等边三角形，点D、E分别在边AB、BC上，CD、AE交于点F， $\text{[math]}$ ． FG为 $\text{[math]}$ 的角平分线，点H在FG的延长线上， $\text{[math]}$ ，连接HA、HC．① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；其中说法正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7. 如图，在 Rt△ABC中，LACB=90°，以其三边为边在AB的同侧作三个正方形，点F在GH 上，CG与EF相交于点P，CM 与BE相交于点Q.若HF=FG则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022九下·重庆开学考) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 分别是边 $\text{[math]}$ 、 $\text{[math]}$ 上的点， $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与对角线 $\text{[math]}$ 交于点 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . 6

答案解析收藏纠错 + 选题
9. (2022九下·长沙开学考) 如图，已知在矩形ABCD中，M是AD边的中点，BM与AC垂直，交直线AC于点N，连接DN，则下列四个结论中：①CN＝2AN；②DN＝DC；③tan∠CAD＝ $\text{[math]}$ ；④△AMN∽△CAB.正确的有（）

A . ①②③④ B . ①②③ C . ①②④ D . ②③④

答案解析收藏纠错 + 选题
10. (2023九上·南山期中) 如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，点G是EF的中点，连接CG、BG、BD、DG，下列结论：①BC＝DF；②∠ABG+∠ADG＝180°；③AC：BG＝ $\text{[math]}$ ：1；④若 $\text{[math]}$ ，则4S_△_BDG＝25S_△_DGF ．正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·大庆月考) 如图，正方形ABCD中，AD=4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若点F是AB的中点，则△EMN的周长是．

答案解析收藏纠错 + 选题
12. (2024·叙州模拟) 如图，在正方形 $\text{[math]}$ 中，点E是 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ 与对角线 $\text{[math]}$ 交于点P ，过点P作 $\text{[math]}$ 交 $\text{[math]}$ 于点F ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点G ，
下列四个结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ．其中正确结论有．

答案解析收藏纠错 + 选题
13. (2024·雅安模拟) 如图，正方形 $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ ，垂足为 $\text{[math]}$ ，且交 $\text{[math]}$ 于点 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，延长 $\text{[math]}$ 至 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，有如下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ．
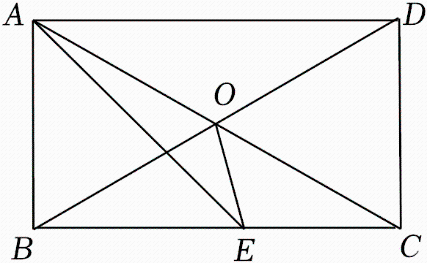
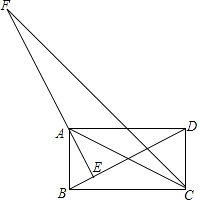
上述结论中，所有正确结论的序号是．

答案解析收藏纠错 + 选题
14. (2022·坪山模拟) 如图，在正方形ABCD中， $\text{[math]}$ ， M为对角线BD上任意一点（不与B、D重合），连接CM，过点M作MN⊥CM，交线段AB于点N．连接NC交BD于点G．若BG：MG＝3：5，则NG⋅CG的值为．

答案解析收藏纠错 + 选题
15. (2024八下·东莞月考) 如图，正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别在线段 $\text{[math]}$ 上运动，且满足 $\text{[math]}$ ， $\text{[math]}$ 分别与 BD 相交于点 $\text{[math]}$ ，下列说法中：① $\text{[math]}$ ；②点 A到线段 EF的距离一定等于正方形的边长；③若 $\text{[math]}$ ，则 $\text{[math]}$ ；④若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．其中结论正确的是；（将正确的序号填写在横线上）

答案解析收藏纠错 + 选题

三、解答题

16. (2017八下·广州期中) 如图，已知四边形ABCD为正方形，AB= $\text{[math]}$ ，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE．交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
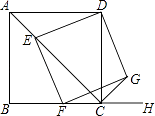
①求证：矩形DEFG是正方形；
②探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．

答案解析收藏纠错 + 选题
17. (2024·成都模拟)
1. （1）如图1，在直角 $\text{[math]}$ 中， $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）如图2，在菱形 $\text{[math]}$ 中，过 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 边于点 $\text{[math]}$ ． ①若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；②若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值（用含 $\text{[math]}$ 的式子表示）；
3. （3）如图3，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 且 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求 $\text{[math]}$ 的值（用含 $\text{[math]}$ 的式子表示）．
答案解析收藏纠错 + 选题

四、实践探究题

18. (2024九下·长春月考) 如图1，点E为正方形ABCD内一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将直角三角形ABE绕点A逆时针方向旋转 $\text{[math]}$ 度（ $\text{[math]}$ ）点B、E的对应点分别为点 $\text{[math]}$ 、 $\text{[math]}$ ．
1. （1）【感知】如图2，在旋转的过程中，点 $\text{[math]}$ 落在了AC上，求此时 $\text{[math]}$ 的长；
2. （2）【探究】若 $\text{[math]}$ ，如图3，得到 $\text{[math]}$ （此时 $\text{[math]}$ 与D重合），延长BE交 $\text{[math]}$ 于点F ，试判断四边形 $\text{[math]}$ 的形状，并说明理由；
3. （3）【应用】在直角三角形ABE绕点A逆时针方向旋转过程中，直接写出线段 $\text{[math]}$ 长度的取值范围．
答案解析收藏纠错 + 选题
19. (2024·佛山模拟) 综合与实践
数学活动课上，同学们用尺规作图法探究在菱形内部作一点到该菱形三个顶点的距离相等．

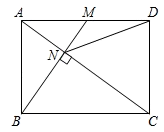
【动手操作】如题图1，已知菱形ABCD，求作点 $\text{[math]}$ ，使得点 $\text{[math]}$ 到三个顶点A，D，C的距离相等.小红同学设计如下步骤：
①连接BD
②分别以点A，D为圆心，大于 $\text{[math]}$ 的长为半径分别在AD的上方与下方作弧；AD上方两弧交于点 $\text{[math]}$ ，下方两弧交于点 $\text{[math]}$ ，作直线MN交BD于点 $\text{[math]}$ ．
③连接AE，EC，则 $\text{[math]}$ ．
1. （1）根据小红同学设计的尺规作图步骤，在题图1中完成作图过程（要求：用尺规作图并保留作图痕迹）．
2. （2）【证明结论】证明： $\text{[math]}$ ．
3. （3）【拓展延伸】当 $\text{[math]}$ 时，求 $\text{[math]}$ 与 $\text{[math]}$ 的面积比．
答案解析收藏纠错 + 选题

五、综合题

20. (2024八下·杭州期中) 如图1，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 为钝角， $\text{[math]}$ ， $\text{[math]}$ 分别为边 $\text{[math]}$ ， $\text{[math]}$ 上的高，交边 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ ；
3. （3）如图2，若 $\text{[math]}$ ，以点 $\text{[math]}$ 为原点建立平面直角坐标系，点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 为直线 $\text{[math]}$ 上一动点，当 $\text{[math]}$ 时，求出此时点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
21. (2023九下·长沙月考) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ 、 $\text{[math]}$ 上，且 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）如图1，当 $\text{[math]}$ 时，求证： $\text{[math]}$ ；
2. （2）如图2， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）如图3，在第（2）的条件下，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
22. (2024八下·北仑期中) 已知在平行四边形ABCD中，动点P在AD边上，以每秒0.5cm的速度从点A向点D运动．
1. （1）如图1，在运动过程中，若CP平分∠BCD ，且满足CD＝CP ，则∠B=°．
2. （2）如图2，另一动点Q在BC边上，以每秒2cm的速度从点C出发，在BC间往返运动，P ， Q两点同时出发，当点P到达点D时停止运动（同时Q点也停止），若AD＝6cm ，当运动时间为秒时，以P ， D ， Q ， B四点组成的四边形是平行四边形．
3. （3）如图3，连结BP并延长与CD的延长线交于点F ， CE平分∠ACF交BF于E点，连接AE ，当AE⊥CE ， DF＝8时，求AC的长．
4. （4）如图4，在（1）的条件下，连结BP并延长与CD的延长线交于点F ，连结AF ，若AB＝4cm ，求△APF的面积．
答案解析收藏纠错 + 选题