

①请你判断四边形的形状,并证明;
②求的长;
①当=2时,求BP的长;
②直接写出BP的取值范围.
[动手操作]如图①,将矩形纸片ABCD对折,使AD与BC重合,展平纸片,得到折痕EF;折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AM,点B,E的对应点分别为B',E',展平纸片,连结AB',BB',BE'.请完成:

①求证: .
②若 ,
, 求折痕
的长.
③当为等腰三角形时,直接写出a,b之间应满足的数量关系.

①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE S菱形ABCD
下列判断正确的是( )

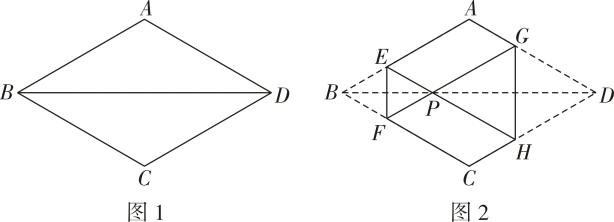

①用t的代数式表示O'和R'的坐标;
②要使该菱形始终与反比例函数图象有交点,求t的取值范围。
①用t的代数式表示O'和R'的坐标;
②要使该菱形始终与反比例函数图象有交点,求t的取值范围。

甲:如图①进行两次折叠,每次折叠后折痕两侧部分能完全重合,故判断原四边形是正方形;
乙:如图②进行两次折叠,每次折叠后折痕两侧部分能完全重合,故判断原四边形是正方形.
下列判断正确的是( )




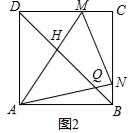
探究①当在
上运动时,
的周长是否会变化?如变化,请说明理由;如不变,请求出该定值.
探究②直接写出四边形面积的最小值.