全国历年中考数学真题精选汇编：三角形2

更新时间：2021-07-08 浏览次数：123 类型：二轮复习

一、单选题

1. (2023八上·余姚期中) △BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）

A . △ABC的周长 B . △AFH的周长 C . 四边形FBGH的周长 D . 四边形ADEC的周长

答案解析收藏纠错 + 选题
2. (2022·眉山模拟) 如图是用8块A型瓷砖（白色四边形）和8块B型瓷砖（黑色三角形）不重叠、无空隙拼接而成的一个正方形图案，图案中A型瓷砖的总面积与B型瓷砖的总面积之比为（）

A . $\text{[math]}$ ：1 B . 3：2 C . $\text{[math]}$ ：1 D . $\text{[math]}$ ：2

答案解析收藏纠错 + 选题
3. 如图，在 $\text{[math]}$ 的正方形网格中有两个格点A、B，连接 $\text{[math]}$ ，在网格中再找一个格点C，使得 $\text{[math]}$ 是等腰直角三角形，满足条件的格点C的个数是（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
4. (2024·寻乌模拟) 如图，在菱形ABCD中，AB=2，∠A=120°，过菱形ABCD的对称中心O分别作边AB，BC的垂线，交各边于点E，F，G，H.则四边形EFGH的周长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022七下·双城期末) 如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
6.
如图，AD是△ABC的角平分线，则AB：AC等于（　　）

A . BD：CD B . AD：CD C . BC：AD D . BC：AC

答案解析收藏纠错 + 选题
7. (2021八上·肥西期末) 如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
8. (2017·鄂州) 如图四边形ABCD中，AD∥BC，∠BCD=90°，AB=BC+AD，∠DAC=45°，E为CD上一点，且∠BAE=45°．若CD=4，则△ABE的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2018·台州) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ .若图中阴影部分的面积与正方形 $\text{[math]}$ 的面积之比为 $\text{[math]}$ ，则 $\text{[math]}$ 的周长为．

答案解析收藏纠错 + 选题
10. (2017·徐州) 如图，已知OB=1，以OB为直角边作等腰直角三角形A₁BO，再以OA₁为直角边作等腰直角三角形A₂A₁O，如此下去，则线段OA_n的长度为．

答案解析收藏纠错 + 选题
11. (2021八下·南岗期末) 把两个同样大小含 $\text{[math]}$ 角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 $\text{[math]}$ ，且另外三个锐角顶点 $\text{[math]}$ 在同一直线上．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2019·鄂州) 如图，已知线段AB＝4，O是AB的中点，直线l经过点O，∠1＝60°，P点是直线l上一点，当△APB为直角三角形时，则BP＝.

答案解析收藏纠错 + 选题
13. (2017·娄底) 如图，在等腰Rt△ABC中，∠ABC=90°，AB=CB=2，点D为AC的中点，点E，F分别是线段AB，CB上的动点，且∠EDF=90°，若ED的长为m，则△BEF的周长是（用含m的代数式表示）

答案解析收藏纠错 + 选题
14. (2022·四会模拟) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，取大于 $\text{[math]}$ 的长为半径，分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心作弧相交于两点，过此两点的直线交 $\text{[math]}$ 边于点 $\text{[math]}$ （作图痕迹如图所示），连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
15. (2022·肇源模拟) 有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上， $\text{[math]}$ 长度始终保持不变， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，点 $\text{[math]}$ 到 $\text{[math]}$ ， $\text{[math]}$ 的距离分别为4和2．在此滑动过程中，猫与老鼠的距离 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
16. (2023八下·自贡月考) 如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∠DAM=45°，点F在射线AM上，且 $\text{[math]}$ ，CF与AD相交于点G，连接EC，EF，EG，则下列结论：①∠ECF=45°；② $\text{[math]}$ 的周长为 $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ 的面积的最大值 $\text{[math]}$ .其中正确的结论是.（填写所有正确结论的序号）

答案解析收藏纠错 + 选题
17. (2014·柳州)
如图，在△ABC中，分别以AC，BC为边作等边△ACD和等边△BCE．设△ACD、△BCE、△ABC的面积分别是S₁、S₂、S₃ ，现有如下结论：

①S₁：S₂=AC²：BC²；
②连接AE，BD，则△BCD≌△ECA；
③若AC⊥BC，则S₁•S₂= $\text{[math]}$ S₃² ．
其中结论正确的序号是．

答案解析收藏纠错 + 选题
18. (2016·河北) 如图，已知∠AOB=7°，一条光线从点A出发后射向OB边.若光线与OB边垂直，则光线沿原路返回到点A，此时∠A=90°-7°=83°.

当∠A<83°时，光线射到OB边上的点A₁后，经OB反射到线段AO上的点A₂ ，易知∠1=∠2.若A₁A₂⊥AO ，光线又会沿A₂→A₁→A原路返回到点A，此时∠A=°.

若光线从点A发出后，经若干次反射能沿原路返回到点A ，则锐角∠A的最小值=°.

答案解析收藏纠错 + 选题

三、解答题

19. (2017·绍兴)
已知△ABC，AB=AC，D为直线BC上一点，E为直线AC上一点，AD=AE，设∠BAD=α，∠CDE=β.
1. （1）如图，若点D在线段BC上，点E在线段AC上.
  ①如果∠ABC=60°，∠ADE=70°，那么α=°，β=°.②求α，β之间的关系式.
2. （2）是否存在不同于以上②中的α，β之间的关系式？若存在，请求出这个关系式（求出一个即可）；若不存在，说明理由.
答案解析收藏纠错 + 选题
20. (2017·衢州)
问题背景
如图1，在正方形ABCD的内部，作∠DAE=∠ABF=∠BCG=∠CDH，根据三角形全等的条件，易得△DAE≌△ABF≌△BCG≌△CDH，从而得到四边形EFGH是正方形。
类比研究
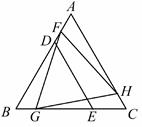
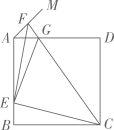
如图2，在正△ABC的内部，作∠BAD=∠CBE=∠ACF，AD，BE，CF两两相交于D，E，F三点（D，E，F三点不重合）。
1. （1） △ABD，△BCE，△CAF是否全等？如果是，请选择其中一对进行证明；
2. （2） △DEF是否为正三角形？请说明理由；
3. （3）进一步探究发现，△ABD的三边存在一定的等量关系，设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请探索 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足的等量关系。
答案解析收藏纠错 + 选题
21. (2019·临沂) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上一点，(与 $\text{[math]}$ 、 $\text{[math]}$ 不重合)，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 所在的直线折叠得到 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，连接 $\text{[math]}$ ，作 $\text{[math]}$ ，与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．显然 $\text{[math]}$ 是 $\text{[math]}$ 的平分线， $\text{[math]}$ 是 $\text{[math]}$ 的平分线．仔细观察，请逐一找出图中其他的角平分线(仅限于小于 $\text{[math]}$ 的角平分线)，并说明理由．

答案解析收藏纠错 + 选题

四、综合题

22. (2019·台州) 我们知道，各个角都相等，各条边都相等的多边形叫做正多边形，对一个各条边都相等的凸多边形（边数大于3），可以由若干条对角线相等判定它是正多边形.例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形
1. （1）已知凸五边形ABCDE的各条边都相等
  ①如图1，若AC=AD=BE=BD=CE，求证：五边形ABCDE是正五边形
  
  ②2如图2，若AC=BE=CE，请判断五边形ABCDE是不是正五边形，并说明理由
2. （2）判断下列命题的真假，（在括号内填写“真”或“假”），如图3，已知凸六边形ABCDEF的各条边都相等
  ①若AC=CE=EA，则六边形ABCDEF是正六边形（）
  
  ②若AD=BE=CF，则六边形ABCDEF是正六边形（）
答案解析收藏纠错 + 选题
23. (2013·温州)
如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6，0），B（0，8），点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴上的一动点，连接CD，DE，以CD，DE为边作▱CDEF．
1. （1）当0＜m＜8时，求CE的长（用含m的代数式表示）；
2. （2）当m=3时，是否存在点D，使▱CDEF的顶点F恰好落在y轴上？若存在，求出点D的坐标；若不存在，请说明理由；
3. （3）点D在整个运动过程中，若存在唯一的位置，使得▱CDEF为矩形，请求出所有满足条件的m的值．
答案解析收藏纠错 + 选题
24. (2013·台州)
如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．
1. （1）请用直尺和圆规画一个“好玩三角形”；
2. （2）如图在Rt△ABC中，∠C=90°，tanA= $\text{[math]}$ ，求证：△ABC是“好玩三角形”；
3. （3）如图2，已知菱形ABCD的边长为a，∠ABC=2β，点P，Q从点A同时出发，以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动，记点P经过的路程为s．
  ①当β=45°时，若△APQ是“好玩三角形”，试求 $\text{[math]}$ 的值；
  ②当tanβ的取值在什么范围内，点P，Q在运动过程中，有且只有一个△APQ能成为“好玩三角形”．请直接写出tanβ的取值范围．
4. （4）（本小题为选做题）
  依据（3）的条件，提出一个关于“在点P，Q的运动过程中，tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题（“好玩三角形”的个数限定不能为1）
答案解析收藏纠错 + 选题
25. (2013·宁波)
若一个四边形的一条对角线把四边形分成两个等腰三角形，我们把这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如菱形就是和谐四边形．
1. （1）如图1，在梯形ABCD中，AD∥BC，∠BAD=120°，∠C=75°，BD平分∠ABC．求证：BD是梯形ABCD的和谐线；
2. （2）如图2，在12×16的网格图上（每个小正方形的边长为1）有一个扇形BAC，点A．B．C均在格点上，请在答题卷给出的两个网格图上各找一个点D，使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线，并画出相应的和谐四边形；
3. （3）四边形ABCD中，AB=AD=BC，∠BAD=90°，AC是四边形ABCD的和谐线，求∠BCD的度数．
答案解析收藏纠错 + 选题
26. (2013·湖州)
一节数学课后，老师布置了一道课后练习题：
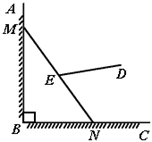
如图，已知在Rt△ABC中，AB=BC，∠ABC=90°，BO⊥AC于点O，点P、D分别在AO和BC上，PB=PD，DE⊥AC于点E，求证：△BPO≌△PDE．
1. （1）
  理清思路完成解答
  本题证明的思路可用下列框图表示：
  根据上述思路，请你完整地书写本题的证明过程．
2. （2）若PB平分∠ABO，其余条件不变．求证：AP=CD．
3. （3）知识迁移，探索新知
  若点P是一个动点，点P运动到OC的中点P′时，满足题中条件的点D也随之在直线BC上运动到点D′，请直接写出CD′与AP′的数量关系．（不必写解答过程）
答案解析收藏纠错 + 选题
27. (2014·南京) 【问题提出】
学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
1. （1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据，可以知道Rt△ABC≌Rt△DEF．
  第二种情况：当∠B是钝角时，△ABC≌△DEF．
2. （2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．
  第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
3. （3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
4. （4） ∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若，则△ABC≌△DEF．
答案解析收藏纠错 + 选题
28. (2022七上·牟平期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）如图1，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，当 $\text{[math]}$ ， $\text{[math]}$ 时，求线段 $\text{[math]}$ 的长；
2. （2）如图2，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）如图3，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
29. (2018·日照) 问题背景：我们学习等边三角形时得到直角三角形的一个性质：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．即：如图1，在Rt△ABC中，∠ACB=90°，∠ABC=30°，则：AC= $\text{[math]}$ AB．
探究结论：小明同学对以上结论作了进一步研究．
1. （1）如图1，连接AB边上中线CE，由于CE= $\text{[math]}$ AB，易得结论：①△ACE为等边三角形；②BE与CE之间的数量关系为．
2. （2）如图2，点D是边CB上任意一点，连接AD，作等边△ADE，且点E在∠ACB的内部，连接BE．试探究线段BE与DE之间的数量关系，写出你的猜想并加以证明．
3. （3）当点D为边CB延长线上任意一点时，在（2）条件的基础上，线段BE与DE之间存在怎样的数量关系？请直接写出你的结论.
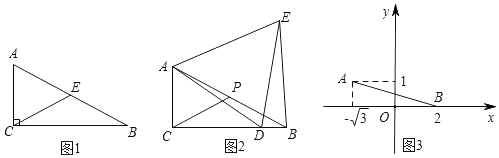
  拓展应用：如图3，在平面直角坐标系xOy中，点A的坐标为（﹣ $\text{[math]}$ ，1），点B是x轴正半轴上的一动点，以AB为边作等边△ABC，当C点在第一象限内，且B（2，0）时，求C点的坐标．
答案解析收藏纠错 + 选题
30. (2017·烟台)
1. （1）
  如图1，△ABC为等边三角形，现将三角板中的60°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于30°），旋转后三角板的一直角边与AB交于点D，在三角板斜边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=30°，连接AF，EF．
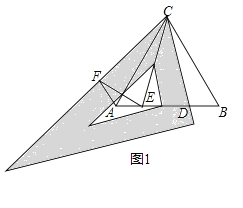
  ①求∠EAF的度数；
  ②DE与EF相等吗？请说明理由；
2. （2）
  如图2，△ABC为等腰直角三角形，∠ACB=90°，先将三角板的90°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于45°），旋转后三角板的一直角边与AB交于点D，在三角板另一直角边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=45°，连接AF，EF，请直接写出探究结果：
  ①求∠EAF的度数；
  ②线段AE，ED，DB之间的数量关系．
答案解析收藏纠错 + 选题
31. (2017·潍坊)
边长为6的等边△ABC中，点D、E分别在AC、BC边上，DE∥AB，EC=2 $\text{[math]}$
1. （1）如图1，将△DEC沿射线方向平移，得到△D′E′C′，边D′E′与AC的交点为M，边C′D′与∠ACC′的角平分线交于点N，当CC′多大时，四边形MCND′为菱形？并说明理由．
2. （2）
  如图2，将△DEC绕点C旋转∠α（0°＜α＜360°），得到△D′E′C，连接AD′、BE′．边D′E′的中点为P．
  ①在旋转过程中，AD′和BE′有怎样的数量关系？并说明理由；
  ②连接AP，当AP最大时，求AD′的值．（结果保留根号）
答案解析收藏纠错 + 选题
32. (2017·临沂)
数学课上，张老师出示了问题：如图1，AC，BD是四边形ABCD的对角线，若∠ACB=∠ACD=∠ABD=∠ADB=60°，则线段BC，CD，AC三者之间有何等量关系？
经过思考，小明展示了一种正确的思路：如图2，延长CB到E，使BE=CD，连接AE，证得△ABE≌△ADC，从而容易证明△ACE是等边三角形，故AC=CE，所以AC=BC+CD．
小亮展示了另一种正确的思路：如图3，将△ABC绕着点A逆时针旋转60°，使AB与AD重合，从而容易证明△ACF是等边三角形，故AC=CF，所以AC=BC+CD．
在此基础上，同学们作了进一步的研究：
1. （1）小颖提出：如图4，如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”，其它条件不变，那么线段BC，CD，AC三者之间有何等量关系？针对小颖提出的问题，请你写出结论，并给出证明．
2. （2）小华提出：如图5，如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”，其它条件不变，那么线段BC，CD，AC三者之间有何等量关系？针对小华提出的问题，请你写出结论，不用证明．
答案解析收藏纠错 + 选题
33. (2016·泰安)
按要求回答问题：
1. （1）已知：△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是直线BC上一点，且∠DEC=∠DCE，若∠A=60°（如图①）．求证：EB=AD；
2. （2）若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其它条件不变（如图②），（1）的结论是否成立，并说明理由；
3. （3）若将（1）中的“若∠A=60°”改为“若∠A=90°”，其它条件不变，则 $\text{[math]}$ 的值是多少？（直接写出结论，不要求写解答过程）
答案解析收藏纠错 + 选题
34. (2017·天门) 在Rt△ABC中，∠ACB=90°，点D与点B在AC同侧，∠DAC＞∠BAC，且DA=DC，过点B作BE∥DA交DC于点E，M为AB的中点，连接MD，ME．
1. （1）
  如图1，当∠ADC=90°时，线段MD与ME的数量关系是；
2. （2）
  如图2，当∠ADC=60°时，试探究线段MD与ME的数量关系，并证明你的结论；
3. （3）
  如图3，当∠ADC=α时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
35. (2018·衡阳) 如图，在Rt $\text{[math]}$ ABC中，∠C=90°，AC=BC=4cm，动点P从点C出发以1cm/s的速度沿CA匀速运动，同时动点Q从点A出发以 $\text{[math]}$ 的速度沿AB匀速运动，当点P到达点A时，点P、Q同时停止运动，设运动时间为他t(s)．
1. （1）当t为何值时，点B在线段PQ的垂直平分线上？
2. （2）是否存在某一时刻t，使 $\text{[math]}$ APQ是以PQ为腰的等腰三角形？若存在，求出 $\text{[math]}$ 的值；若不存在，请说明理由；
3. （3）以PC为边，往CB方向作正方形CPMN，设四边形QNCP的面积为S，求S关于t的函数关系式．
答案解析收藏纠错 + 选题
36. (2014·韶关)
如图，在△ABC中，AB=AC，AD⊥BC于点D，BC=10cm，AD=8cm．点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t＞0）．
1. （1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形；
2. （2）在整个运动过程中，所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长；
3. （3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
37. (2014·北海)
如图（1），E是正方形ABCD的边BC上的一个点（E与B、C两点不重合），过点E作射线EP⊥AE，在射线EP上截取线段EF，使得EF=AE；过点F作FG⊥BC交BC的延长线于点G．
1. （1）求证：FG=BE；
2. （2）连接CF，如图（2），求证：CF平分∠DCG；
3. （3）当 $\text{[math]}$ = $\text{[math]}$ 时，求sin∠CFE的值．
答案解析收藏纠错 + 选题
38. (2021·重庆) 在等边 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，垂足为D，点E为AB边上一点，点F为直线BD上一点，连接EF.
1. （1）将线段EF绕点E逆时针旋转60°得到线段EG，连接FG.
  ①如图1，当点E与点B重合，且GF的延长线过点C时，连接DG，求线段DG的长；
  
  ②如图2，点E不与点A，B重合，GF的延长线交BC边于点H，连接EH，求证： $\text{[math]}$ ；
2. （2）如图3，当点E为AB中点时，点M为BE中点，点N在边AC上，且 $\text{[math]}$ ，点F从BD中点Q沿射线QD运动，将线段EF绕点E顺时针旋转60°得到线段EP，连接FP，当 $\text{[math]}$ 最小时，直接写出 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
39. (2017·重庆) 在△ABC中，∠ABM=45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．
1. （1）如图1，若AB=3 $\text{[math]}$ ，BC=5，求AC的长；
2. （2）如图2，点D是线段AM上一点，MD=MC，点E是△ABC外一点，EC=AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF=∠CEF．
答案解析收藏纠错 + 选题