2022年苏科版初中数学《中考一轮复习》专题四图形的认识 ...

更新时间：2022-01-18 浏览次数：98 类型：一轮复习

一、单选题

1. (2024九上·南山月考) 下列命题是真命题的是（）

A . 对角线互相垂直平分的四边形是正方形 B . 对角线相等的四边形是平行四边形 C . 对角线互相垂直的四边形是菱形 D . 对角线互相平分且相等的四边形是矩形

答案解析收藏纠错 + 选题
2. (2021八上·鹿邑期中) 一个多边形截去一个角后，形成新多边形的内角和为2 520°，则原多边形的边数为（　　）

A . 15 B . 16 C . 13或15 D . 15或16或17

答案解析收藏纠错 + 选题
3. (2021九上·新邵期末) 如图，在平行四边形 $\text{[math]}$ 中，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积之比为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021九上·余姚期中) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点， $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 分别交于点 $\text{[math]}$ 、 $\text{[math]}$ ．则下列说法错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021九上·台儿庄期中) 如图，D、E、F分别是 $\text{[math]}$ 各边中点，则以下说法错误的是（）

A . $\text{[math]}$ 和 $\text{[math]}$ 的面积相等 B . 四边形 $\text{[math]}$ 是平行四边形 C . 若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是菱形 D . 若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 是矩形

答案解析收藏纠错 + 选题
6. (2021八下·綦江期末) 如图，平行四边形 $\text{[math]}$ 的对角线交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．如果 $\text{[math]}$ 的周长为7.5，那么平行四边形 $\text{[math]}$ 的周长是（）

A . 7.5 B . 15 C . 17 D . 19

答案解析收藏纠错 + 选题
7. (2021九上·杭州开学考) 如图，正方形 $\text{[math]}$ 的边长为12， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ ， $\text{[math]}$ 边上的点，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ ， $\text{[math]}$ 边上的点，且 $\text{[math]}$ 交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 6 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021八下·慈溪期中) 如图，已知▱OABC的顶点A，C分别在直线 $\text{[math]}$ 和 $\text{[math]}$ 上，O是坐标原点，则对角线OB长的最小值为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
9. (2021八上·平阳期中) 如图，在▱ABCD中，∠A＝60°，AD＝2．以点A为圆心，AD为半径作 $\text{[math]}$ ，交边AB于点E，G是 $\text{[math]}$ 的中点，作GF∥BC交CD于点F，以点F为旋转中心，将线段FG按逆时针方向旋转90°至线段FG′，若点G′恰好落在边BC上，则AB的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021九上·内江期中) 在▱ABCD中，∠DBC＝45°，DE⊥BC于E，BF⊥CD于F，BF交DE于点H，交AD的延长线于点G，下面结论中：①BD＝ $\text{[math]}$ BE；②∠A＝∠BHE；③CD²+BG²＝AG²；④BH×DG＝ED×GH.正确的结论是（）

A . ①②③ B . ②③④ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题

11. (2021八上·陇县期中) 如果一个多边形的内角和是 $\text{[math]}$ ，那么这个多边形的边数是.

答案解析收藏纠错 + 选题
12. (2021八下·长安期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是.

答案解析收藏纠错 + 选题
13. (2021八上·富裕期末) 如图，∠A+∠B+∠C+∠D+∠E+∠F＝．

答案解析收藏纠错 + 选题
14. (2021八上·江津期中) 如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高.若AB+AC＝8，S_△ABC＝24，∠EDF＝120°，则AD的长为 .

答案解析收藏纠错 + 选题
15. (2021九上·四川月考) 如图，AC是平行四边形ABCD的对角线，且AC⊥AB，在AD上截取AH＝AB，连接BH交AC于点F，过点C作CE平分∠ACB交BH于点G，且GF＝2 $\text{[math]}$ ，CG＝6，则AC＝.

答案解析收藏纠错 + 选题
16. (2021八下·双阳期末) 如图，在平行四边形ABCD中，E、F分别是AD、BC边上的点，AF与BE相交于点G ， DF与EC相交于点H ，若S_△ABG＝16，S_△DHC＝7，则四边形EGFH的面积为．

答案解析收藏纠错 + 选题
17. (2021九上·昆明月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ cm， $\text{[math]}$ cm， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，若点 $\text{[math]}$ 以1cm/s的速度从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 向点 $\text{[math]}$ 运动；点 $\text{[math]}$ 同时以2cm/s的速度从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 向点 $\text{[math]}$ 运动，点 $\text{[math]}$ 运动到 $\text{[math]}$ 点时停止运动，点 $\text{[math]}$ 也同时停止运动，当点 $\text{[math]}$ 运动时，以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的四边形是平行四边形．

答案解析收藏纠错 + 选题
18. (2021八下·北仑期末) 如图，一副三角板如图1放置，AB＝CD，顶点E重合，将△DEC绕其顶点E旋转，如图2，在旋转过程中，当∠AED＝75°，连结AD，BC，AC，下列四个结论中说法正确的有 .①四边形ABCD是平行四边形；②CE垂直平分AB；③若AB²＝6，则BC²＝5+2 $\text{[math]}$ ；④DE⊥AC.

答案解析收藏纠错 + 选题

三、综合题

19. (2021八上·鹿邑期中) 一个多边形除一内角外，其余内角和与外角和之和为1560°.
1. （1）求该多边形的边数；
2. （2）若该多边形为正多边形，求每一个外角的度数.
答案解析收藏纠错 + 选题
20. (2021九上·上城月考) 如图，在平行四边形ABCD中，对角线AC、BD交于点O.M为AD中点，连接CM交BD于点N.
1. （1）求DN：BN的值：
2. （2）若ΔOCN的面积为2，求四边形AONM的面积.
答案解析收藏纠错 + 选题
21. (2021九上·建华期末) 如图，在平行四边形ABCD中，过点A分别作AE⊥BC于点E，AF⊥CD于点F．
1. （1）求证：∠BAE=∠DAF；
2. （2）已知AE=4，AF=6，tan∠BAE= $\text{[math]}$ ，求CF的长．
答案解析收藏纠错 + 选题
22. (2021九上·沈北期中) 如图．在▱ABCD中，点E在边BC上，点F在边AD的延长线上，且DF=BE．EF与CD交于点G．
1. （1）求证：BD∥EF ．
2. （2）若 $\text{[math]}$ ，BE=4，求EC的长．
答案解析收藏纠错 + 选题
23. (2021八上·江津期中) 定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
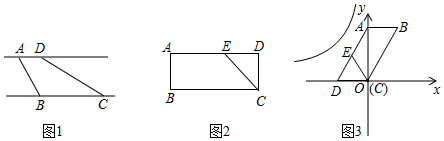
性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等.

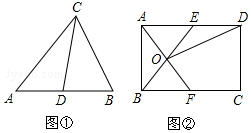
理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S_△ACD=S_△BCD.

应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O.
1. （1）求证：△AOB和△AOE是“友好三角形”；
2. （2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积.
答案解析收藏纠错 + 选题
24. (2021九上·薛城期中) 如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE，F为AE上一点，且∠BFE=∠C
1. （1）求证：△ABF∽△EAD
2. （2）若AB=4，S_ABCD= $\text{[math]}$ ，求AE的长
3. （3）在（1）、（2）条件下，若AD=3，求BF的长（计算结果可含根号）
答案解析收藏纠错 + 选题
25. (2021九上·锦江月考) 综合与实践
问题情境：数学活动课上，老师出示了一个问题：如图①，在平行四边形ABCD中，BE⊥AD，垂足为E，F为CD的中点，连接EF，BF，试猜想EF与BF的数量关系，并加以证明.
1. （1）独立思考：
  请解答老师提出的问题；
2. （2）实践探究：
  希望小组受此问题的启发，将平行四边形ABCD沿着BF（F为CD的中点）所在直线折叠，如图②，点C的对应点为C′，连接DC′并延长交AB于点G，请判断AG与BG的数量关系，并加以证明.
3. （3）问题解决：
  智慧小组突发奇想，将▱ABCD沿过点B的直线折叠，如图③，点A的对应点为A′，使A′B⊥CD于点H，折痕交AD于点M，连接A′M，交CD于点N.该小组提出一个问题：若此平行四边形ABCD的面积为20，边长AB＝5，BC＝2 $\text{[math]}$ ，求图中阴影部分（四边形BHNM）的面积.请你思考此问题，直接写出结果.
答案解析收藏纠错 + 选题
26. (2021八下·苏州期末) 定义：有一组对边平行，有一个内角是它对角的一半的凸四边形叫做半对角四边形，如图1，直线 $\text{[math]}$ ，点A，D在直线 $\text{[math]}$ 上，点B，C在直 $\text{[math]}$ 上，若∠BAD＝2∠BCD，则四边形ABCD是半对角四边形.
1. （1）如图2，点E是矩形ABCD的边AD上一点，AB＝1，AE＝2.若四边形ABCE为半对角四边形，求AD的长：
2. （2）如图3，以▱ABCD的顶点C为坐标原点，边CD所在直线为x轴，对角线AC所在直线为y轴，建立平面直角坐标系.点E是边AD上一点，满足BC＝AE＋CE.求证：四边形ABCE是半对角四边形；
3. （3）在（2）的条件下，当AB＝AE＝ $\text{[math]}$ ，∠B＝60°时，将四边形ABCE向左平移a（a＞0）个单位后，恰有两个顶点落在反比例函数 $\text{[math]}$ 的图象上，求k的值.
答案解析收藏纠错 + 选题