
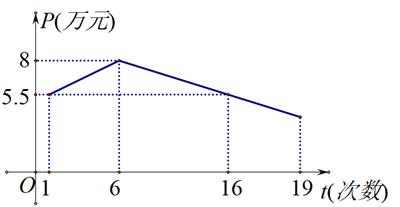
①若x=8,W的值为;
②求W关于x的函数解析式.


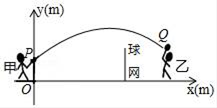
①请直接写出点 的横坐标为(用含字母
的代数式表示)
②当点 落在抛物线上时,请直接写出此时
为秒,点
的坐标为;
③点 是第二象限内一点,当四边形
为矩形时,过抛物线顶点的一条直线将这个矩形分成面积相等的两部分,请直接写出此时
为秒,这条过抛物线顶点的直线表达式为.
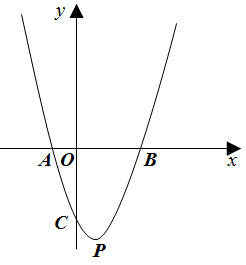
我们通过下列步骤估计方程2x2+x﹣2=0的根的所在的范围.
第一步:画出函数y=2x2+x﹣2的图象,发现图象是一条连续不断的曲线,且与x轴的一个交点的横坐标在0,1之间.
第二步:因为当x=0时,y=﹣2<0;当x=1时,y=1>0.
所以可确定方程2x2+x﹣2=0的一个根x1所在的范围是0<x1<1.
第三步:通过取0和1的平均数缩小x1所在的范围;
取x= ,因为当x=
时,y<0,
又因为当x=1时,y>0,
所以 <x1<1.
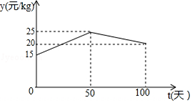
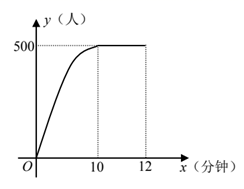
①分别求出当 和
时,
与
的函数关系式;
②设将这批淡水鱼放养 天后一次性出售所得利润为
元,求当
为何值时,
最大?并求出最大值.(利润
销售总额-总成本)
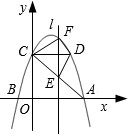
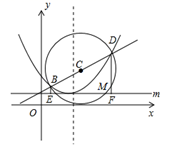
①求四边形 CEDF 面积的最大值.
②若△CDE 是等腰三角形,求点 E 的坐标.
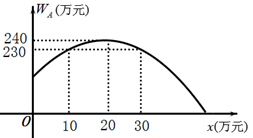
①该店当天线下和网上销售量均为34个,求当天的总纯利润?
②若线下增加的销售量不超过原来线下销售量的 , 该店每天生产多少个蛋糕,可使当天的总纯利润最大?
|
第x年 |
1 |
2 |
3 |
… |
x |
|
售价(元) |
4500 |
4000 |
|
… |
|
|
销售量(百万台) |
14 |
16 |
|
… |
|