备考2023年中考数学嘉兴卷变式阶梯训练：第18题

更新时间：2023-04-15 浏览次数：119 类型：三轮冲刺

一、原题

1. (2024·武汉模拟) 小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB＝OD.求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．

小惠：

证明：∵AC⊥BD，OB＝OD，

∴AC垂直平分BD．

∴AB＝AD，CB＝CD，

∴四边形ABCD是菱形．

小洁：

这个题目还缺少条件，需要补充一个条件才能证明．

若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．

答案解析收藏纠错 + 选题

二、基础

2. (2022·萧山模拟) 如图， $\text{[math]}$ 为锐角，射线 $\text{[math]}$ 射线 $\text{[math]}$ ，作 $\text{[math]}$ 和 $\text{[math]}$ 的平分线分别交 $\text{[math]}$ 和 $\text{[math]}$ 于点 $\text{[math]}$ 和 $\text{[math]}$ ，连接 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 为菱形.

答案解析收藏纠错 + 选题
3. (2021九上·秦都月考) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ .求证：四边形 $\text{[math]}$ 是菱形.

答案解析收藏纠错 + 选题
4. (2022·凤县模拟) 如图，D、E、F分别是 $\text{[math]}$ 各边的中点，连接DE、EF， $\text{[math]}$ ，求证：四边形ADEF为菱形.

答案解析收藏纠错 + 选题
5. (2023九上·武功期末) 如图，在Rt△ABC中，∠ACB=90°，∠ABC=60°，点D为AB的中点，连接CD，过点D作 $\text{[math]}$ ，且DE=BC，连接BE，求证：四边形BCDE是菱形．

答案解析收藏纠错 + 选题
6. (2022九上·榆林月考) 如图，在Rt△ABC中，∠ACB＝90°，D为AB中点，BE∥CD，CE∥AB．试判断四边形BDCE的形状，并证明你的结论．

答案解析收藏纠错 + 选题
7. (2022·榆阳模拟) 如图，矩形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点O，过点B作 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是菱形.

答案解析收藏纠错 + 选题
8. (2022九上·西安月考) 如图，已知△ABC中，D是AC的中点，过点D作DE⊥AC交BC于点E，过点A作AF∥BC交DE于点F，连接AE，CF.求证：四边形AECF是菱形.

答案解析收藏纠错 + 选题
9. (2024·阳新) 如图，四边形 $\text{[math]}$ 是平行四边形，且对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点O， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .

求证：四边形 $\text{[math]}$ 是菱形.

答案解析收藏纠错 + 选题
10. (2022九上·郓城期中) 在 $\text{[math]}$ 中，E、F分别是边BC，AD的中点，AC是对角线，过点D作DP $\text{[math]}$ AC，交BA的延长线于点P，∠P=90°．求证：四边形AECF是菱形．

答案解析收藏纠错 + 选题
11. (2021·蕉岭模拟) 如图，在四边形ABCD中，E，F，G，H分别是AB，BD，CD，AC的中点，AD＝BC，求证：四边形EFGH是菱形．

答案解析收藏纠错 + 选题

三、进阶

12. (2022·浦东模拟) 如图，在四边形ABCD中，AD//BC，E在BC的延长线，连接AE分别交BD、CD于点G、F，且 $\text{[math]}$ ．
1. （1）求证：AB//CD；
2. （2）若 $\text{[math]}$ ， BG=GE，求证：四边形ABCD是菱形．
答案解析收藏纠错 + 选题
13. (2022·丰台模拟) 如图，在四边形ABCD中，∠DCB＝90°，AD $\text{[math]}$ BC，点E在BC上，AB $\text{[math]}$ DE，AE平分∠BAD．
1. （1）求证：四边形ABED为菱形；
2. （2）连接BD，交AE于点O．若AE＝6，sin∠DBE＝ $\text{[math]}$ ，求CD的长．
答案解析收藏纠错 + 选题
14. (2022·昆明模拟) 如图，在平行四边形ABCD中，∠ABC的平分线BE交AD于点E，点F是BC边上的一点，且BF＝AB，连接EF．
1. （1）求证：四边形ABFE是菱形；
2. （2）连接AF，交BE于点O，若AB＝5，BE+AF＝14，求菱形ABFE的面积．
答案解析收藏纠错 + 选题
15. (2022·玉溪模拟) 如图，在平行四边形ABCD中，以A为圆心，AB长为半径画弧交AD于点F；再分别以B、F为圆心，大于 $\text{[math]}$ 的相同长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF，则四边形ABEF是菱形．
1. （1）求证：四边形ABEF是菱形；
2. （2）若菱形ABEF的周长为8， $\text{[math]}$ ，求∠C的大小．
答案解析收藏纠错 + 选题
16. (2022·德宏模拟) 如图所示，在△ABC中，∠ACB＝90°，O、D分别是边AC、AB的中点，过点C作CE//AB交DO的延长线于点E，连接AE．
1. （1）求证：四边形AECD是菱形；
2. （2）若四边形AECD的面积为 $\text{[math]}$ ， $\text{[math]}$ ，求BC的长．
答案解析收藏纠错 + 选题
17. (2022·任城模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点D，点E在线段 $\text{[math]}$ 上，点F在 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
18. (2022·寿光模拟) 如图，在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， E为AD边的一动点（不与端点重合），连接CE并延长，交BA的延长线于点F，延长EA至点G，使 $\text{[math]}$ ，分别连接BE，BG，FG．
1. （1）在点E的运动过程中，四边形BEFG能否成为菱形？请判断并说明理由．
2. （2）若 $\text{[math]}$ 与 $\text{[math]}$ 相似，求AE的长．
答案解析收藏纠错 + 选题
19. (2022·平桂模拟) 如图，在 $\text{[math]}$ 中，AD是BC边上的中线，E是AD的中点，过点A作 $\text{[math]}$ 交BE的延长线于点F，连接CF.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求四边形ADCF的周长.
答案解析收藏纠错 + 选题
20. (2022·东城模拟) 如图，在四边形ABCD中，AC与BD相交于点O，且 $\text{[math]}$ ，点E在BD上， $\text{[math]}$ ．
1. （1）求证：四边形AECD是平行四边形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求BE的长．
答案解析收藏纠错 + 选题

四、突破

21. (2022·临安模拟) ▱ ABCD 中， ∠BAD的平分线交直线 BC 于点 E，线 DC于点 F
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
22. (2022·萍乡模拟) 已知：在Rt△ABC中，∠B=90°，∠ACB=30°，点D为BC边上一动点，以AD为边，在AD的右侧作等边三角形ADE．
1. （1）当AD平分∠BAC时，如图1，四边形ADCE是形；
2. （2）过E作EF⊥AC于F，如图2，求证：F为AC的中点；
3. （3）若AB=2，
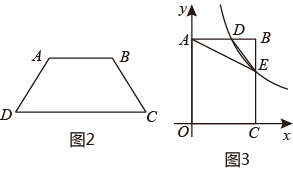
  ①当D为BC的中点时，过点E作EG⊥BC于G，如图3，求EG的长；
  ②点D从B点运动到C点，则点E所经过路径长为 ▲ ． (直接写出结果)
答案解析收藏纠错 + 选题
23. (2022·鄞州模拟) 如图1，平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 边上的点，连结 $\text{[math]}$ ，以 $\text{[math]}$ 为对称轴作 $\text{[math]}$ 的轴对称图形 $\text{[math]}$ .
1. （1）如图2，当点 $\text{[math]}$ 正好落在 $\text{[math]}$ 边上时，判断四边形 $\text{[math]}$ 的形状并说明理由；
2. （2）如图1，当点 $\text{[math]}$ 是线段 $\text{[math]}$ 的中点且 $\text{[math]}$ 时，求 $\text{[math]}$ 的长；
3. （3）如图3，当点 $\text{[math]}$ 三点共线时，恰有 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
24. (2021八下·北仑期末) 定义：只有三边相等的四边形称为准菱形.
1. （1）如图1，图形（填序号）是准菱形；
2. （2）如图2，四边形ABCD中，AB∥DC，∠B+∠D＝180°，AB＝AD，求证：四边形ABCD是准菱形；
3. （3）如图3，在平面直角坐标系xOy中，矩形OABC的边OA，OC分别落在y轴，x轴上，反比例函数y＝ $\text{[math]}$ （k＞0）的图象分别与边AB，BC交于点D，E.已知AD＝DE，△ADE的面积为10，AD：DB＝5：3，若点F是坐标平面上一点，四边形ADEF是准菱形，当准菱形ADEF面积最大时，求点F的坐标.
答案解析收藏纠错 + 选题
25. (2022·乐陵模拟) 在学完菱形后，某教学兴趣小组尝试利用手中的数学工具——三角板和圆规作出一个内角为60°的菱形，下面是他们探究过程中的讨论片段，请仔细阅读，并完成相应的任务．

小明：可以尝试利用含60°角的三角板和圆规作出菱形．如图①，将三角板ABC放置在图纸上、延长直角边BA，以点C为圆心、CA长为半径作弧，以点A为圆心、AC长为半径作弧，交BA的延长线于点E，交上弧于点D，连接CD，DE，则四边形ACDE即为所求作的菱形．

小华：我可以在不利用三角板的前提下，作出符合要求的菱形．如图②，作半圆O及其直径AB、分到以点OB为圆心、大于 $\text{[math]}$ 的长为半径作弧，两弧交于点MN，作直线MN交半径圆O于点C；以点C为圆心、OC长为半径作弧，交半圆O于点D，连接AD，CD，CO，则四边形AOCD即为所作的菱形．

任务：
1. （1）小明的做法中，判断四边形ACDE是菱形的依据可能是（填序号）
  ①四条边都相等的四边形是菱形；②对角线互相垂直的四边形是菱形
  ③有一组邻边相等的平行四边形是菱形；④对角线互相垂直的平行四边形是菱形
2. （2）请证明小明作出的图形四边形ACDE是菱形．
3. （3）你认为小华作出的四边形AOCD是有一个角为60°的菱形吗？请判断并说理由．
4. （4）如图③，小齐利用含45°角的三角板ABC和圆规构造了菱形ABMN，已知点P是线段MC上的一个点，AB＝10，当 $\text{[math]}$ 时，请直接写出点P到直线MN的距离．
答案解析收藏纠错 + 选题