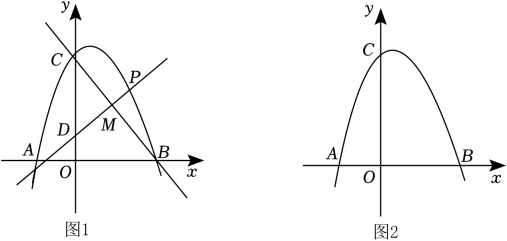
①求点和点
的坐标;
②若点 ,
分别为抛物线
和抛物线
上
,
之间的动点(点
,
与点
,
不重合),试求四边形
面积的最大值.
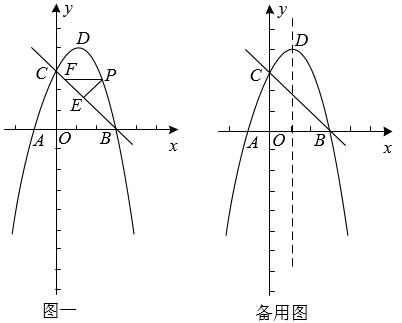

(Ⅰ)求该抛物线所表示的二次函数表达式;
(Ⅱ)若点P是抛物线上一动点(与点A不重合),过点P作PH⊥x轴于点H,与线段AB交于点M,是否存在点P使得点M是线段PH的三等分点?若存在,请求出点P的坐标:若不存在,请说明理由.
设 , 函数图象与
轴有两个不同的交点
,
, 若
,
两点均在原点左侧,探究系数
,
,
应满足的条件,根据函数图象,思考以下三个方面:
①因为函数的图象与轴有两个不同的交点,所以
;
②因为 ,
两点在原点左侧,所以
对应图象上的点在
轴上方,即
;
③上述两个条件还不能确保 ,
两点均在原点左侧,我们可以通过抛物线的对称轴位置来进一步限制抛物线的位置:即需
.
综上所述,系数 ,
,
应满足的条件可归纳为:
请根据上面阅读材料,类比解决下面问题:
若函数的图象在直线
的右侧与
轴有且只有一个交点,求
的取值范围.



①求 的最大值;
②连接 ,当
与
相似时,求点P的坐标.