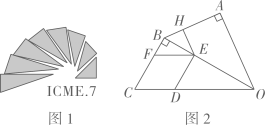

如图2,以△ABC的边AB和边AC为边长分别向外作正方形ABFH和正方形CED,过点F、E分别作BC的垂线段FM、EN,那么FM、EN、BC的数量关系是怎样?:说明理由.
如图3,在两平行线m、n之间有一正方形ABCD,已知点A和点C分别在直m、n上,过点D作直线l∥n∥m,已知l、n之间距离为l,l、m之间距离为2.直接出正方形的面积是.


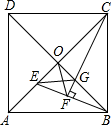
数学活动课上,同学们用尺规作图法探究在菱形内部作一点到该菱形三个顶点的距离相等.
【动手操作]如图,已知菱形 , 求作点E , 使得点E到三个顶点A , D , C的距离相等.小红同学设计如下作图步骤∶
①连接;
②分别以点A , D为圆心,大于的长为半径分别在
的上方与下方作弧:
上方两弧交于点M , 下方两弧交于点N , 作直线
交
于点E .
③连接 ,
, 则
.
方案设计 | 方案1 | 方案2 |
裁剪方案示意图 |
|
|
说明 | 图中的正方形AEFG和正方形MNPO四个顶点都在原四边形的边上 | |
测量数据 | AD=9dm,CD=2dm,AB=14dm,∠A=∠D=90°; | |
方案设计 | 方案1 | 方案2 |
裁剪方案示意图 |
|
|
说明 | 图中的正方形 | |
测量数据 |
| |
任务1:探寻边角 | 填空: | |
任务2:比较面积 | 计算或推理:正方形 | |
任务3:应用实践 | 若在 | |

图1 图2 图3 图4
如图,在△ABC中,点D、E分别是AB与AC的中点, 可以猜想:DE//BC且DE=
|

【定理证明】请根据教材内容,结合图①,写出证明过程.
∠ACB=80°,∠DAC=20°,直接写出LEFG的度数.
猜想 如图23.4.2,在
对此,我们可以用演绎推理给出证明.
|
【定理证明】
平行四边形的判定定理2 一组对边平行且相等的四边形是平行四边形.
我们可以用演绎推理证明这一结论.
已知:如图,在四边形中,AB
CD且
.
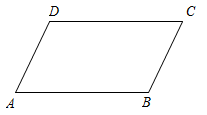
求证:四边形是平行四边形.
证明:连接 .
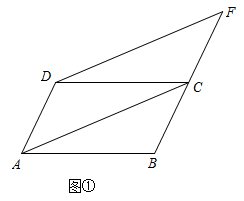

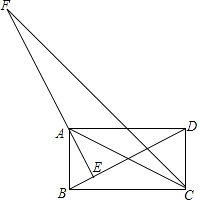
【探究展示】小明发现, , 并展示了如下的证明方法:
证明:∵ ,
∴ .
∵ ,
∴ .
∵四边形ABCD是矩形,
∴ .
∴ .
∵ ,
∴ .
∴ .
∵ ,
∴ . (依据)
其中两个角顶点重合于点
,
与
重合,已知
长
, 请你帮小都同学求出此时点
、
之间的距离;