题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

初中数学浙教版八下数学综合题优生特训7

更新时间：2022-06-11 浏览次数：36 类型：复习试卷

一、综合题

1. (2020八下·古冶期末) 如图，在平面直角坐标系中，点O是坐标原点，四边形 $\text{[math]}$ 是菱形，点A的坐标为 $\text{[math]}$ ，点C在x轴的正半轴上，直线 $\text{[math]}$ 交y轴于点M， $\text{[math]}$ 边交y轴于点H，连接 $\text{[math]}$ ．
1. （1）菱形 $\text{[math]}$ 的边长是；
2. （2）求直线 $\text{[math]}$ 的解析式；
3. （3）动点P从点A出发，沿折线 $\text{[math]}$ 方向以2个单位/秒的速度向终点C匀速运动，设 $\text{[math]}$ 的面积为 $\text{[math]}$ ，点P的运动时间为t秒，当点P在 $\text{[math]}$ 边上运动时，求S与t间的函数关系式．
答案解析收藏纠错 + 选题
2. (2020八下·阜平期末) 如图，在平面直角坐标系中，直线 $\text{[math]}$ ： $\text{[math]}$ 分别与x轴、y轴交于点B、C，且与直线 $\text{[math]}$ ： $\text{[math]}$ 交于点A.
1. （1）分别求出点A、B、C的坐标；
2. （2）若D是线段 $\text{[math]}$ 上的点，且 $\text{[math]}$ 的面积为12，求直线 $\text{[math]}$ 的函数表达式；
3. （3）在（2）的条件下，设P是射线 $\text{[math]}$ 上的点，在平面内里否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
3. (2020八下·无为期末) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点E，交 $\text{[math]}$ 的延长线于F，以 $\text{[math]}$ 为邻边作平行四边形 $\text{[math]}$ 。
1. （1）证明平行四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ，连结 $\text{[math]}$ ，①求证： $\text{[math]}$ ；②求 $\text{[math]}$ 的度数；
3. （3）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，M是 $\text{[math]}$ 的中点，求 $\text{[math]}$ 的长。
答案解析收藏纠错 + 选题
4. (2020八下·瑶海期末) 如图1，正方形ABCD的顶点A、D分别在平行线l₁、l₂上，由B、D向l₁作垂线，垂足分别为M、N．
1. （1）求证：AM=DN；
2. （2）如图2，正方形AEFG的顶点E在直线l₂上，过点F、C分别作l₂的垂线段FP、CQ，求证：FP+CQ=DE；
3. （3）如图3，正方形AEFG的顶点A、G在直线l₁上，顶点E、F在直线l₂上，连接BG并延长交l2于点R，若∠BRD=30°，AE= $\text{[math]}$ ，求AB．
答案解析收藏纠错 + 选题
5. (2020八下·江干期末) 如图，已知在矩形ABCD中，点E在AB边上，F在CE边上，且∠ACD＝∠DAF.
1. （1）当∠CAF＝30°时，求矩形的长宽之比；
2. （2）若∠CAF＝∠ECB，请回答下列问题；
  ①设∠ACE＝x，∠CAF＝y，求y关于x的表达式；
  
  ②若EB＝1，求CF的长.
答案解析收藏纠错 + 选题
6. (2020八下·南县期末) 如图，在平面直角坐标系中，已知点A（－6，0），B（0，8），点C为OB的中点，点D在第二象限，四边形AOCD为矩形，直线AB交DC于点E.
1. （1）求直线AB的解析式及点E的坐标；
2. （2）动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点N从点A出发沿线段AO以每秒2个单位长度的速度向终点O运动，当其中一点到达终点时，两点同时停止运动. 连接NP，设点P的运动时间为 $\text{[math]}$ 秒.
  ①当 $\text{[math]}$ 为何值时，四边形ANPE 为平行四边形？
  
  ②当 $\text{[math]}$ 为何值时，四边形ANPD 为矩形？
答案解析收藏纠错 + 选题
7. (2020八下·金牛期末) 如图1，在平面直角坐标系中，直线y＝ $\text{[math]}$ x+n分别与x轴、y轴交于点A、B，且点A的坐标为（4，0），点C为线段AB的中点．
1. （1）求点B的坐标；
2. （2）点P为直线AB上的一个动点，过点P作x轴的垂线，与直线OC交于点Q，设点P的横坐标为m，△OPQ的面积为S，求S与m的函数解析式；
3. （3）当点P在直线AB上运动时，在平面直角坐标系内是否存在一点N，使得以O，B，P，N为顶点的四边形为矩形，若存在，求出N点的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
8. (2020八下·重庆期末) 如图，平行四边形ABCD中AB∥CD，AD∥BC，点G是线段BC的中点，点E是线段AD上的一点，点F是线段AB延长线上一点，连接DF，且∠ABE＝∠CDG＝∠FDG.
1. （1） ∠A＝45°，∠ADF＝75°， $\text{[math]}$ ，求线段BC的长；
2. （2）求证：AB＝BF+DF .
答案解析收藏纠错 + 选题
9. (2020八下·万州期末) 已知如图1，四边形 $\text{[math]}$ 是正方形， $\text{[math]}$ .
1. （1）如图1，若点 $\text{[math]}$ 分别在边 $\text{[math]}$ 上，延长线段 $\text{[math]}$ 至 $\text{[math]}$ ，使得 $\text{[math]}$ ，若 $\text{[math]}$ 求 $\text{[math]}$ 的长；
2. （2）如图2，若点 $\text{[math]}$ 分别在边 $\text{[math]}$ 延长线上时，求证： $\text{[math]}$
3. （3）如图3，如果四边形 $\text{[math]}$ 不是正方形，但满足 $\text{[math]}$ 且 $\text{[math]}$ ，请你直接写出 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
10. (2020八下·涪陵期末) 如图，在菱形ABCD中，∠A＝60°，E为菱形ABCD内对角线BD左侧一点，连接BE、CE、DE.
1. （1）若AB＝6，求菱形ABCD的面积；
2. （2）若∠BED＝2∠A，求证：CE＝BE+DE.
答案解析收藏纠错 + 选题
11. (2022八下·河东期中) 如图l，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AM $\text{[math]}$ BE，垂足为M，AM交BD于点F.
1. （1）求证：OE=OF；
2. （2）如图2，若点E在AC的延长线上，AM $\text{[math]}$ BE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗.如果成立，请给出证明；如果不成立，请说明理由.
答案解析收藏纠错 + 选题
12. (2020八下·滨江期末) 矩形ABCD中，AB=3，BC=4.点E，F在对角线AC上，点M，N分别在边AD，BC上.
1. （1）如图1，若AE=CF=1，M，N分别是AD，BC的中点.求证：四边形EMFN为矩形.
2. （2）如图2，若AE=CF=0.5， $\text{[math]}$ ，且四边形EMFN为矩形，求x的值.
答案解析收藏纠错 + 选题
13. (2020八下·高邮期末) 如图，已知正方形ABCD的边长为2，两条对角线相交于点O，以O为顶点作正方形OEFG，将正方形OEFG绕点O旋转.
1. （1）旋转过程中，正方形OEFG与正方形ABCD重叠部分的面积为
2. （2）连接BG，EC，延长EC交BG于点H，判断EC与BG的位置关系，并说明理由；
3. （3）连接DE，当以B、D、E、C为顶点的四边形是平行四边形时，求点D到OE的距离
答案解析收藏纠错 + 选题
14. (2020八下·牡丹江期末) 在菱形 $\text{[math]}$ 中，点E为边 $\text{[math]}$ 的中点， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，垂足为点G．
1. （1）如图①，求证： $\text{[math]}$ ；
2. （2）如图②，如图③，请分别写出线段 $\text{[math]}$ 之间的数量关系，不需要证明；
3. （3）在（1）（2）的条件下，若菱形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，菱形 $\text{[math]}$ 的周长为 $\text{[math]}$ ，四边形 $\text{[math]}$ 的面积为，线段 $\text{[math]}$ 的长为．
答案解析收藏纠错 + 选题
15. (2020八下·阳西期末) 如图，在菱形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.
1. （1）求证：四边形AMDN是平行四边形；
2. （2）当AM的值为时，四边形AMDN是矩形；
3. （3）若 $\text{[math]}$ ，求证：四边形AMDN是菱形.
答案解析收藏纠错 + 选题
16. (2022八下·晋安期末) 如图
1. （1）如图1所示，已知正方形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点，且 $\text{[math]}$ .求证： $\text{[math]}$ ；
2. （2）如图2所示，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ 是 $\text{[math]}$ 上一点，如果 $\text{[math]}$ ，请利用（1）中的结论证明： $\text{[math]}$ .
答案解析收藏纠错 + 选题
17. (2020八下·玉州期末) 如图，在平行四边形 $\text{[math]}$ 中，点P是 $\text{[math]}$ 边上一点（不与A，B重合）， $\text{[math]}$ ，过点P作 $\text{[math]}$ ，交 $\text{[math]}$ 边于点Q，连结 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是矩形；
2. （2）在（1）的条件下，当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
18. (2020八下·厦门期末) 如图正方形ABCD，点E、G、H分别在AB、AD、BC上，DE与HG相交于点O.
1. （1）如图1，当∠GOD=90°，
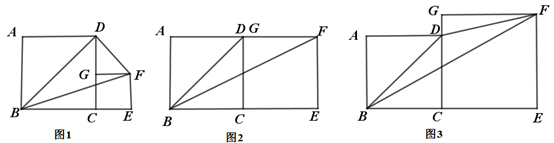
  ①求证：DE=HG
  
  ②平移图1中线段GH，使G点与D重合，H点在BC延长线上，连接EH，取EH中点P，连接PC，如图2，求证：BE= $\text{[math]}$ PC；
2. （2）如图3，当∠GOD=45°，边长AB=4，HG= $\text{[math]}$ ，则DE的长为（直接写出结果）．
答案解析收藏纠错 + 选题
19. (2022八下·泉州期末) 如图，在矩形ABCD中，AD＝nAB，E，F分别在AB，BC上．
1. （1）若n＝1，AF⊥DE．
  ①如图1，求证：AE＝BF；
  
  ②如图2，点G为CB延长线上一点，DE的延长线交AG于H，若AH＝AD，求证：AE+BG＝AG；
2. （2）如图3，若E为AB的中点，∠ADE＝∠EDF．则 $\text{[math]}$ 的值是（结果用含n的式子表示）．
答案解析收藏纠错 + 选题
20. (2020八下·海沧期末) 在平面直角坐标系中，点O为坐标原点，点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ 在第一象限内．
1. （1）若点C在直线 $\text{[math]}$ 上，求点 $\text{[math]}$ 的值；
2. （2）若直线AB的解析式为： $\text{[math]}$ ，求证：四边形OABC为菱形；
3. （3）直线AC与直线OB相交于点 $\text{[math]}$ ，则在射线OB上是否存在点G使得 $\text{[math]}$ 是直角三角形．若存在请求出点G坐标，若不存在，请说明理由．
答案解析收藏纠错 + 选题
21. (2020八下·博白期末) 如图，平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 是边 $\text{[math]}$ 上的动点， $\text{[math]}$ 的延长线与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，连接CE， $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2） ①当 $\text{[math]}$ 的长为多少时，四边形 $\text{[math]}$ 是矩形；
  ②当 $\text{[math]}$ $\text{[math]}$ 时，四边形 $\text{[math]}$ 是菱形，（直接写出答案，不需要说明理由）.
答案解析收藏纠错 + 选题
22. (2020八下·西乡塘期末) 如图，在菱形ABCD中，AB＝2cm，∠ADC＝120°.动点E、F分别从点B、D同时出发，都以0.5cm/s的速度向点A、C运动，连接AF、CE，分别取AF、CE的中点G、H.设运动的时间为ts （0＜t＜4）.
1. （1）求证：AF∥CE；
2. （2）当t为何值时，△ADF的面积为 $\text{[math]}$ cm²；
3. （3）连接GE、FH.当t为何值时，四边形EHFG为菱形.
答案解析收藏纠错 + 选题
23. (2020八下·西乡塘期末) 平面直角坐标系中，点A、点B的坐标分别是（﹣4，0）、（0，2）.
1. （1）求直线AB的解析式；
2. （2）如图1，点P是直线AB上一点，若△AOP的面积是△AOB面积的2倍，求点P的坐标；
3. （3）若点P满足（2）的条件，且在第一象限内，如图2.点M是y轴负半轴上一动点，连接PM，过点P作PN⊥PM，交x轴于点N.当点M运动时，（ON﹣OM）的值是否为定值？若是，请求出它的值；若不是，请说明理由.
答案解析收藏纠错 + 选题
24. (2020八下·攀枝花期末) 如图，菱形ABCD的边长为12cm，∠A＝60°，动点P从点A出发，沿着线路AB—BD做匀速运动，动点Q从点D同时出发，沿着线路DC－CB－BA做匀速运动.
1. （1）求BD的长.
2. （2）已知动点P运动的速度为2cm/s，动点Q运动的速度为2.5cm/s.经过12秒后，P、Q分别到达M、N两点，试判断△AMN的形状，并说明理由.
3. （3）设问题（2）中的动点P、Q分别从M、N同时沿原路返回，动点P的速度不变，动点Q的速度改变为acm/s，经过3秒后，P、Q分别到达E、F两点，若△BEF为直角三角形，试求a值.
答案解析收藏纠错 + 选题
25. (2020八下·南部期末) 如图，在直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ 于H.
1. （1）判断 $\text{[math]}$ 的形状，并说明理由.
2. （2）求点D的坐标.
3. （3）若P是 $\text{[math]}$ 上的动点，当 $\text{[math]}$ 的周长最小时，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
26. (2022八下·虞城期末) 如图，在平面直角坐标系中，O为原点，已知直线y＝﹣ $\text{[math]}$ x+4与x轴交于点A，与y轴交于点B．
1. （1）点A的坐标为，点B的坐标为；
2. （2）如图①，若点M（x，y）在线段AB上运动（不与端点A、B重合），连接OM，设 $\text{[math]}$ 的面积为S，写出S关于x的函数解析式，并写出自变量x的取值范围；
3. （3）如图②，点C在直线AB上，若四边形OADC是菱形，求菱形对角线OD的长．
答案解析收藏纠错 + 选题
27. (2020八上·龙泉驿期末) 如图，直线y=﹣2x+8分别交x轴，y轴于点A ， B ，直线y $\text{[math]}$ x+3交y轴于点C ，两直线相交于点D ．
1. （1）求点D的坐标；
2. （2）如图2，过点A作AE∥y轴交直线y $\text{[math]}$ x+3于点E ，连接AC ， BE ．求证：四边形ACBE是菱形；
3. （3）如图3，在（2）的条件下，点F在线段BC上，点G在线段AB上，连接CG ， FG ，当CG=FG ，且∠CGF=∠ABC时，求点G的坐标．
答案解析收藏纠错 + 选题
28. (2020八下·海勃湾期末) 正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上，分别连接BD、BF、FD，得到 BFD．
1. （1）在图1、图2、图3中，若正方形CEFG的边长分别为1、3、4，且正方形ABCD的边长均为3，请通过计算填写下表：
  
  正方形CEFG的边长
  
  1
  
  3
  
  4
  
  BFD的面积
2. （2）若正方形CEFG的边长为a，正方形ABCD的边长为 $\text{[math]}$ ，猜想 $\text{[math]}$ 的大小，并结合图3证明你的猜想.
答案解析收藏纠错 + 选题
29. (2020八下·汽开区期末) 如图，在△ABC中，点D在BC上， $\text{[math]}$ ，点E为AD的中点，过点A作AF∥BC交BE的延长线于点F ，连结CF．
1. （1）求证：AD=AF．
2. （2）当点D为BC中点时，
  ①∠ACB=度时，四边形ADCF为正方形．
  
  ②连结DF，当∠ACB=度时，四边形ABDF为菱形．
答案解析收藏纠错 + 选题
30. (2020八下·吉林期末) 如图，在 $\text{[math]}$ 中，对角线AC，BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG=AE，连接CF，CG．
1. （1）求证： $\text{[math]}$ ；
2. （2）若AB= $\text{[math]}$ ，AC=10，BD=12．直接写出四边形EGCF的面积．
答案解析收藏纠错 + 选题

试卷信息