
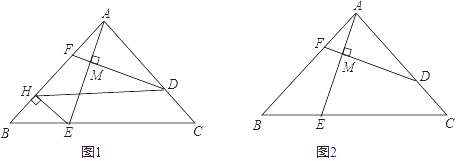
①求证:四边形DHEC是平行四边形;
②若m= ,求证:AE=DF;


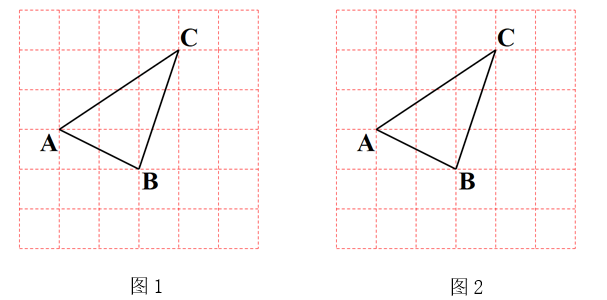
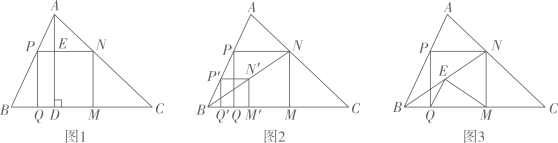
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
推理:证明图2中的四边形 是正方形.


如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作,先在AB上任取一点 ,画正方形
,使
,
在
边上,
在△
内,然后连结
并延长交
于点N,画
⊥
于点
,
⊥
交
于点
,
⊥
于点
,得到四边形P
.
推理:证明图2中的四边形 是正方形.